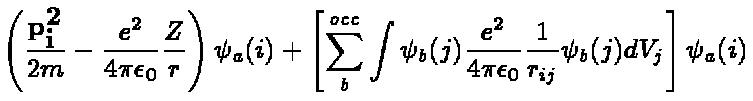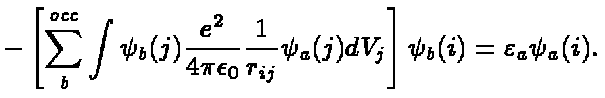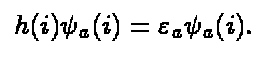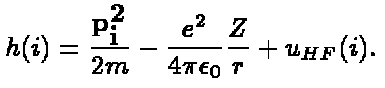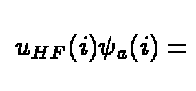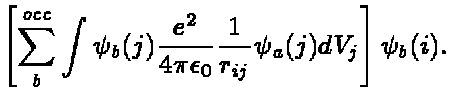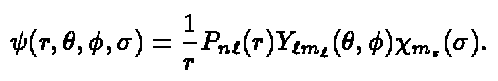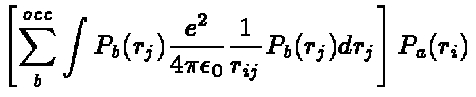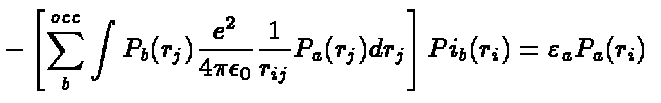Hartree-Fock equations - The Formulae
Oktober - November 1995 version
Minimizing the energy with respect
to changes in the Slater determinant leads to the
Hartree-Fock equations
(6) 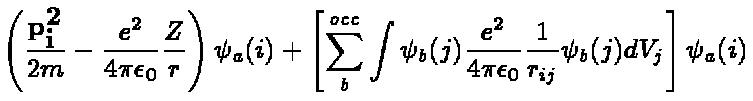
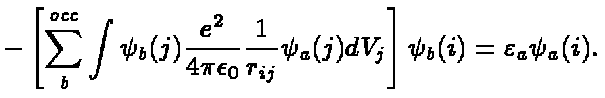
As before a and b denote
the quantum numbers necessary to specify a
single electron state. The sum over b runs over all occupied states.
Although the expression looks complicated it is just an eigenvalue equation
of the form
(7) 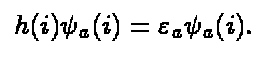
where h is
(8) 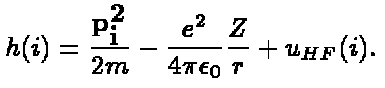
The last term, u HF (i) is called the
Hartree-Fock potential.
From the above we can see that its effect on $\psi_a(i)$ is
(9)
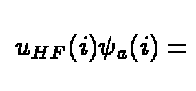

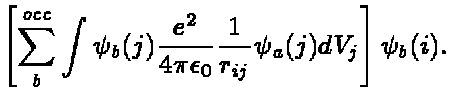
Due to the presence of the last term, the exchange potential , the
potential is non-local. The exchange term is a consequence of
the Pauli principle and the requirement of antisymmetric wave functions.
In the general case the
Hartree-Fock equations given in Eq.(eq:hf), are
hard to solve. In practice a few other
restrictions are thus imposed on the spin-orbitals, psi . The first
restriction is the requirement that the spin-orbital can be separated into one
spin and one orbital part. The second restriction is
that we assume that the psi's are solutions to a spherical
symmetric potential. This later restriction is called the
central field approximation and it make possible a separation of the
orbital part of the wave function into one radial and one angular part.
For a closed shell system, where the total spin and angular momentum is
zero, the system is indeed spherical symmetric and that restriction is
automatically fulfilled.
We can now write the spin-orbital as a product of the radial, the angular
and the spin part
(10) 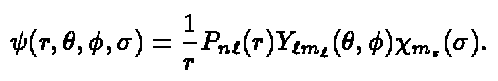
The Y l m 's are spherical harmonics and the Hartree-Fock
equations can now be simplified to
the radial Hartree-Fock equations
(11)

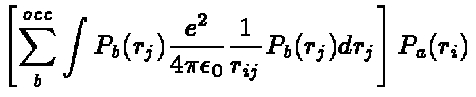
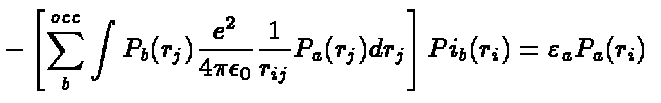
which can be solved to obtain the radial functions, P .
As can be seen from the above equations,
the equation for Pa depends on
the radial functions for all the other electrons.
Because of that one uses an iterative scheme. The starting point is
an approximative description of the single particle functions, P(r) . It
could be hydrogen-like functions, but usually some better approximation is
used. With these starting functions the Hartree-Fock potential is
constructed and the eigenvalue equation, Eq.(7), is solved.
Then a
new set of single-particle functions are obtained and a new
Hartree-Fock potential is
constructed and again the eigenvalue equation,Eq.(7),
is solved. This
is done over and over again until the radial functions as well
as the energy eigenvalues are stable.
We call this a self-consistent field
method.
The Herman-Skillman program which we use, is not of Hartree-Fock,
but of Hartree type. That means that the
exchange potential term (the non-local one), is not
included.
Instead, it is simulated by a statistical exchange term.
One consequenceis that there is only one
average potential for all orbitals considered.
About the Herman-Skillman
Clicking on the formula will bring you it's latex source