2010.10.14 previous lecture
note
2010.10.21 next lecture note
Hartree-Fock - Derivation + DFT + Configuration Interaction
Configuration - how are the electrons distributed over the states.
For the ground state - the natural configuration is the N lowest energy
states
But there can be a different configuration - e.g. one electron is in a
higher
state than it should be
Why is this relevant - see below
Configuration metaphore - chesboard (starting configuration - the king
and queen
and the bishops .... the towers ... not much exchange symmetry there
... )
 1-intro.png
1-intro.png
We also revisited the Lagrange Multiplier - the paroboloid
- minimum on a LINE
(the limiting surface is an inclied plane (Schiefe Ebene in German I hope -
skråplanet in Norwegian) )
There it is easy to see how the minimum slides along the inclied plane
until it hits the limiting line g(x,y)=0 ....
We looked back at last lecture - the single-particle operators and
the pairs
 11-Counting_Lithium.png
11-Counting_Lithium.png
Deriving hartree fock by the variational prescription revisited
See the Schrödinger equation from variational "principle" ... last
time
 2-derive-H.F.-.png
2-derive-H.F.-.png
the Schrödinger equation from variational "principle" ... last
time ... is repeated here in the bottom
One more visit to counting the terms
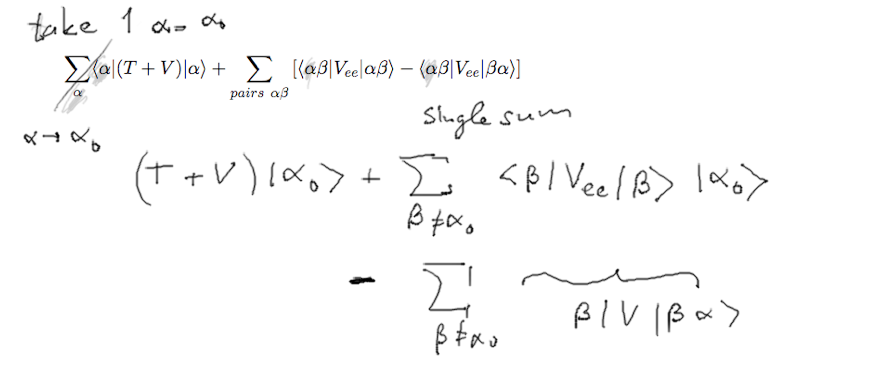 3-derive-H.F.-sin-particle.png
3-derive-H.F.-sin-particle.png
Taking the pairs - and doing the analogue of the Schrödinger
equation from variational "principle"
- in practice it meant slashing away the Dirac < bra
| from all the < a |
O | b >
First we get back the Hartree terms
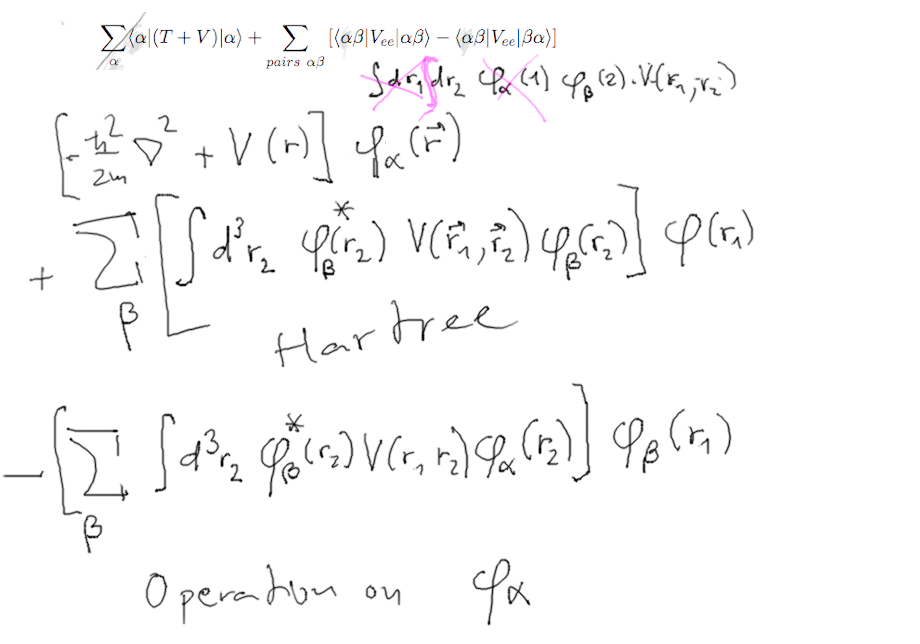 4-derive-H.F.-two-particle.png
4-derive-H.F.-two-particle.png
But the last exchange term is quite a different kind of animal ...
When we look at it we discover that it behaves as a NON-LOCAL OPERATOR
 5-derive-H.F.-exchange.png
5-derive-H.F.-exchange.png
Above is the explicit form of the non-local exchange interaction
 6--H.F.-exchange.png
6--H.F.-exchange.png
It is in this case a demonstration of the "exclusion" principle in
space
 7-nonlocal-exchange.png
7-nonlocal-exchange.png
... often talked about as a repulsion "hole"
 8-nonlocal-DFT.png
8-nonlocal-DFT.png
Link to Schrodinger Inc: http://www.schrodinger.com/
in particular: Jaguar: http://www.schrodinger.com/products/14/7
(this last link might change next year, but JAGUAR is our
desired product)
Here we look at an important question:
we obtain the Hartree-fock Lagrange multipliers = SIngle electron
selfconsistent energies
Is the total electron energy equal to the sum - the answer is NO!
It is related to
Koopmans' theorem
http://en.wikipedia.org/wiki/Koopmans%27_theorem
 81-sum-orbital-energies.png
81-sum-orbital-energies.png
You must subtract the pair interaction, because it is counted twice
Expansion in a basis - we have some notes in the PHYS208 notes: web.ift.uib.no/AMOS/PHYS208/2010.10.18/index.html#expand
Now we come back to the Configuration Interaction
 8-config-interaction.png
8-config-interaction.png
We apply the expansion twice
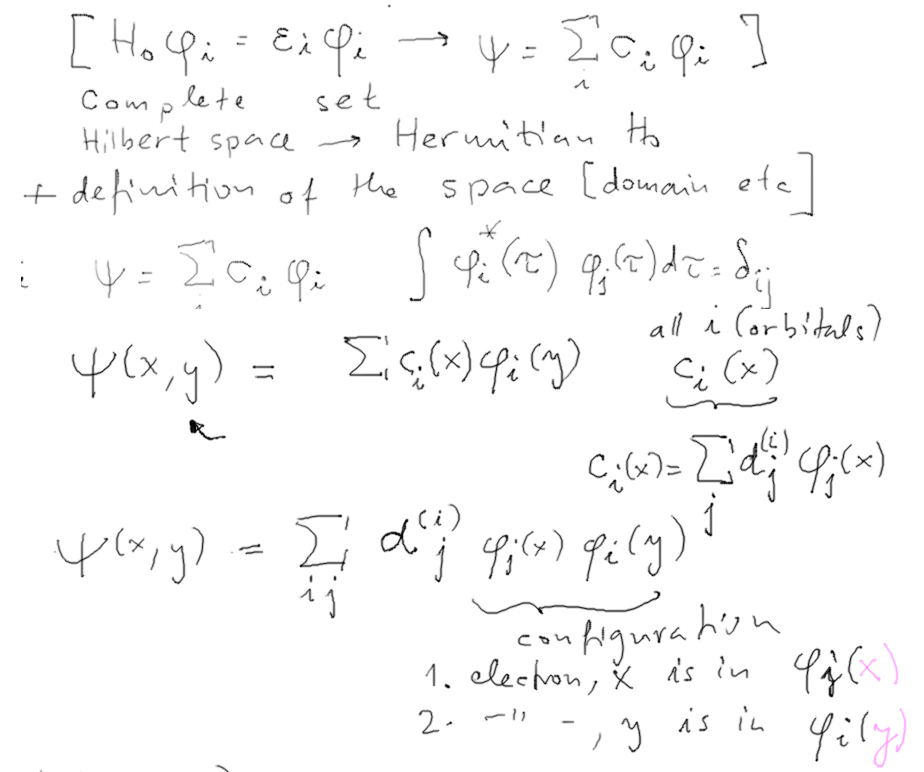 9-config-interaction.png
9-config-interaction.png
And here three times - and so on
So expansion over configurations follows naturally from this
 a-config-interaction.png
a-config-interaction.png
AND THE CONFIGURATION INTERACTION thus means removing the INDEPENDENT
PARTICLES feature
Thus CONFIGURATION
INTERACTION means ELECTRON
CORRELATIONS
Link to diagonalization in PHYS208 notes: http://web.ift.uib.no/AMOS/PHYS208/2010.10.18/index.html#diag
2010.10.14 previous lecture
note
2010.10.21 next lecture note
 1-intro.png
1-intro.png  11-Counting_Lithium.png
11-Counting_Lithium.png  2-derive-H.F.-.png
2-derive-H.F.-.png 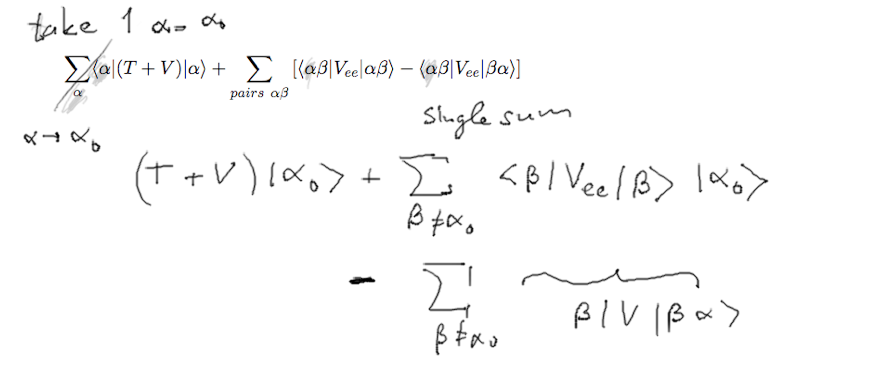 3-derive-H.F.-sin-particle.png
3-derive-H.F.-sin-particle.png 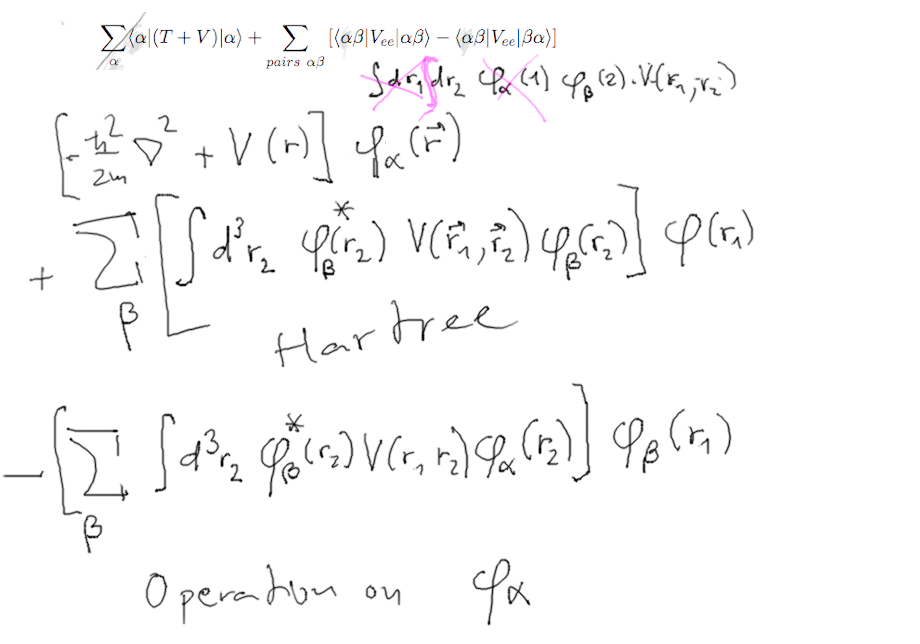 4-derive-H.F.-two-particle.png
4-derive-H.F.-two-particle.png  5-derive-H.F.-exchange.png
5-derive-H.F.-exchange.png  6--H.F.-exchange.png
6--H.F.-exchange.png  7-nonlocal-exchange.png
7-nonlocal-exchange.png  8-nonlocal-DFT.png
8-nonlocal-DFT.png  81-sum-orbital-energies.png
81-sum-orbital-energies.png  8-config-interaction.png
8-config-interaction.png 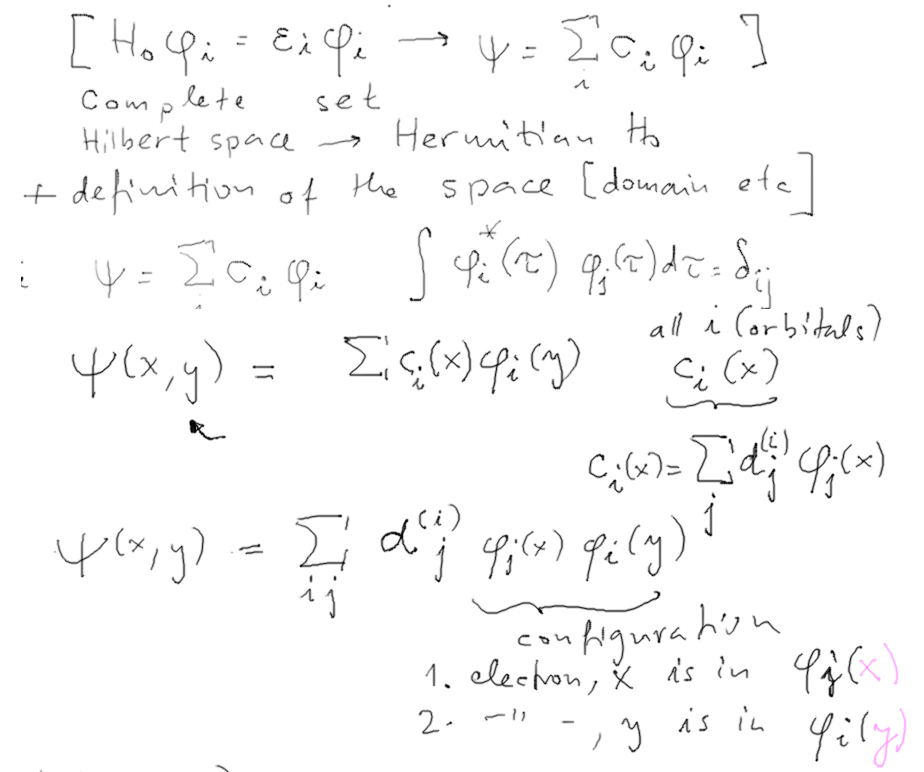 9-config-interaction.png
9-config-interaction.png  a-config-interaction.png
a-config-interaction.png