2010.09.28 previous lecture note                                                  2010.10.19 next lecture note
Self-consistent field - towards Hartree- Fock method 
    

Files to work on 

Self-consistent field program ( FORTRAN, 1963 Herman & Skillman )

fortran3.zip       The collection of files for Mac, Windows and Unix
         SCF-work - Hartree (1995 Stockholm Course)
Oct 14 18:03
      
1331335 Bytes
Many_Electrons_Atoms_2008.pdf      The text used in the lecture
 Dec 1 2008 815179 Bytes

Fortran code         SCF-work - Hartree (1995 Stockholm Course)

Mac and Windows  - executable code in the above zip-file
Unix-Linux Users (including Mac Users - g95 for Mac available) 
Use the     herman3.f       and      radhyd3.f      FORTRAN SOURCES
compile by
gfortran -o herman3   herman3.f      (  replace gfortran   by the compiler you have,
                                                            e.g. g95  g77 ......  fortran .....   )
and execute as described in the course
SCF-work - Hartree (1995 Stockholm Course)
but nowadays with

./herman3 < in13                     ( dot slash before the code name; security is the reason .... )
on windows

cd   D:\some_data\your_names\fortran3                (or where is your working directory wiyh fortran3

herman3 < in13      in the com.exe  window           (cd   to the correct directory first )

Pictures and notes

Ionization potential  - is the apparent (over-all) binding energy of the least bound electron.
I say apparent - because the "binding" can be larger - but the repulsion reduces it.
Experimentally it is exactly defined - the energy needed to free one electron
(except, it should be called ionization energy and not potential - historical reasons (why do you think) )
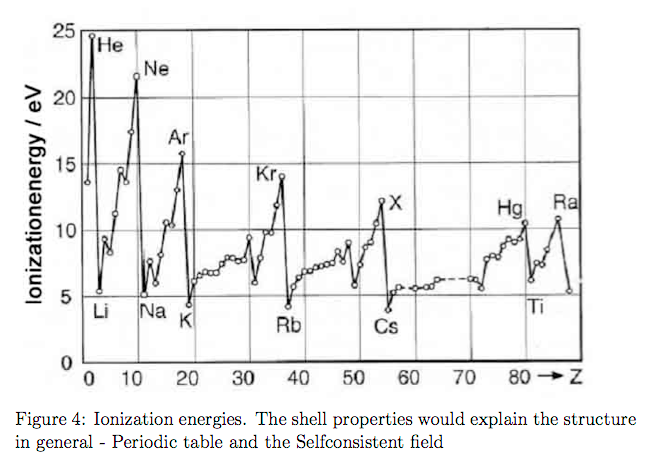0-Ionization-potentials.png
Here we can have another homework or puzzle:
The binding energy should increase with Z*Z roughly - or perhaps a little bit like Z (discuss it)
so why exactly do we have the "back jumps down at 11, 19, 37 .....

These are the chemistry facts; configurations, Ionization potentials (energies)

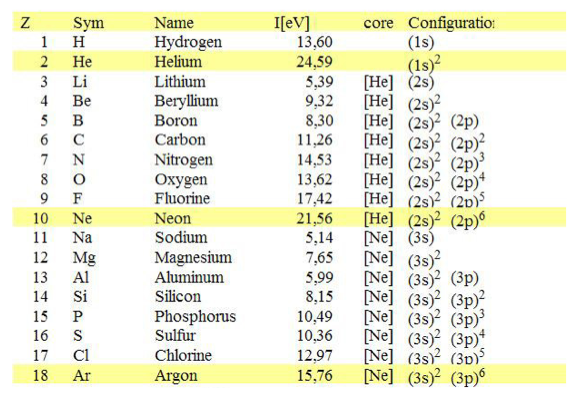1-Z=1_to_Z=18.png
                                                                                                                                      Nickel should have been Noble gas!
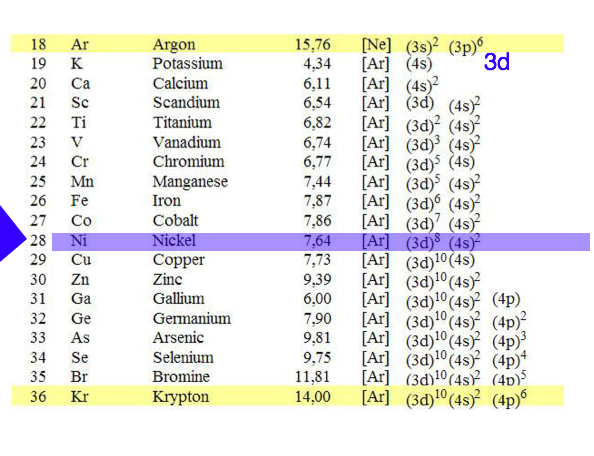2-Z=18_to_Z=36.png

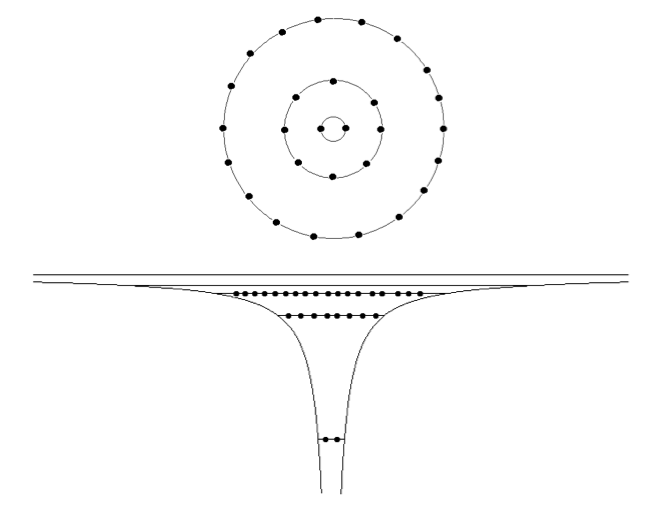3-Aufbau_Principle.png

3-magic-numbers_NxN.png
EXPLAIN the 4s - 3d and the following levels discrepancy

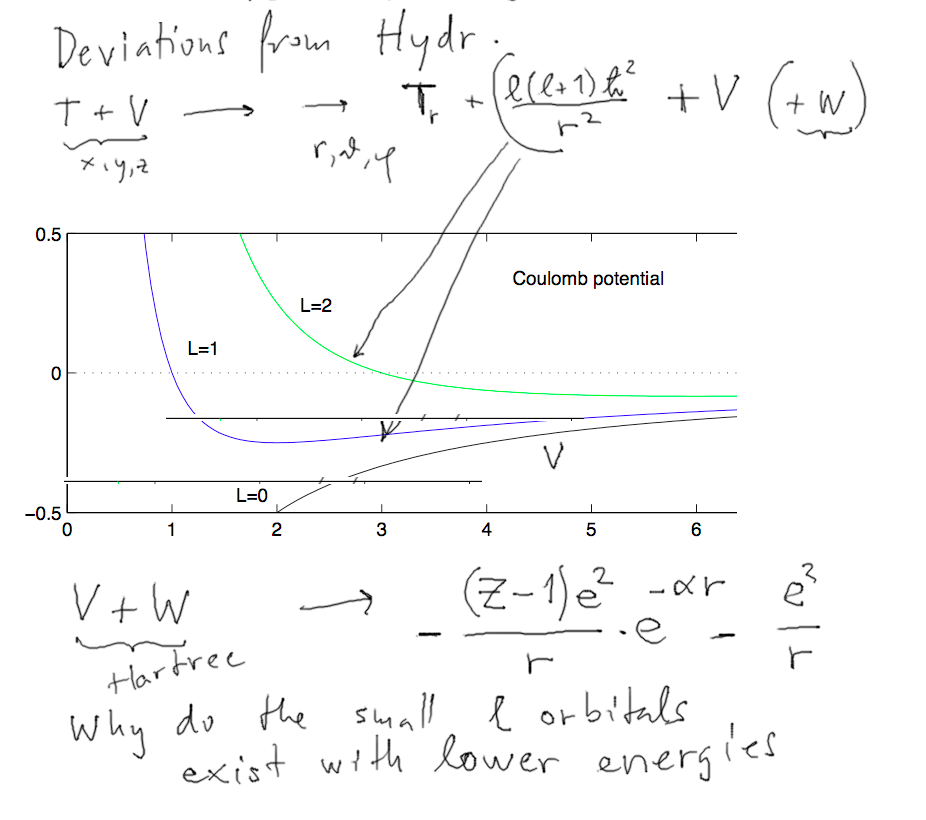4-explain-why-centrifugal.png

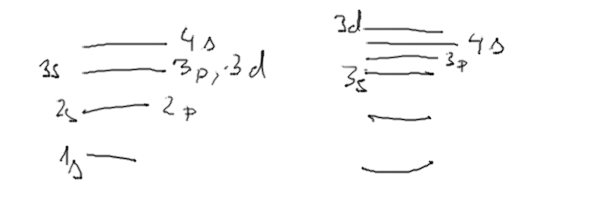5__1s_2s_2p_3s_3p_4s_3d.png
Theoretical description
Slater determinant - product functions with built in ANTISYMMETRIZATION
6-Slater_determinant.png
What evaluates to   -  The  expectation value of energy     <  Phi  |    H   |  Phi  >

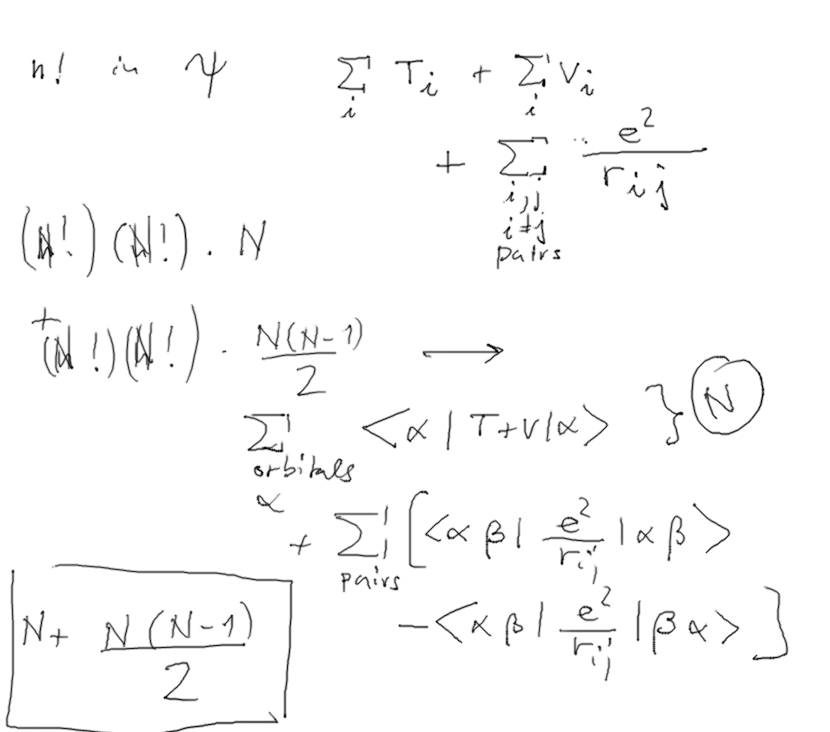7-Energy_in_Slater_determinant.png

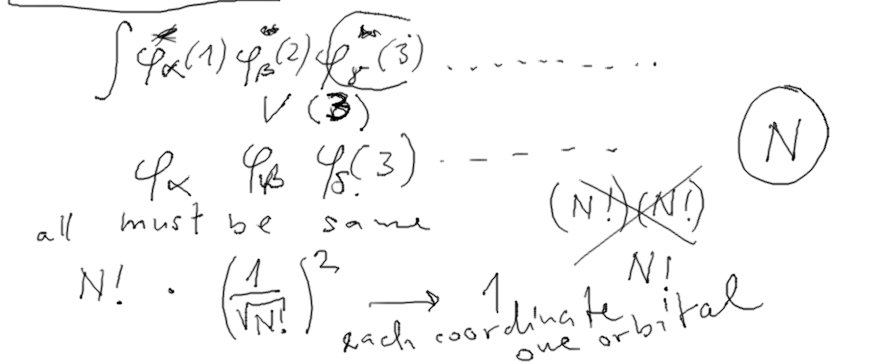8-counting.png

9-Result_Slater.png

9b-Result_Slater.png
Schrödinger equation can only be 'obtained' from variational method  if we use
the minimum with constraint - i.e. the method of Lagrange multipliers
a-Schrodinger.png
The method of Lagrange multipliers  explained
in 2-variable case - the functions are 2 surfaces; the one defining the constraint -
a curve in the plane - is always ZERO at the constrained curve, multiplied by any lambda
(any multiplier). Now you combine the two surfaces by changing lambda until some
minimum falls on the constraint curve g(x,y)=0 .....

It is easy to illustrate by taking the "curve" defined by g(x,y) as a straight line (linear g(x,y) )
the surface defined by g( )  is an inclined plane.

Draw a parabola over an inclined line and let the incline change - the position
of minimum is 'obviously' changing ....
b-variation-Schrodinger.png
The variational method is to be used for the derivation of the Hartree - Fock method
b-variation-HARTREE.png


2010.09.28 previous lecture note                                                  2010.10.19 next lecture note