Previous lecture 2010.11.02
to index
Next lecture 2010.11.16
Quantizing extended
system,
04.11.2010
Creation+Annihilation Operators,
Density of
states
Included below:
Lagrange function and Hamilton function for a charged particle in el mag field
charge-in-elmag-derivation-jpg/ Here are preliminary pictures of pages ....

1-quantum-theory-of-extended-systems.png
Classical mechanics - Finding
eigenmodes
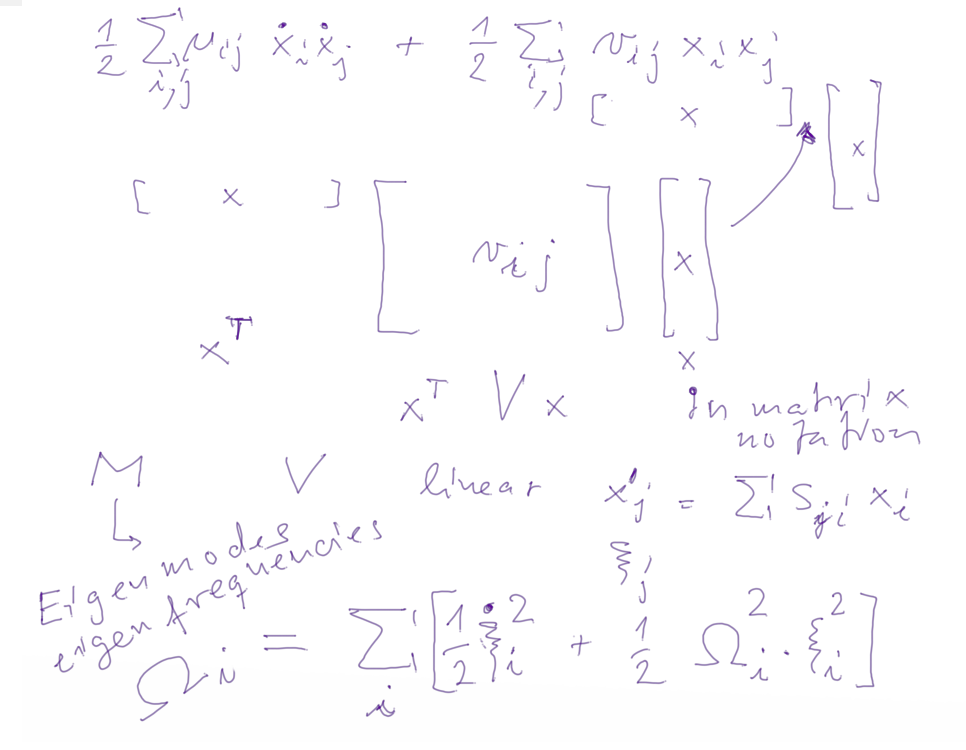
2-eigenmodes-of-coupled-oscillating...png
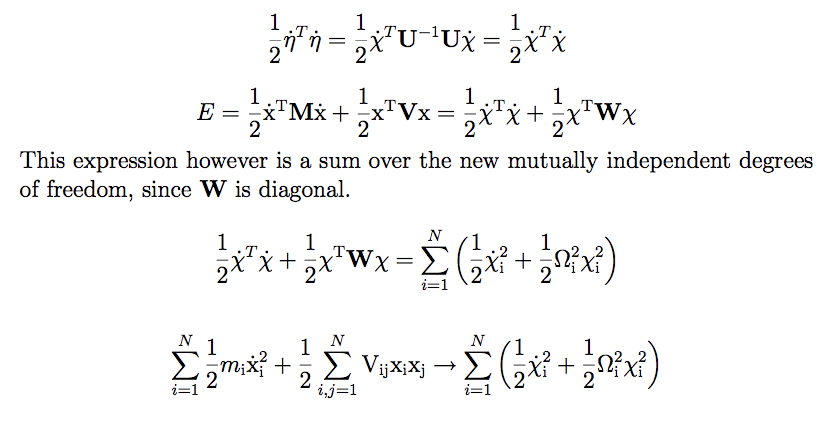 3-eigenmodes-of-coupled-oscillating...png
3-eigenmodes-of-coupled-oscillating...png
Quantum mechanics - for each independent Harmonic Oscillator
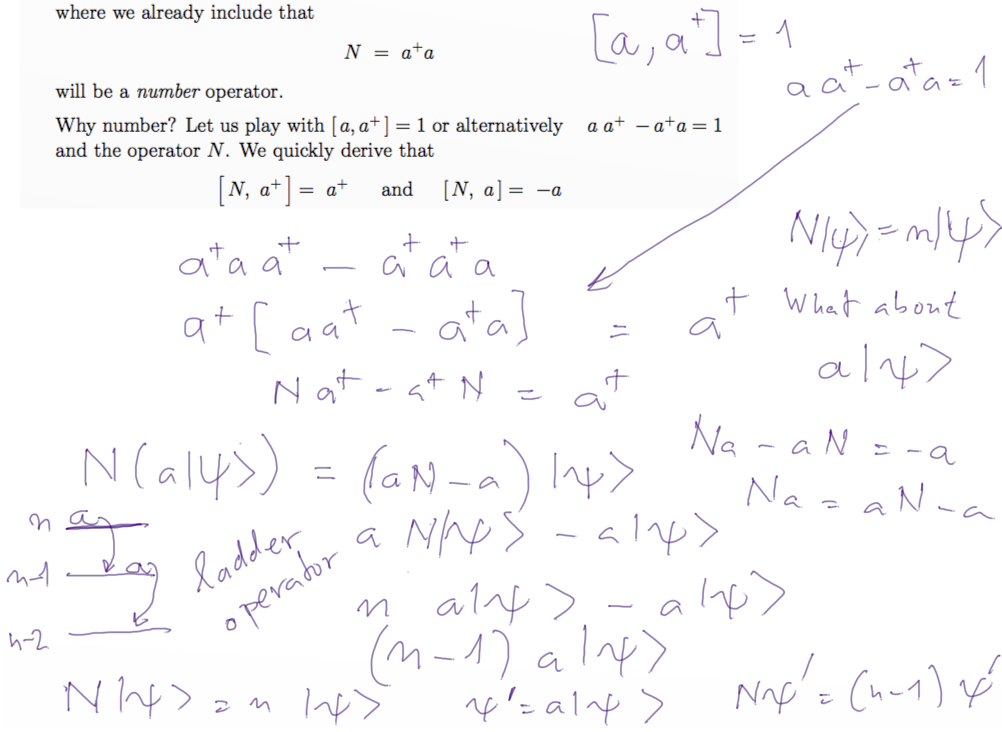 5-QM-harm-oscillator.png
5-QM-harm-oscillator.png
EXTRA
BONUS: Solve Schrödinger Equation as a 1. order equation -
see below
 6-extra-QM-harm-oscillator.png
6-extra-QM-harm-oscillator.png
 7-Fields.png
7-Fields.png
Electro-magnetic fields;
ENERGY
 a1-energy-inmagn-field.png
a1-energy-inmagn-field.png
Quantization of El-Mag Field
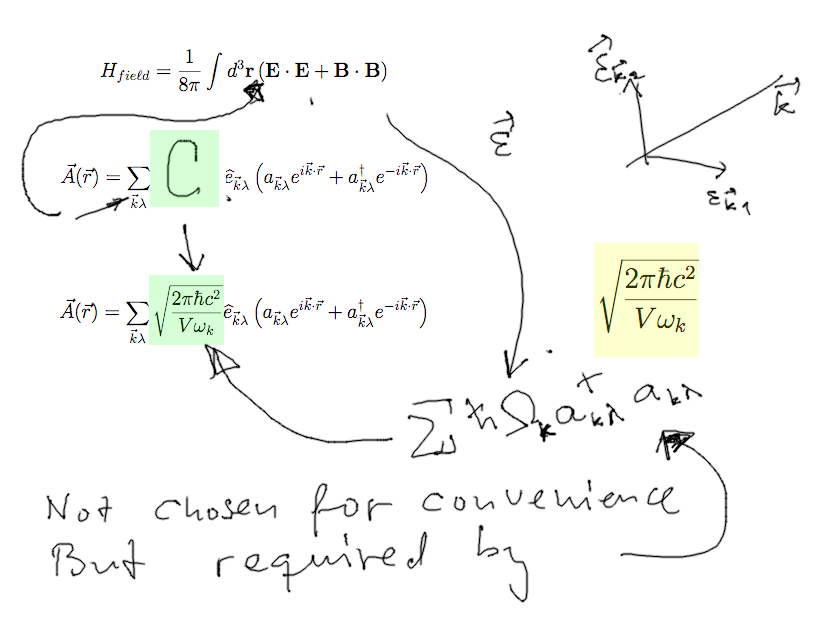 a2-field-energy-QM.png
a2-field-energy-QM.png
 a3-field.png
a3-field.png
Lagrange function and Hamilton function for a charged particle in el mag field
charge-in-elmag-derivation-jpg/ Here are preliminary pictures of pages ....
 a4-doing_particle_in_elmag.png
a4-doing_particle_in_elmag.png
Density of states -
Continuum energies - Quasicontinuum derivations
 b1-density-of-states.png
b1-density-of-states.png
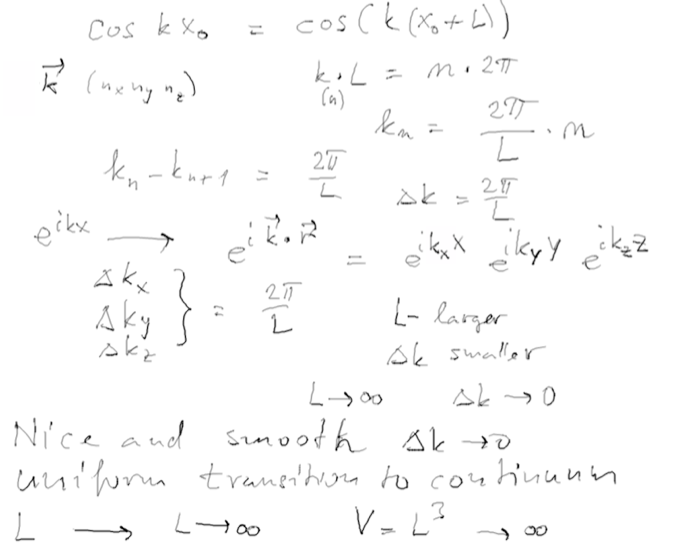 b1-f-density-of-states.png
b1-f-density-of-states.png
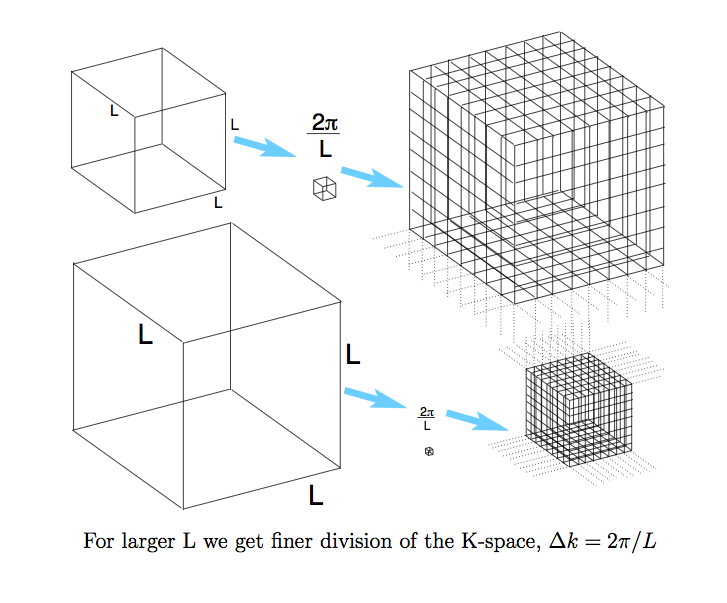 b2-density-of-states.png
b2-density-of-states.png
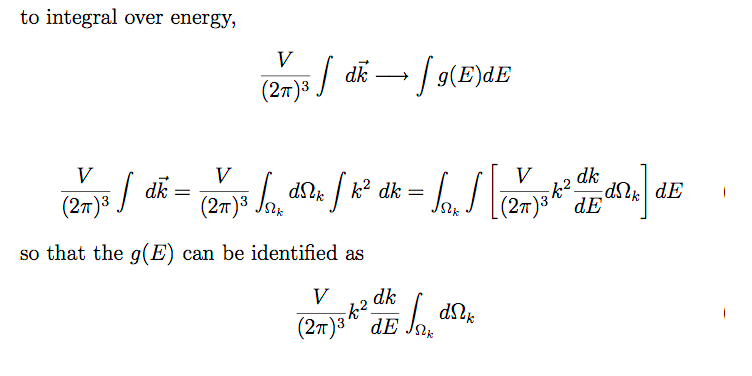 b2-n-factors-density-of-states.png
b2-n-factors-density-of-states.png
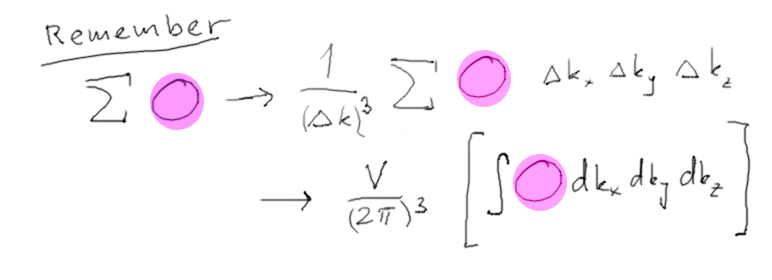
b3-sum_1_over_delta_sum_delta.png (Both picture and
text from PHYS208 Lecture)
The colored "expression" can be anything in the sum (integral) above
The argumet goes like this:
sum -> sum with the
proper deltas which are compensated by the 1/Deltas outside the sum
Then keep the 1/Deltas outside the sum
and concentrate on the Sum with deltas; Taking this
by itself, it will converge to an integral
when you make Deltas infinitesimal
The Deltas outside are not to be made
infinitesimal, SINCE they connect to the original sum
This is sometimes not so easy to keep in mind .... ( the sum
itself would go to infinity ... )
From this follows the dependence of Fermi energy on N/V - the density
(see last time ... )
FINAL
RESULT - Discussion
 ee.png
ee.png
 ff-stimulated_emission.png
ff-stimulated_emission.png
Previous lecture 2010.11.02
to
index
Next lecture 2010.11.16

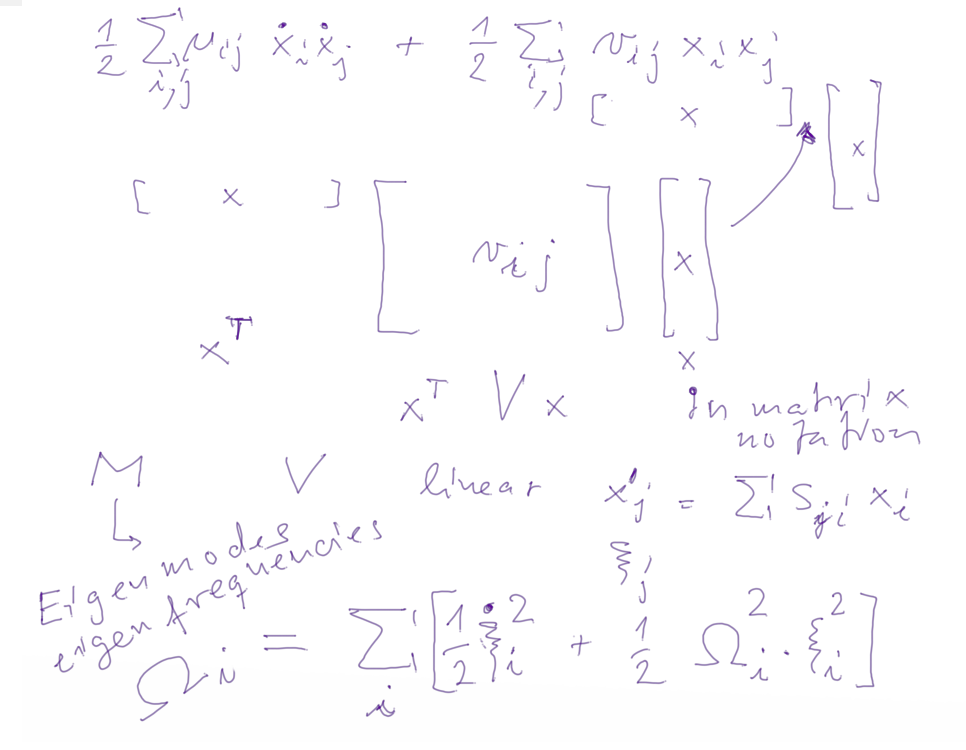
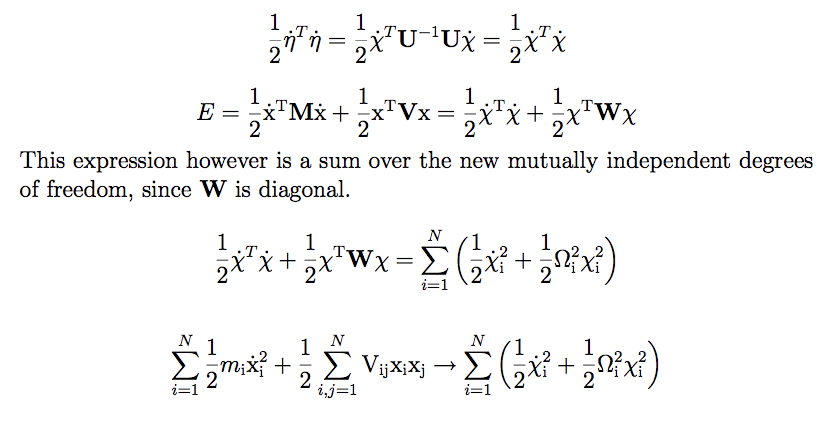 3-eigenmodes-of-coupled-oscillating...png
3-eigenmodes-of-coupled-oscillating...png 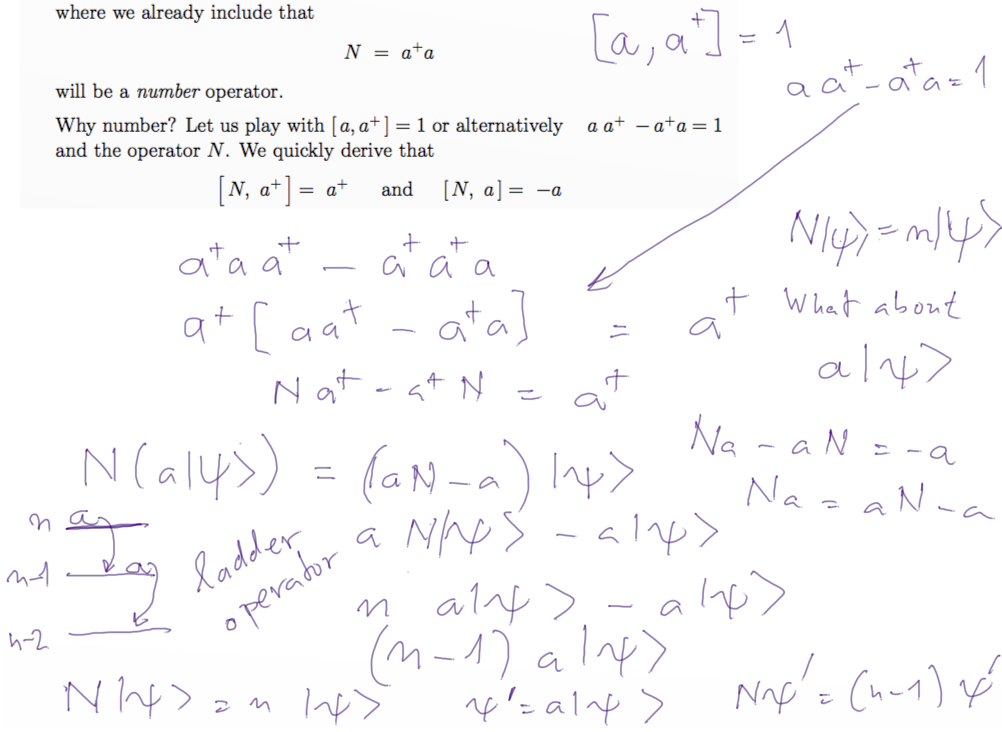 5-QM-harm-oscillator.png
5-QM-harm-oscillator.png  6-extra-QM-harm-oscillator.png
6-extra-QM-harm-oscillator.png  7-Fields.png
7-Fields.png  a1-energy-inmagn-field.png
a1-energy-inmagn-field.png  a2-field-energy-QM.png
a2-field-energy-QM.png  a3-field.png
a3-field.png  a4-doing_particle_in_elmag.png
a4-doing_particle_in_elmag.png  b1-density-of-states.png
b1-density-of-states.png 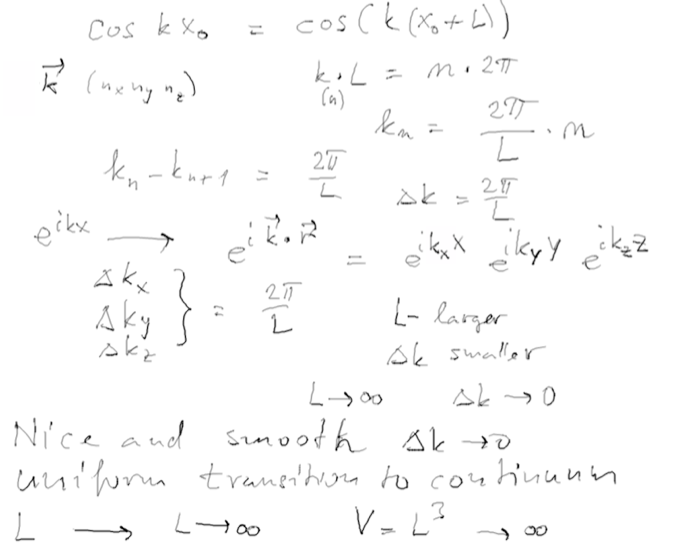 b1-f-density-of-states.png
b1-f-density-of-states.png  b2-density-of-states.png
b2-density-of-states.png 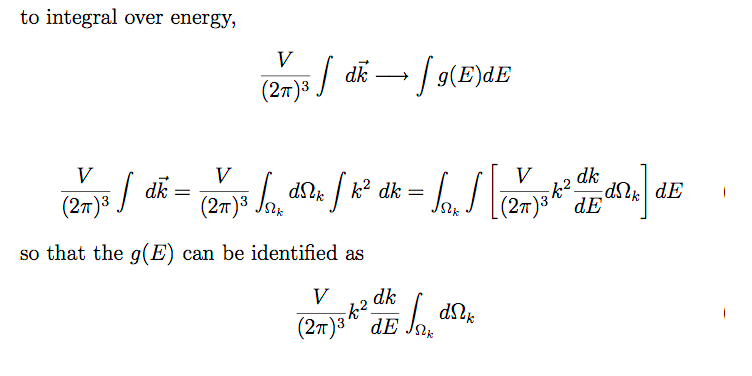 b2-n-factors-density-of-states.png
b2-n-factors-density-of-states.png 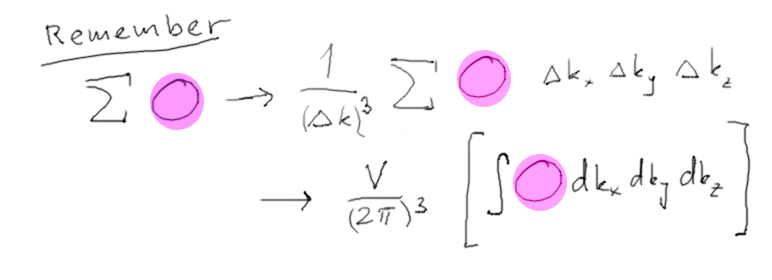
 ee.png
ee.png  ff-stimulated_emission.png
ff-stimulated_emission.png