Huygens Principle. Polarization of electromagnetic waves. Circular polarization
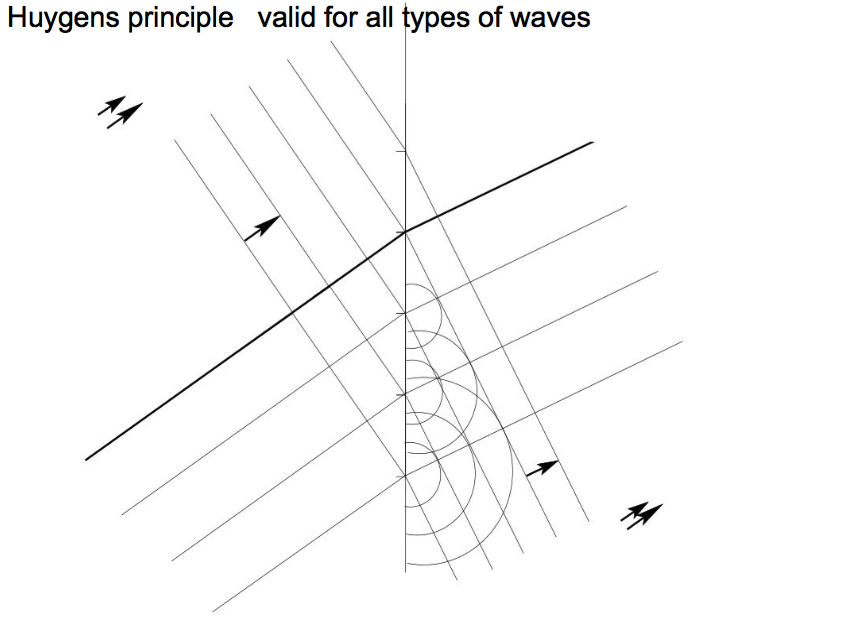
Huygens principle is a simple intuitive picture of wave motion, valid for any type of waves.
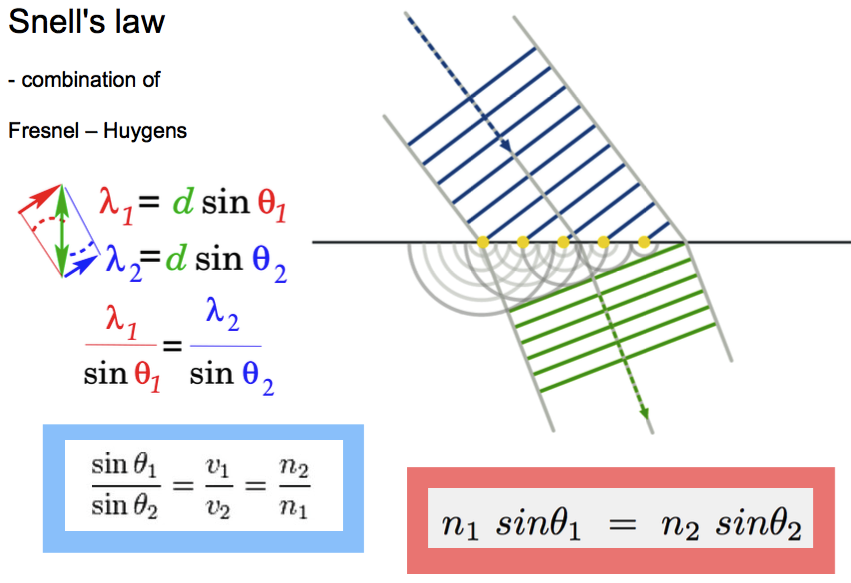
It can be used to understand the so calles Snell's law
Mathematical formulation can be related to the Green's function method

sc_0100.png
Snell's Law for refraction can be simply understood from Huygens principle as shown in the following drawings
What can not be determined is which part of the wave is reflected and which part is refracted to the angle
snell1.png
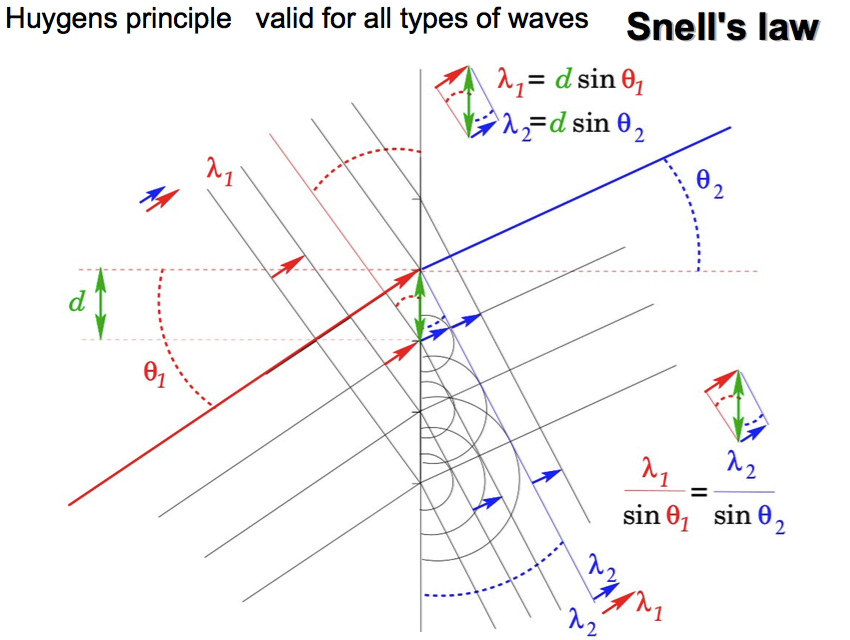
The following drawing shows that Snell's law is connected with the two wavelengths - rather than the speeds of propagations
If the wavelength is shorter in medium 2, the propagation angle (measured from the normal) is smaller
snell2.png
For all waves where the phase velocity is independent of wavelength: the frequency = velocity divided by wavelength
Since the frequency must remain unchanged in the two media, shorter wavelength in medium 2 means lower velocity
Therefore, if the picture of refraction is as indicated, the velocity in medium 2 is smaller
Thus index of refraction (inversely proportional to the spead) is larger for medium 2
snell3.png
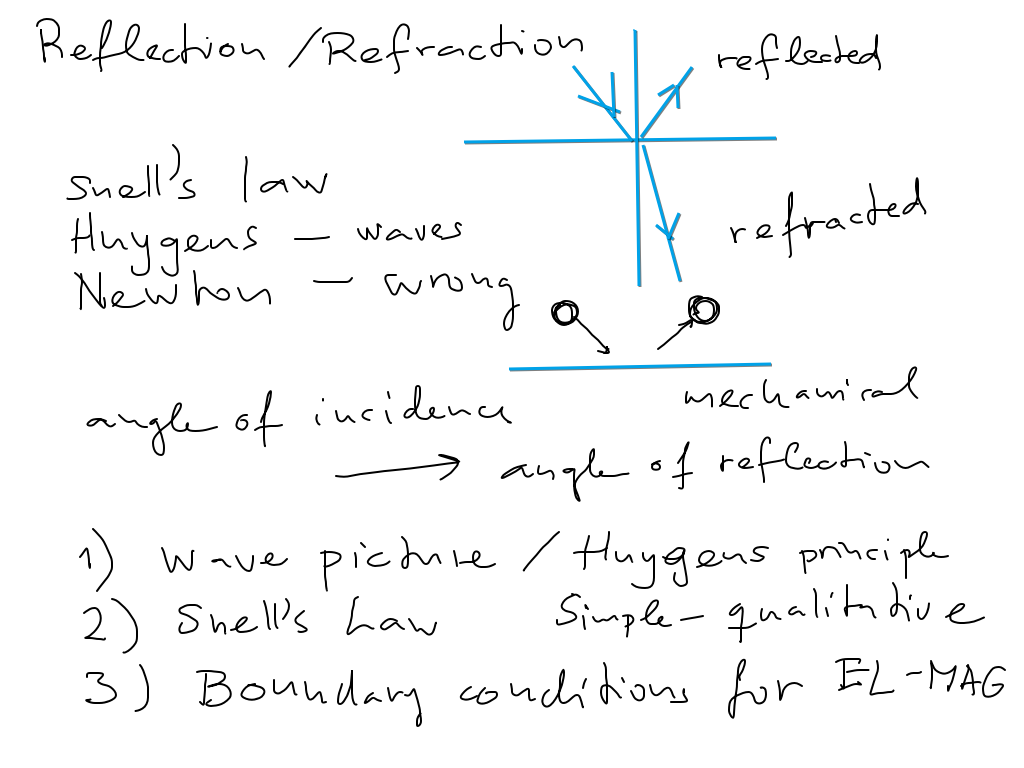
If light consisted of particles, Snell's law would be satisfied if particles would get a push forward, i.e. move
with a larger velocity in medium 2. This was believed by Newton
sc_0200.png
To determine how the electromagnetic wave behaves at the interface, we must add the "boundary conditions"
to the analysis.
The relations are shown in the following drawing
The parallel component of E and the normal component of B are continuous
From Gauss law, the normal component of E is changed according to the relation below.
For most materials, B remains constant (permeability changes are roughly negligible)
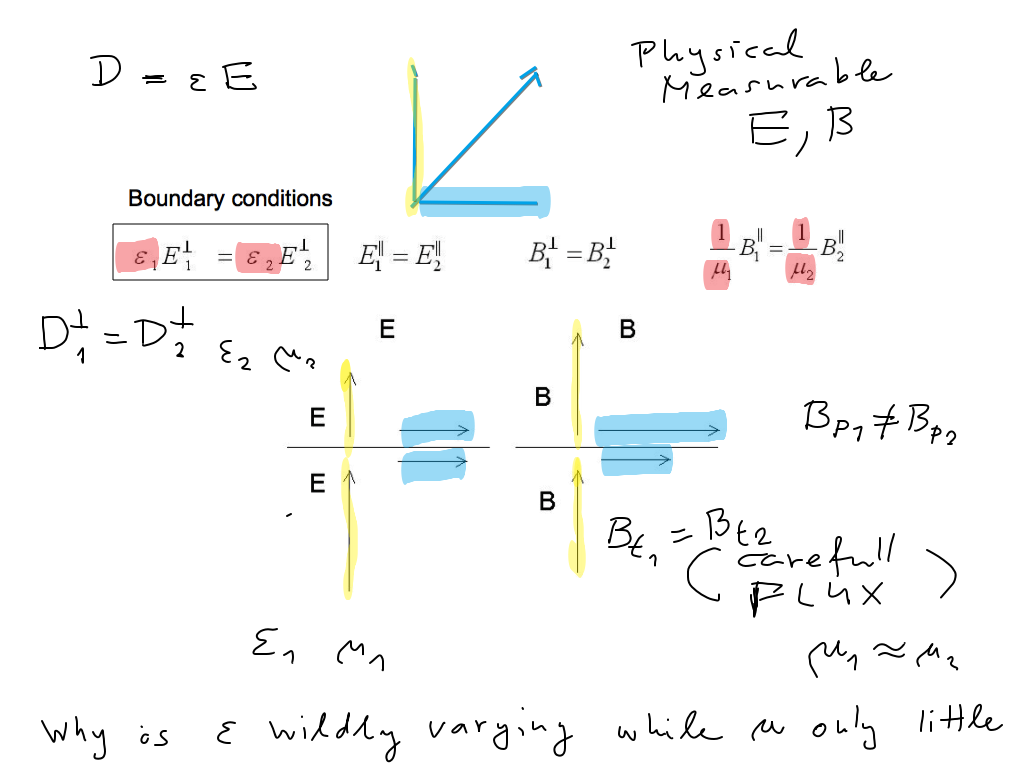
sc_0300.png
Thus the behaviour of the wave at the interface will be determined by the relations above.
Electromagnetic waves are transverse waves. The wave can be polarized in any direction (perpendicular to propagation)
Waves can be superposed - and decomposed
It is thus enough to consider behaviour of waves with polarization(s) which allow simple analysis
That means two simple waves - with E in the pane of incidence, and with E perpendicular to that plane
This we shall explore next time
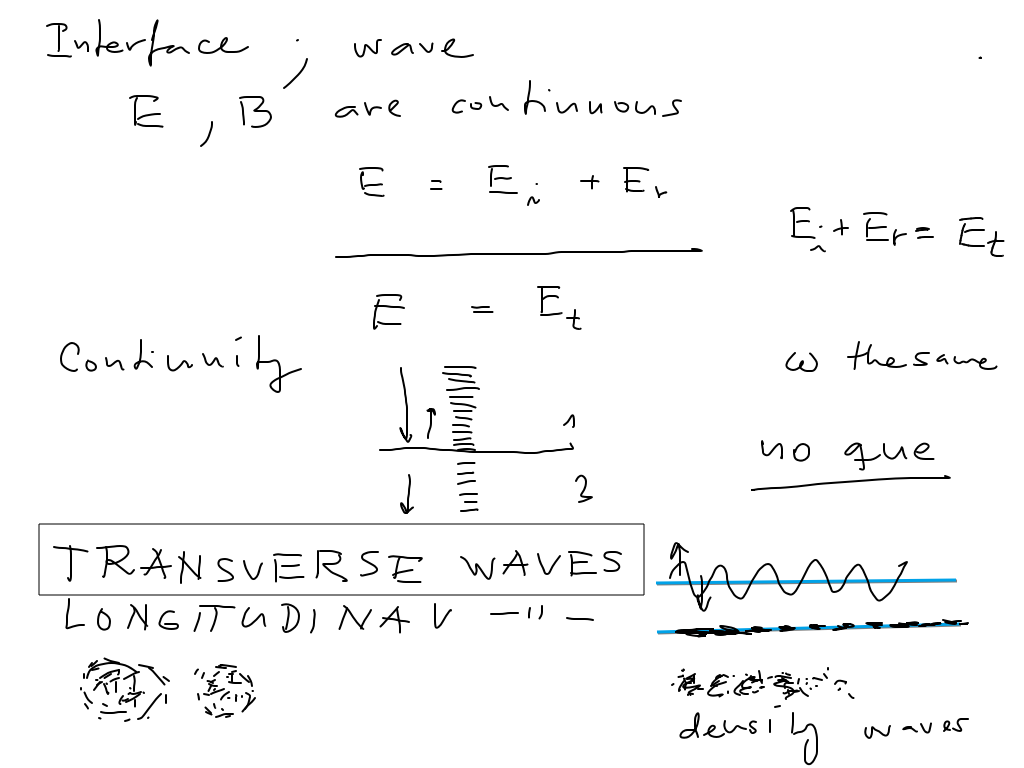
sc_0400.png
More on polarization - intuitive pictures
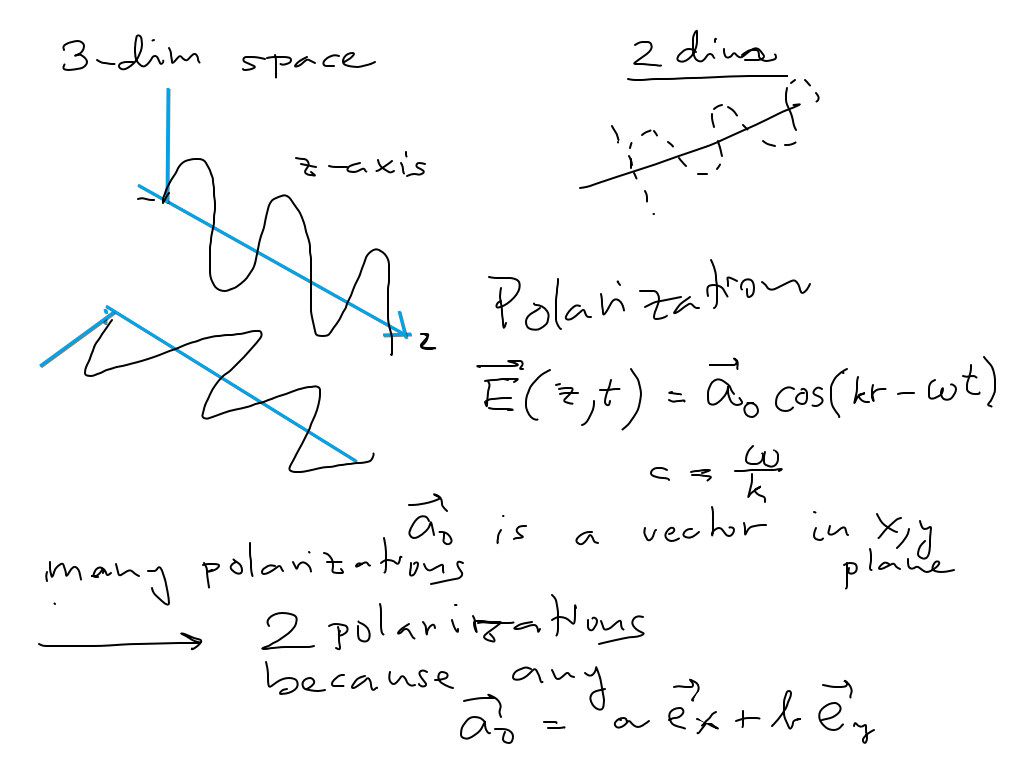
sc_0500.png
But in addition to the discussed "linear polarization" which can be decomposed into two perpendicular components
There is also a possibility to have CIRCULAR polarization
(and elliptic - meaning that the two phase delayed perpendicular
motions have different amplitudes )
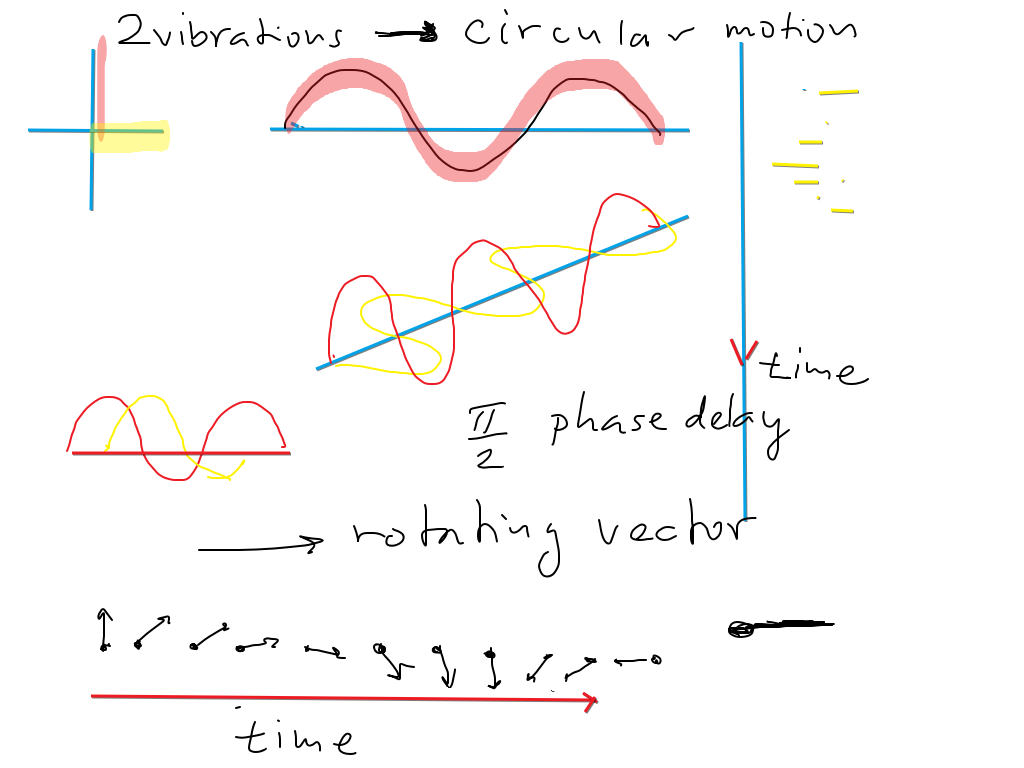
sc_0600.png
Circular polarization and complex notation
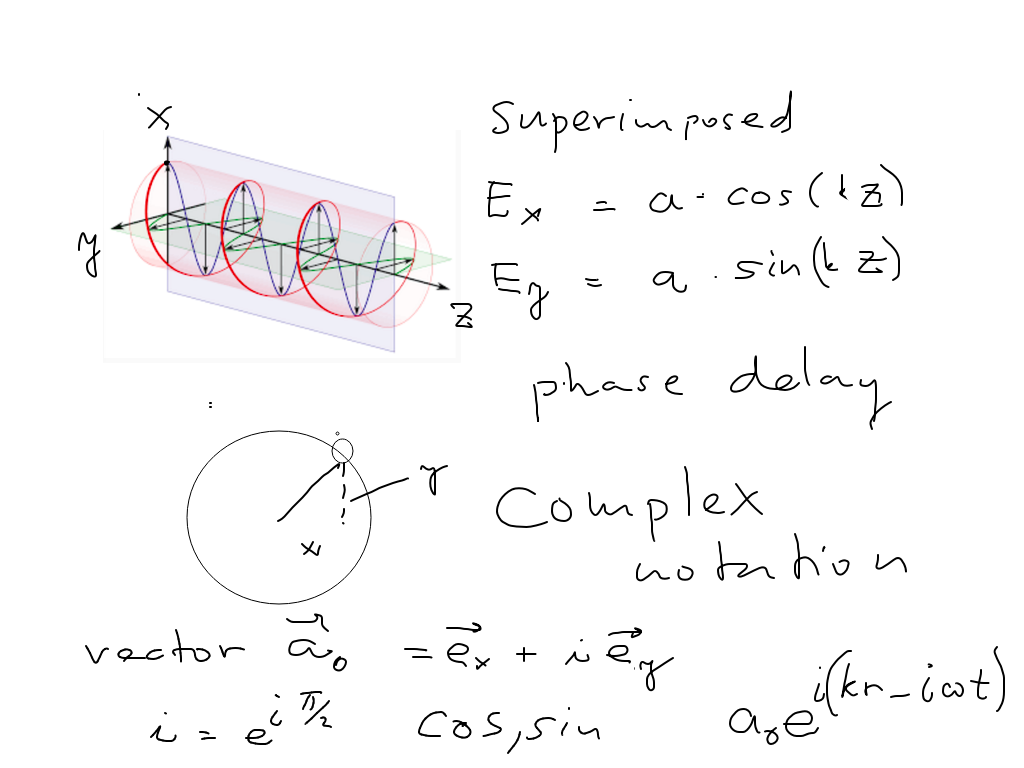
sc_0700.png
Next time: More formal relations on polarization;
Notation - P-wave and S-wave also TE-polarized and TM-polarized
Details of S-wave and P-wave reflection/refraction