Some additional comments
Creation and annihilation - the ladder operators - and the LADDER - the equidistant spectrum of the oscillator

sc_0300.png
The integration over directions - the density of states - a large version of the picture
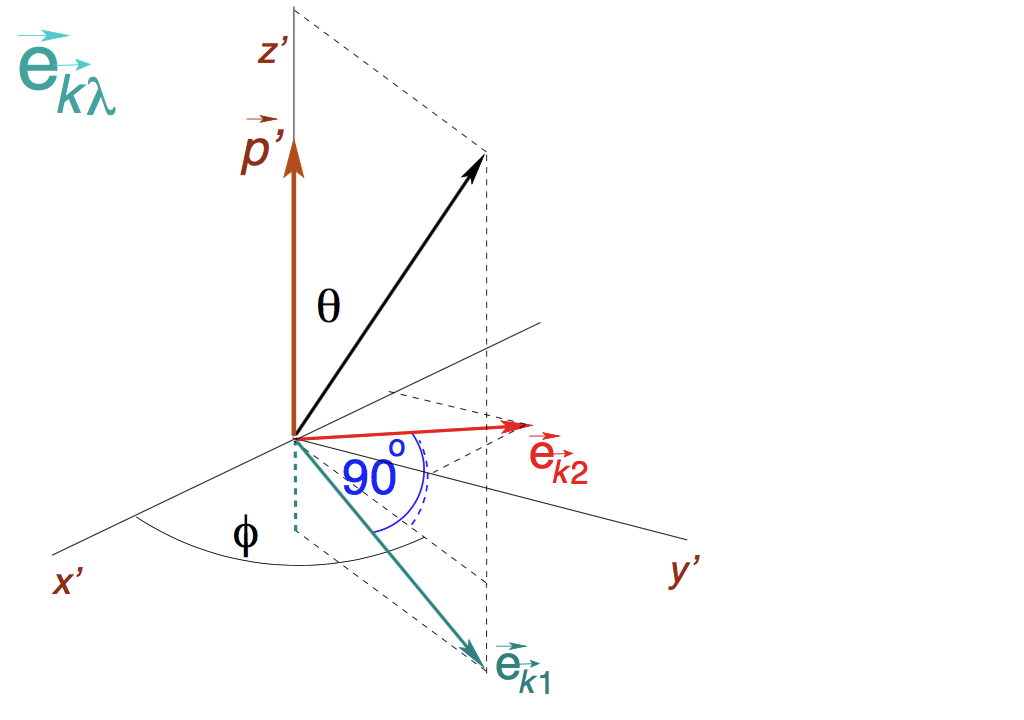
sc_0600.png
Back to the "two expansions" - and the simulation of the Golden rule - with stress on the NATURAL LINE WIDTH
The "width" appears in the eigenstates of the "total hamiltonian"
Here is the lecture sketch togethe with later added snapshots from the presentation
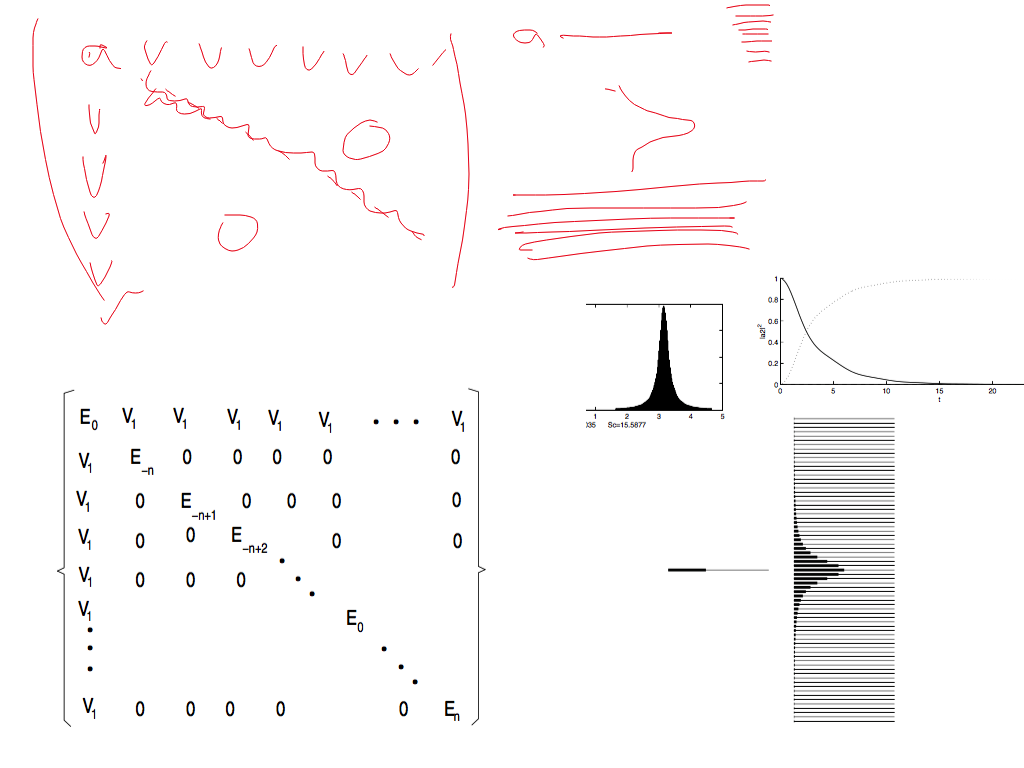
sc_0700.png
Playing with matlab - the matrix, the diagonalization
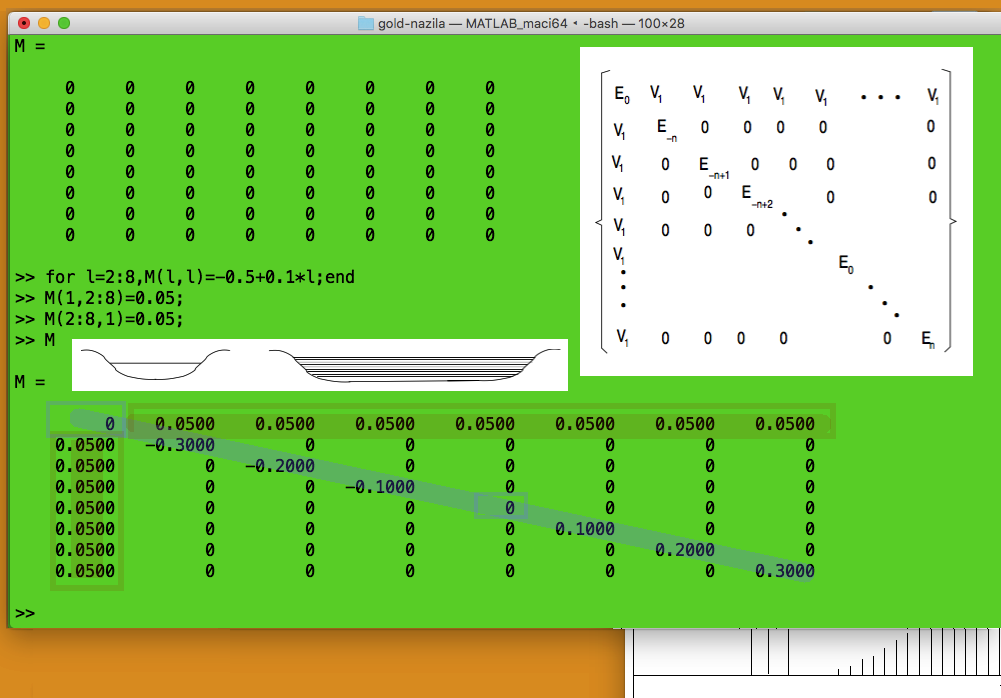
sc_0750.png
The eigenvectors and eigenvalues
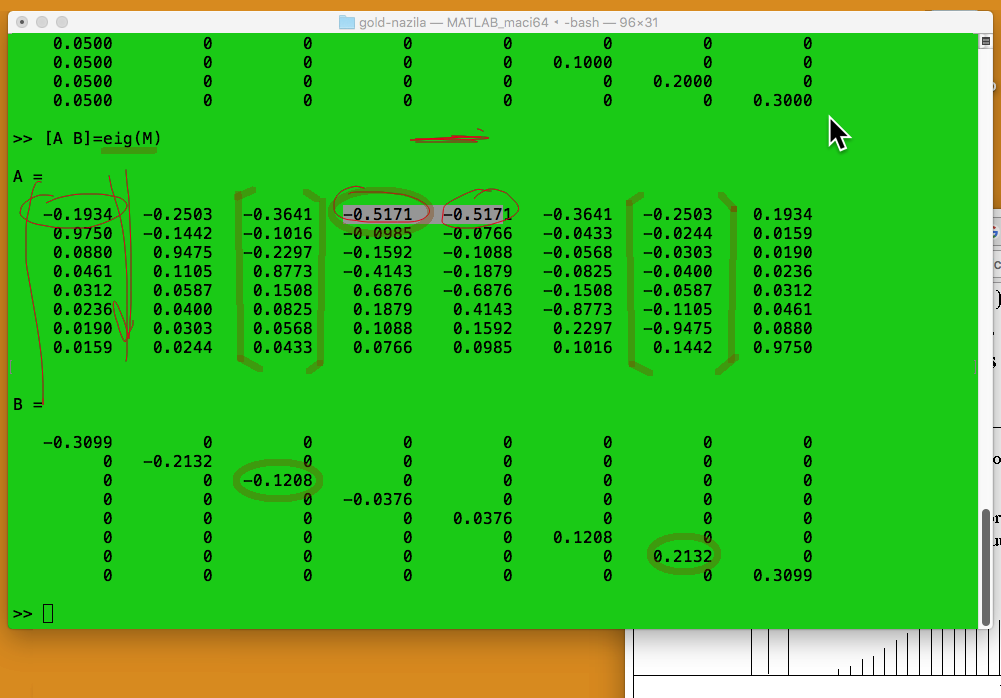
sc_0800.png
The eigenvectors squared - the probability amplitudes - the natural width illustrated
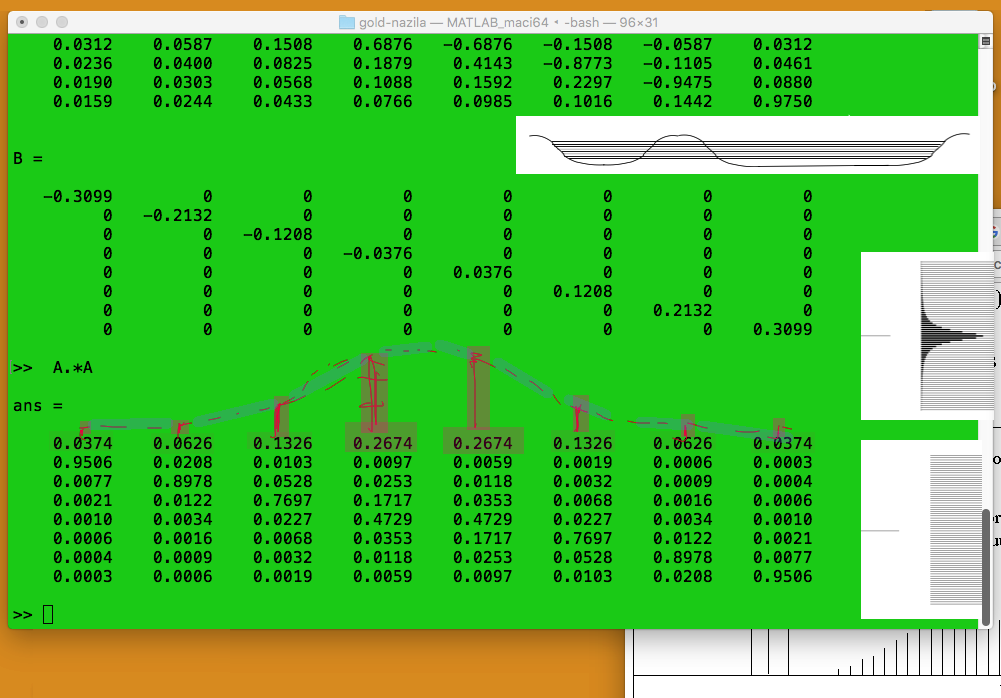
sc_0900.png
Older matlab version of the Golden rule program - the matlab diagonalization above - the dots
On this picture the state has decayed ....
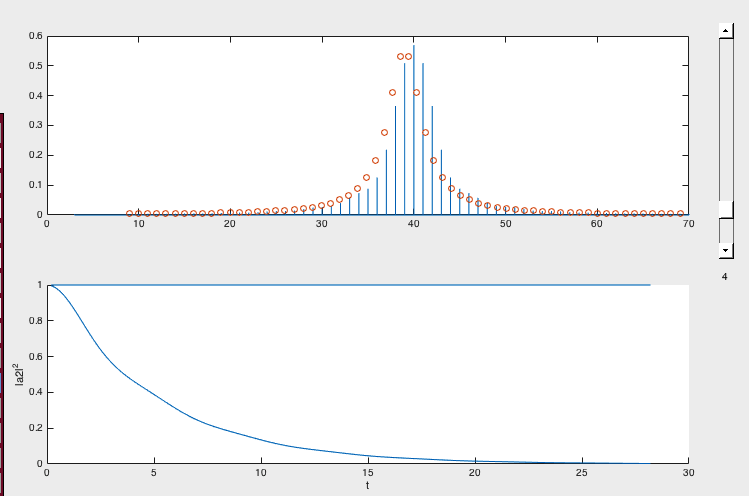
zZP1_large_time.png
Older matlab version of the Golden rule program - the matlab diagonalization above - the dots
On this picture the state has NOT YET decayed ....
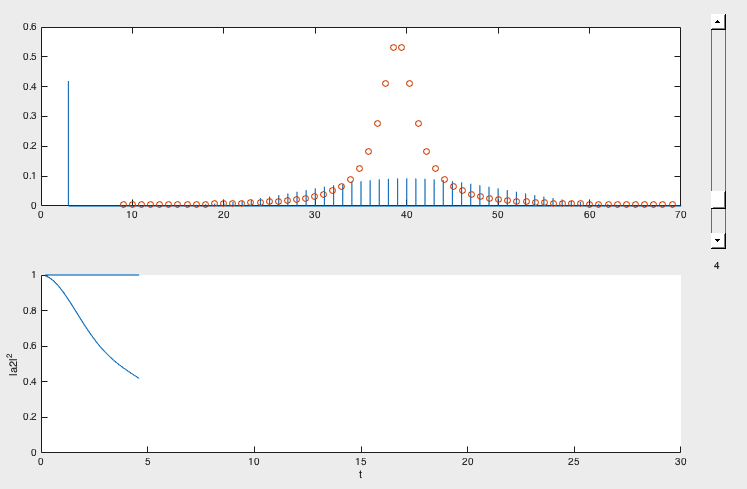
zZP2_small_time.png
Here we look at 12 states only - in the pictures and below in the numerical part of the program
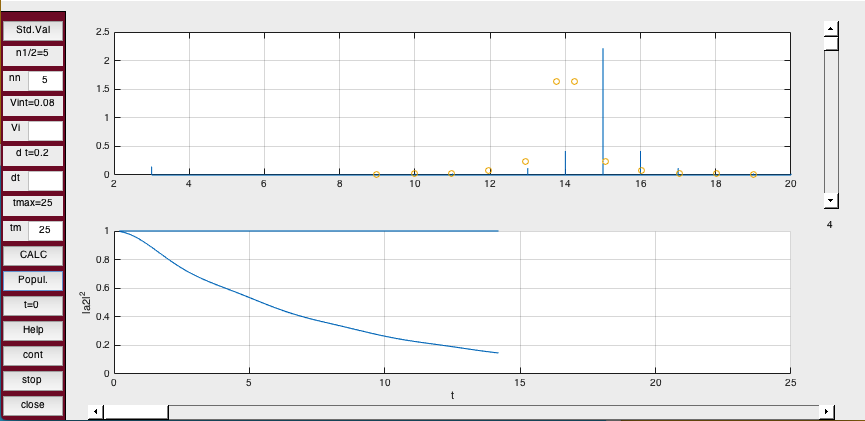
zZP3_small_N.png
Here we look at 12 states only - in the numerical part of the program - the picture above is running
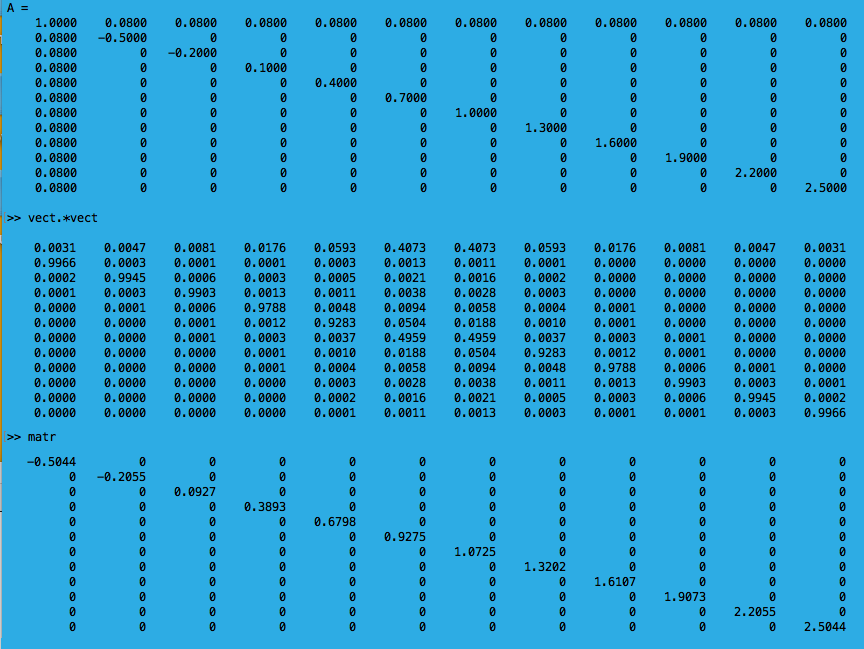
zZP4-term_small_N.png
Here is one calculation - with long time scale the state has decayed .....
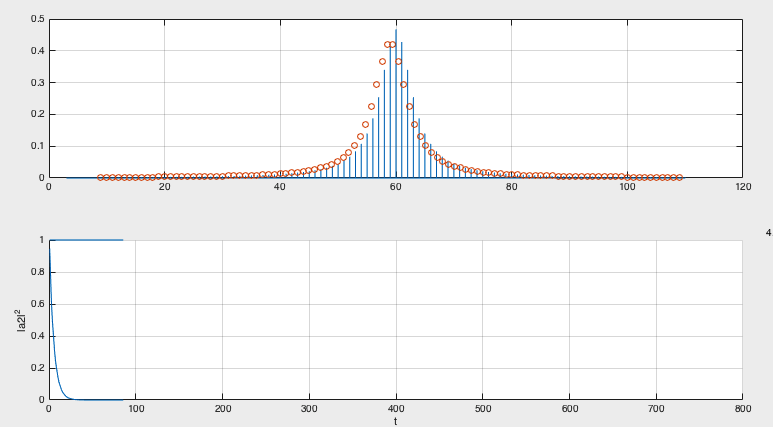
zZP5_decayed.png
But for large times we see so called recurrences - the original state comes back
The "quasiperiod" of the recurrences can be found to depend on the energy (frequency) spacing
For truly continuous case - delta omega -> 0 i.e. T -> infinity
Recurrencies happen in real cavity experiments - when the eigenmode spectrum is similar to this model
Sometimes this is called Collapse and Revival
See e.g. https://en.wikipedia.org/wiki/Quantum_revival
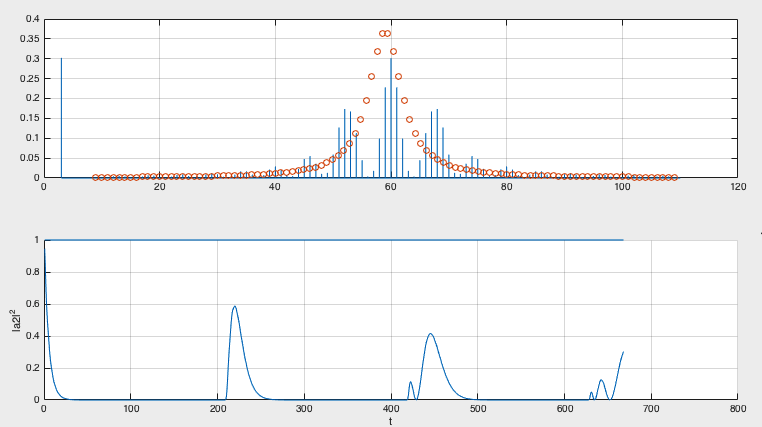
zZP6_decayed_Reccurence.png
Next: various additional aspects