2010.09.21 previous lecture
note
2010.09.28 next lecture note
HELIUM -PART 3
 0-He-coordinates.png
0-He-coordinates.png
The spectrum of helium. For the first column - the singlet and
triplet parts are separated.
To the right is the case when one electron is free.
The original picture is in the EXAM SLIDES
Doubly excited states - the electrons would be bound, but because of
their repulsion
the total energy is high so that one electron can be ejected.
Thus we get autoionizing states
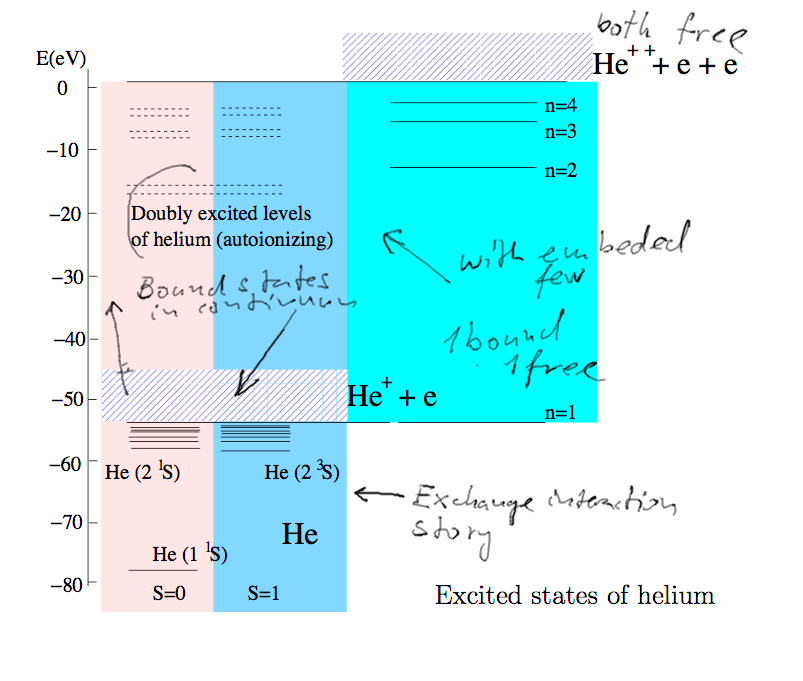 a-1-excited-helium.png
a-1-excited-helium.png
Part of the table - just for helium. This is about the role of
the 'perturbation term' 5/8
Z E0
 a-2-Perturbation-He-table.png
a-2-Perturbation-He-table.png
The whole
table, with only perturbation part
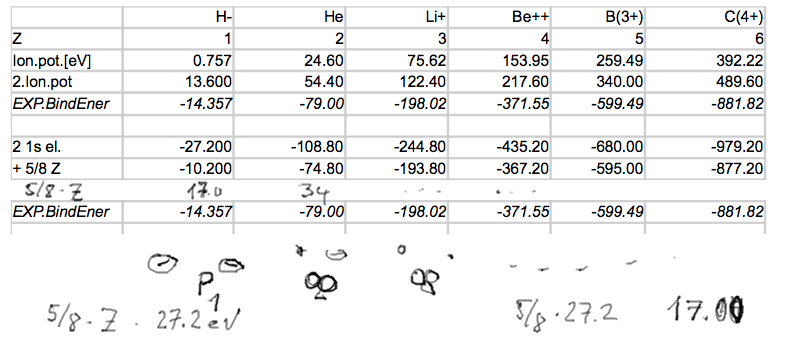 a-3-Perturbation-table.png
a-3-Perturbation-table.png
Evaluation of
the repulsion - the multipole expansion
 b1-repulsion.png
b1-repulsion.png
Spherical harmonics integral - for
ground state we only need one term - all three zeros
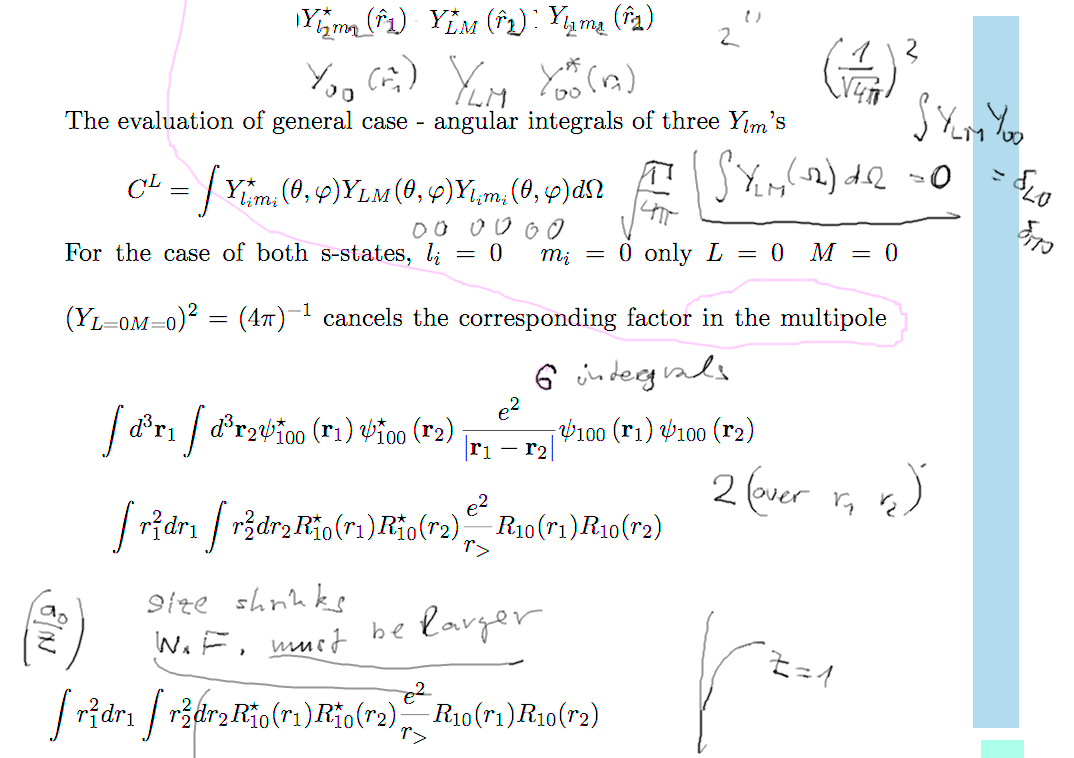 b2-repulsion.png
b2-repulsion.png
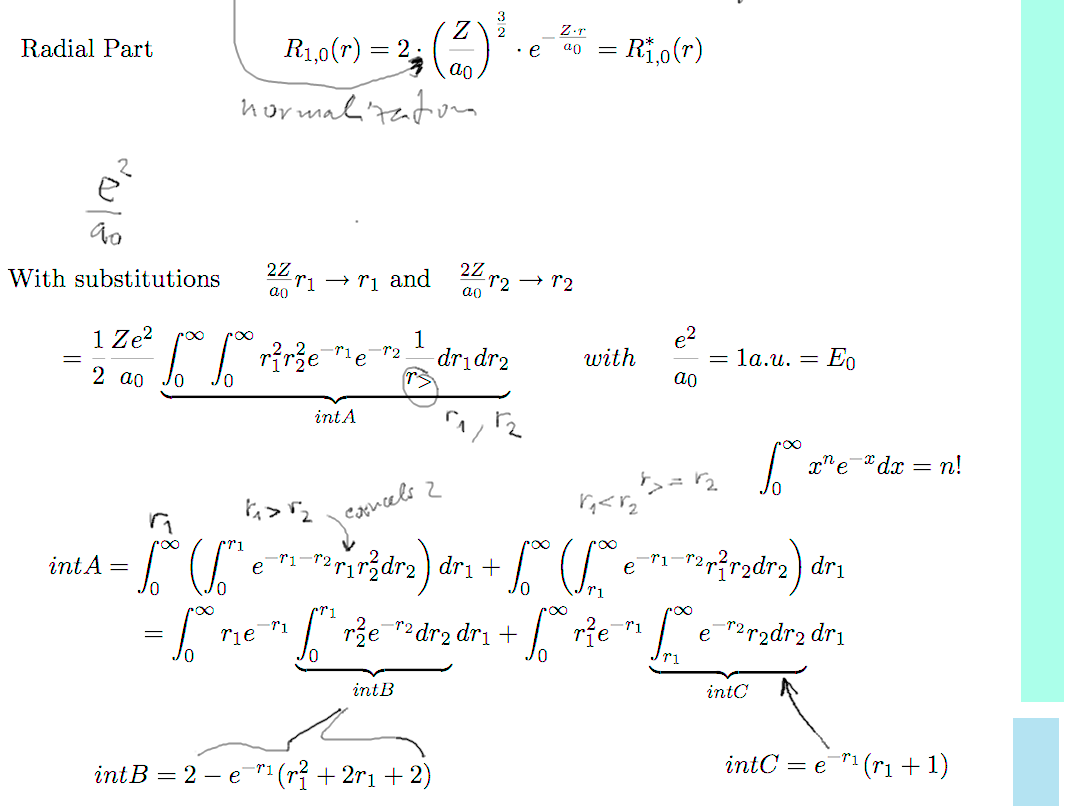 b3-repulsion.png
b3-repulsion.png
 b4-repulsion.png
b4-repulsion.png
Done - perturbation theory for the ground state. How is it for
the excited states, when antisymmetric functions
must be used
 d-1-perturbation-excited-state.png
d-1-perturbation-excited-state.png
This is originally from the many-electron atoms EXAM SLIDES
excited states, when antisymmetric functions must be
used
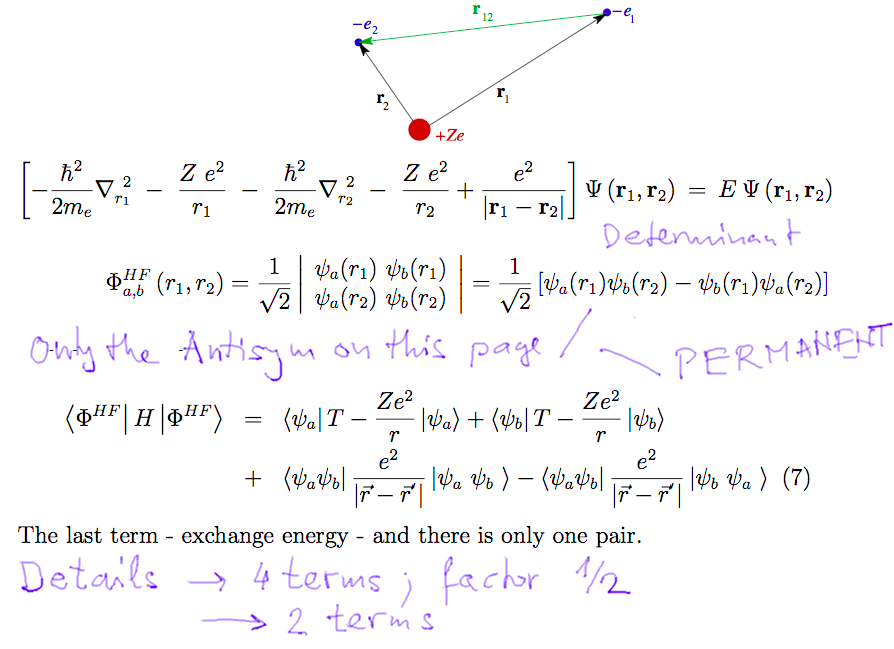 d-15-excited-state-evaluate.png
d-15-excited-state-evaluate.png
VARIATIONAL METHOD FOR GROUND STATE
OF HELIUM
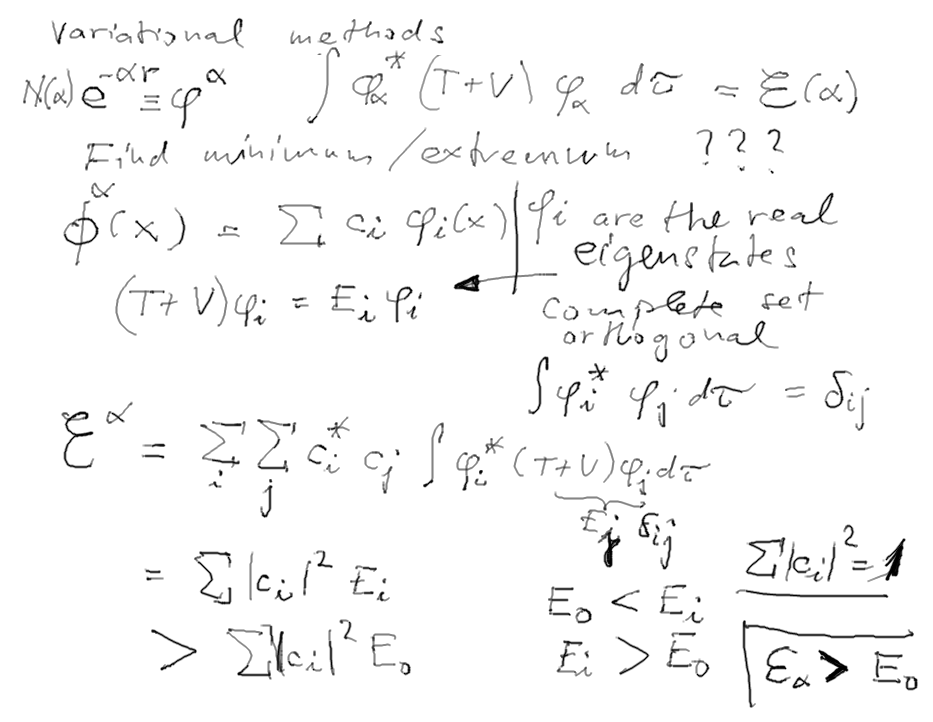 d-2-variational-1.png
d-2-variational-1.png
 d-3-variational-2.png
d-3-variational-2.png
LATER WE SHALL USE A SLIGHTLY more free theory - without assumed
normalization.
That is important to get "variational principle for Schrödinger
equation" - this all later
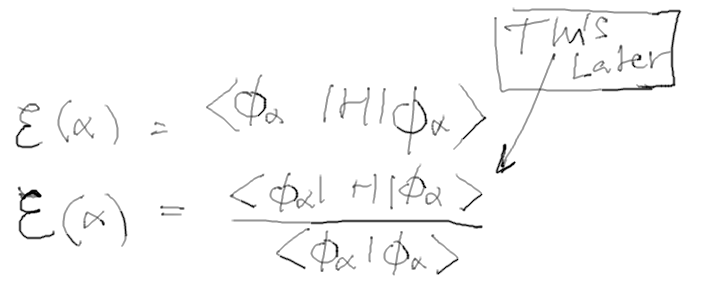 d-4-variational-2.png
d-4-variational-2.png
Details of the variational
calculation
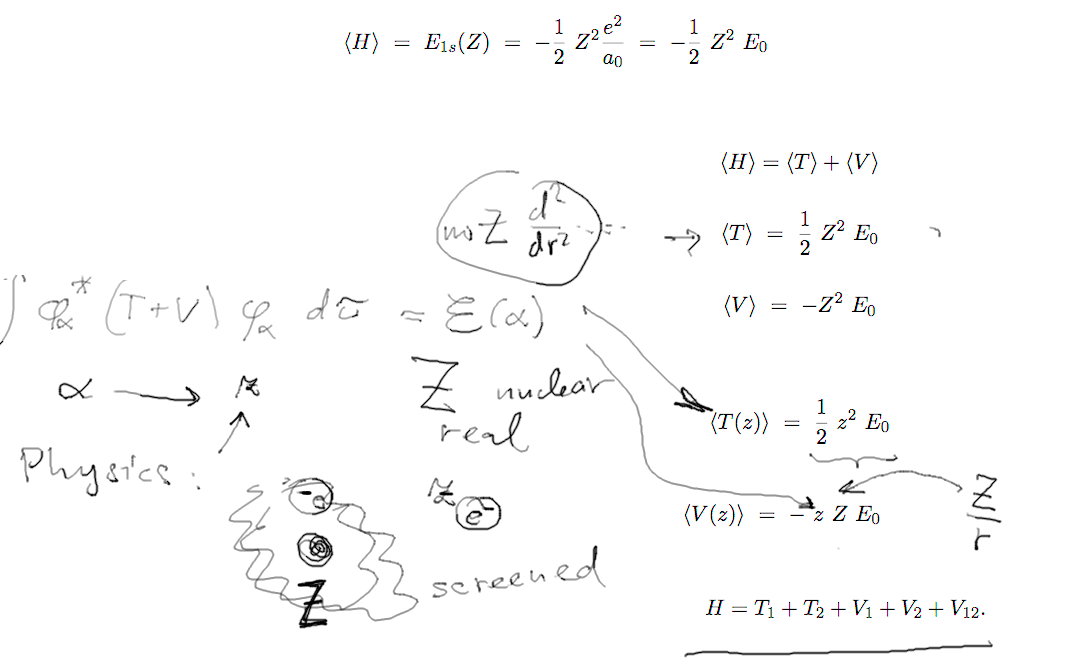 d-4-variational.png
d-4-variational.png
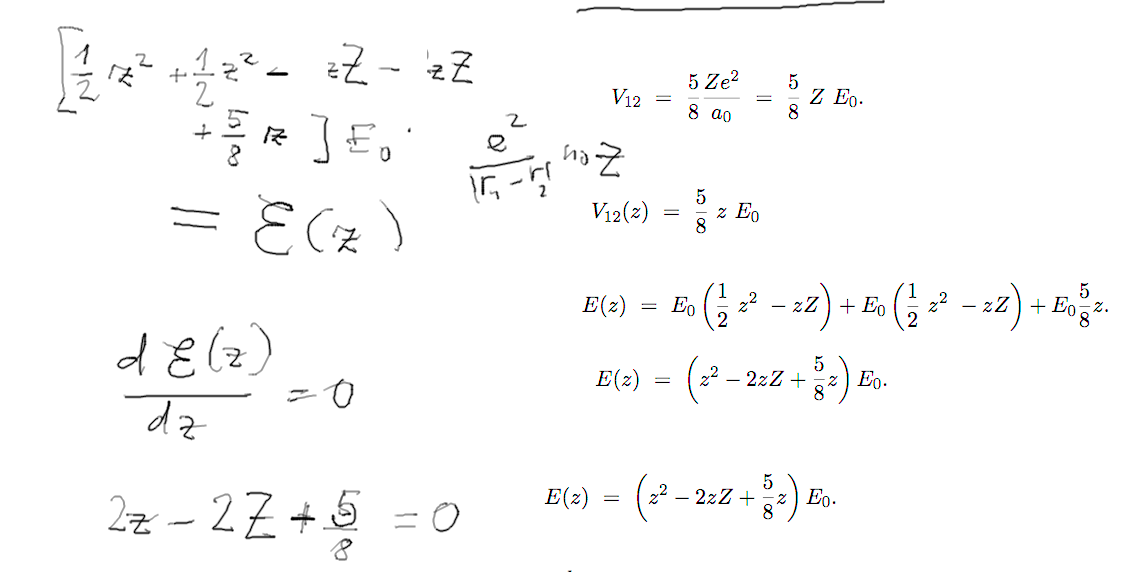 d-6-variational.png
d-6-variational.png
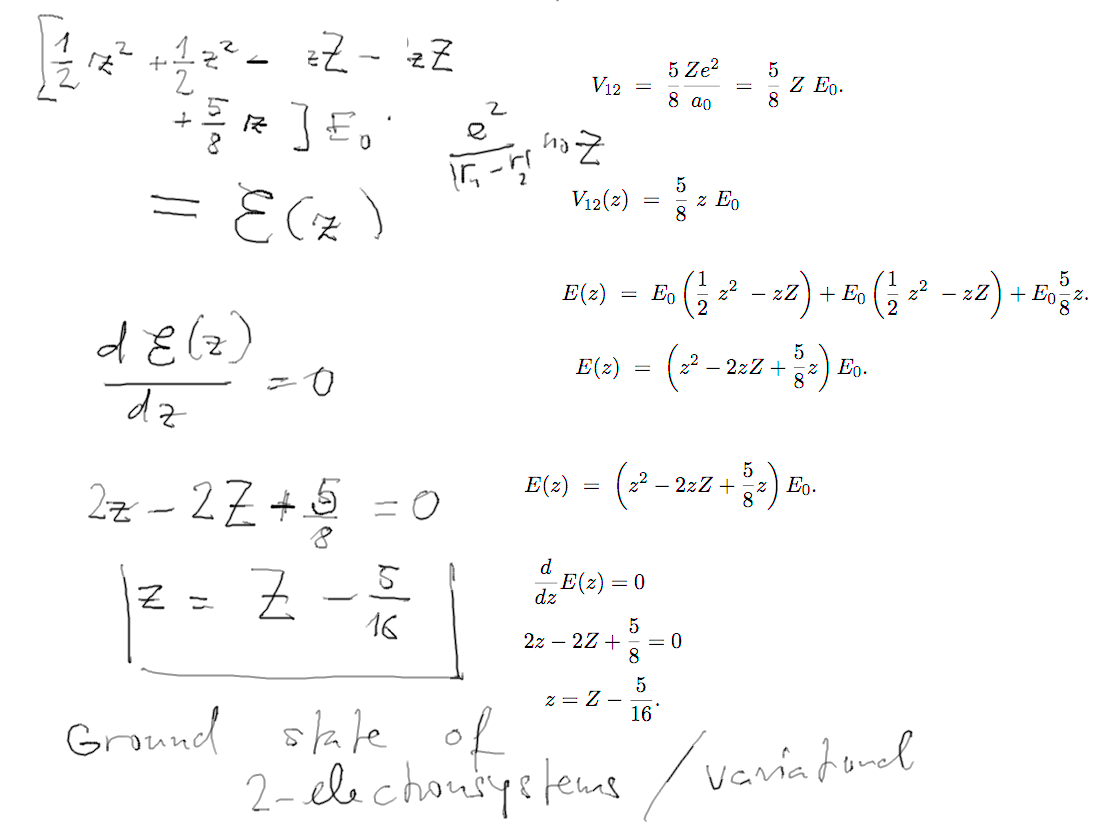 d-7-variational.png
d-7-variational.png
The final results are summarized in the table which is in the EXAM
SLIDES.
It can also be obtained from the spreadsheet (we have both xls
(microsoft) - and ods (the world-
OpenOffice) formats (advice: use ODS,
OpenOffice)
You can also see the HTML version for quick
information (without the calculations).
SUMMARY OF HELIUM
 q4.png
q4.png
 q5.png
q5.png
The case of disappearing excited state.
A circle can not have first excited state - it has an infinite
excitation energy
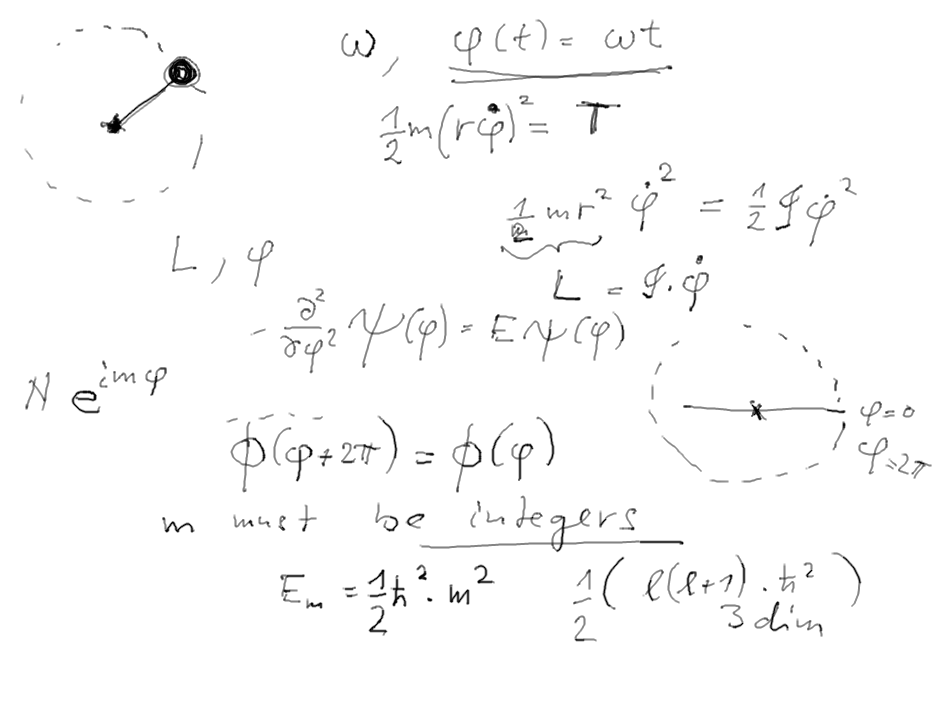 q6.png
q6.png
As the rotator gets 2 identical ends, three, four and then general
N corners (balls),
the region of variable phi shrinks from 2pi to pi (N=2), 2pi/3
(N=3) etc.
Consequently, the first excited state gets HIGHER and HIGHER
 q7.png
q7.png
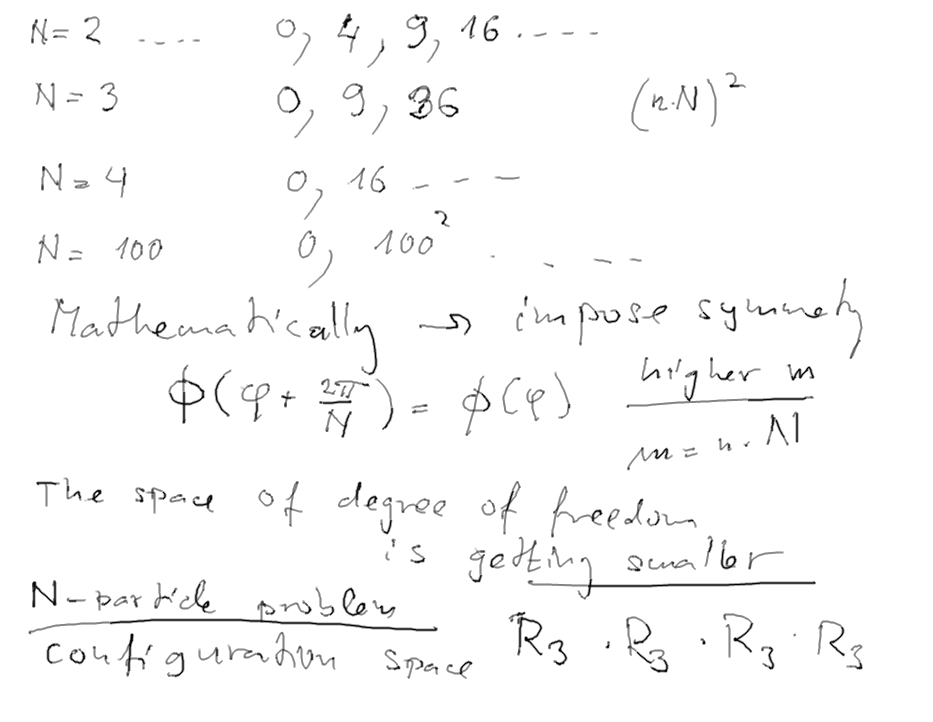 q8.png
q8.png
This is an illustration of what the "identical" and "symmetry" can
mean: it means eliminating the regions of variable(s)
which are not physical (i.e. not a part of the consistent model)
NEXT:
MANY ELECTRON ATOMS
2010.09.21 previous lecture
note
2010.09.28 next lecture note
 0-He-coordinates.png
0-He-coordinates.png  a-1-excited-helium.png
a-1-excited-helium.png  a-2-Perturbation-He-table.png
a-2-Perturbation-He-table.png
 a-3-Perturbation-table.png
a-3-Perturbation-table.png  b1-repulsion.png
b1-repulsion.png 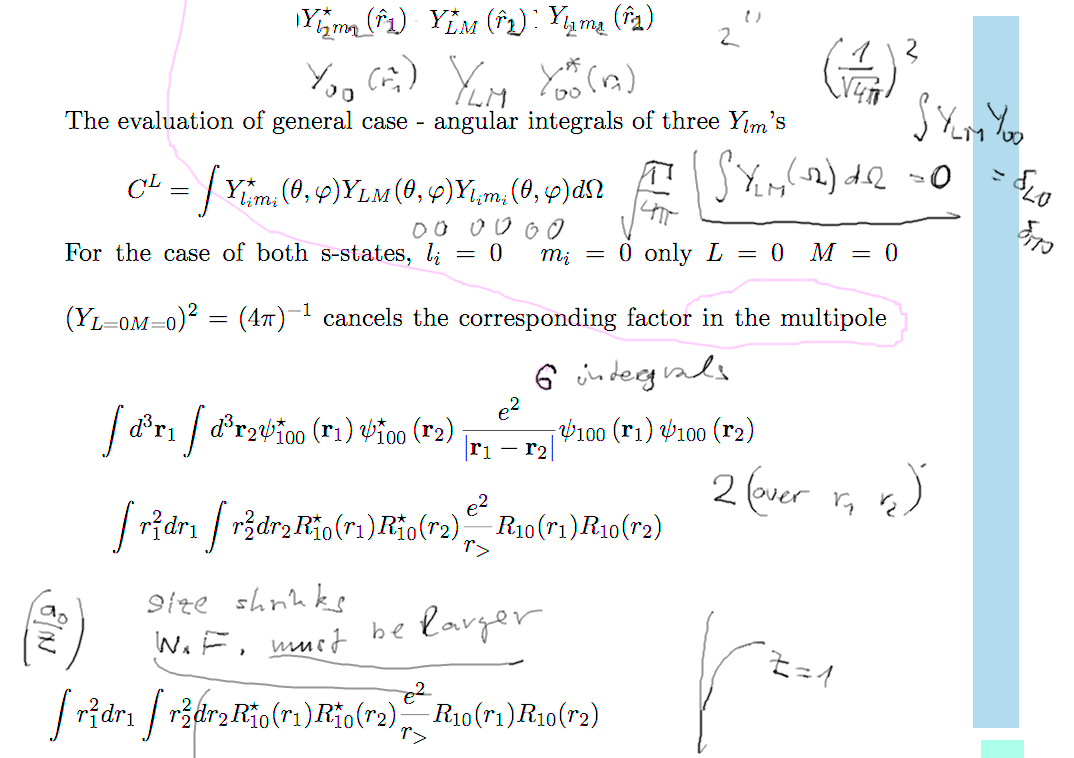 b2-repulsion.png
b2-repulsion.png 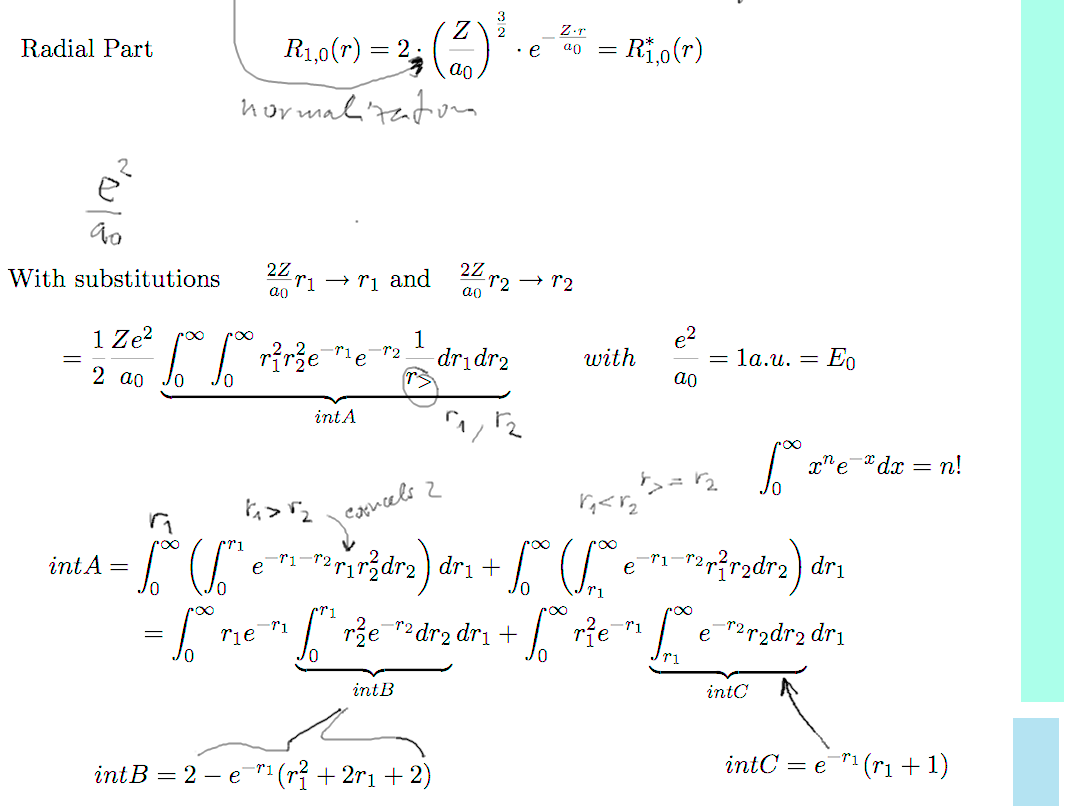 b3-repulsion.png
b3-repulsion.png  b4-repulsion.png
b4-repulsion.png  d-1-perturbation-excited-state.png
d-1-perturbation-excited-state.png  d-15-excited-state-evaluate.png
d-15-excited-state-evaluate.png
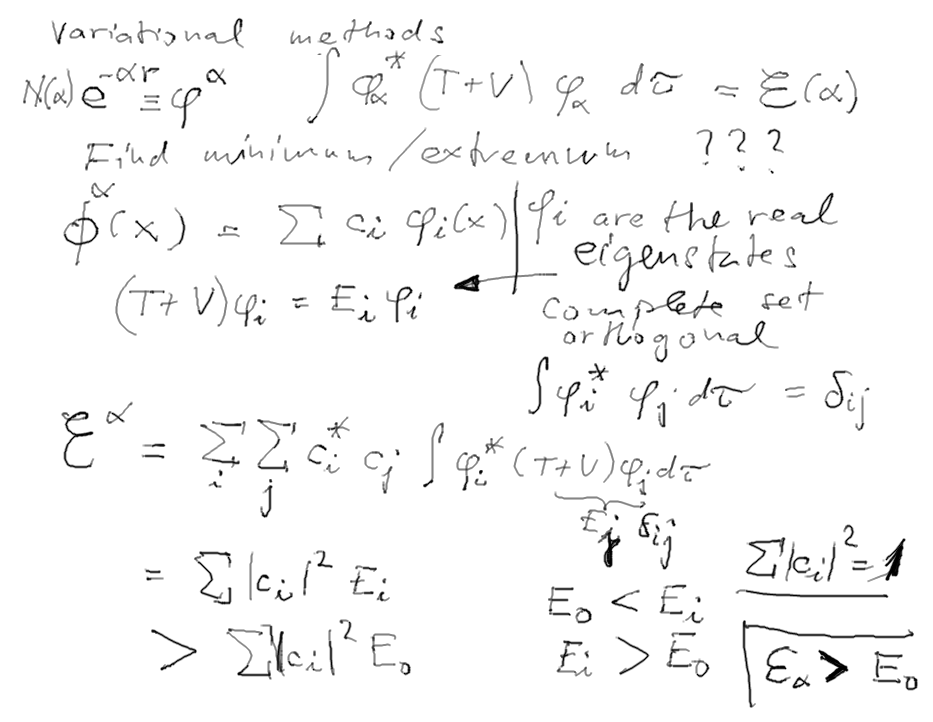 d-2-variational-1.png
d-2-variational-1.png  d-3-variational-2.png
d-3-variational-2.png  d-4-variational-2.png
d-4-variational-2.png  d-4-variational.png
d-4-variational.png 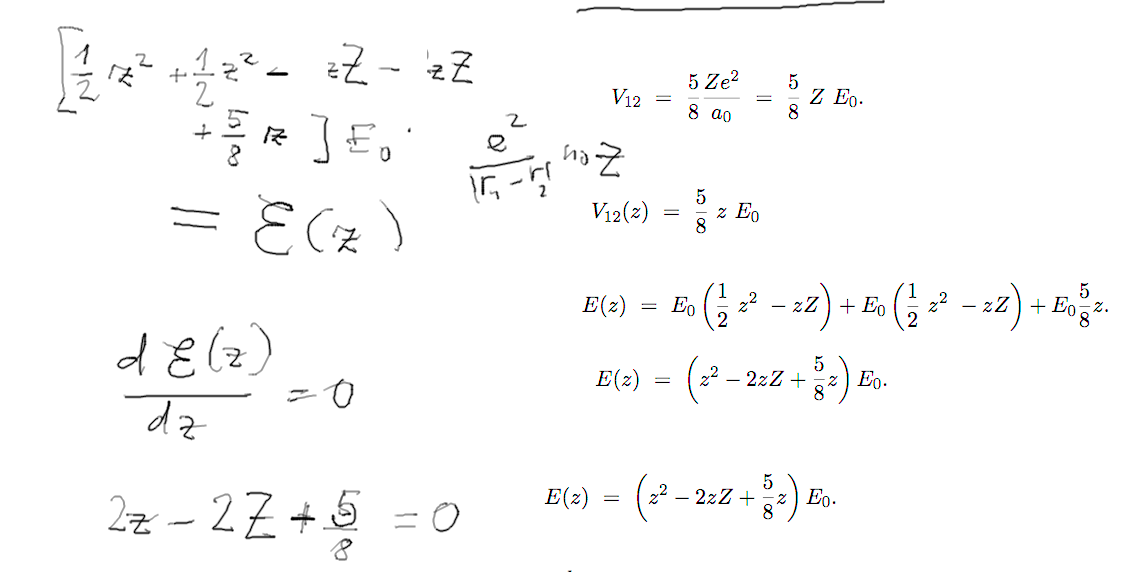 d-6-variational.png
d-6-variational.png 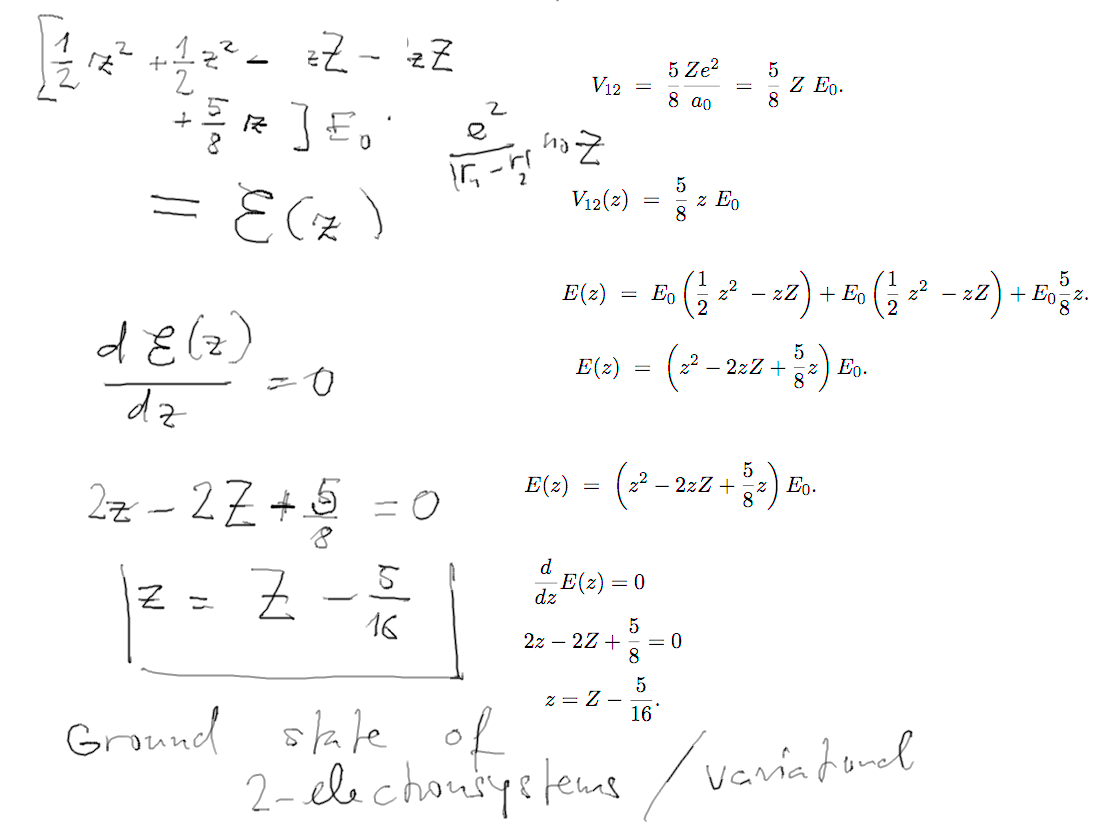 d-7-variational.png
d-7-variational.png  q4.png
q4.png  q5.png
q5.png 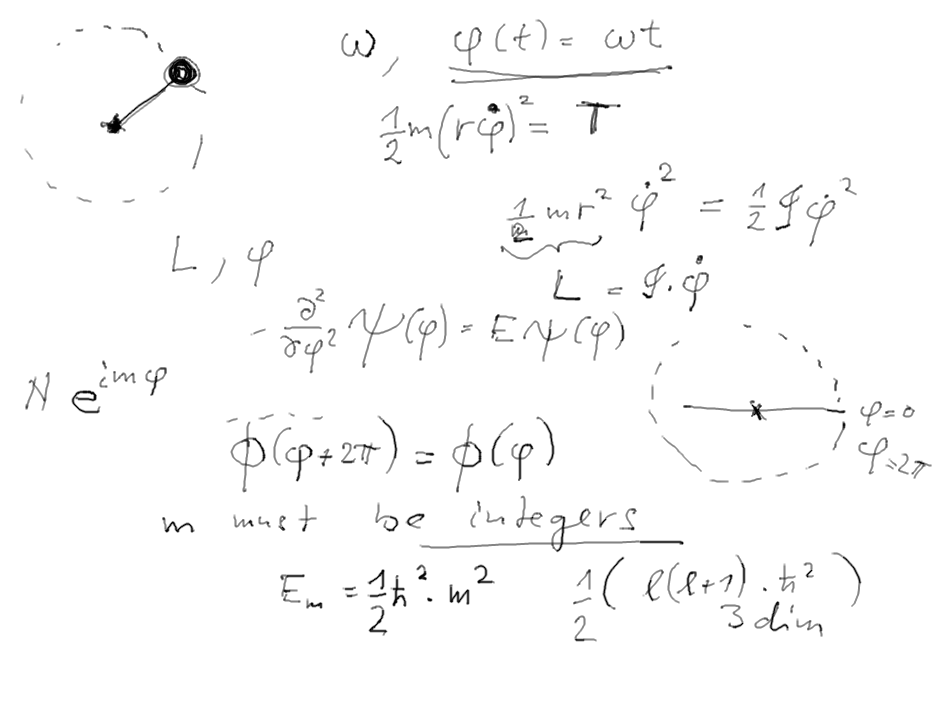 q6.png
q6.png  q7.png
q7.png
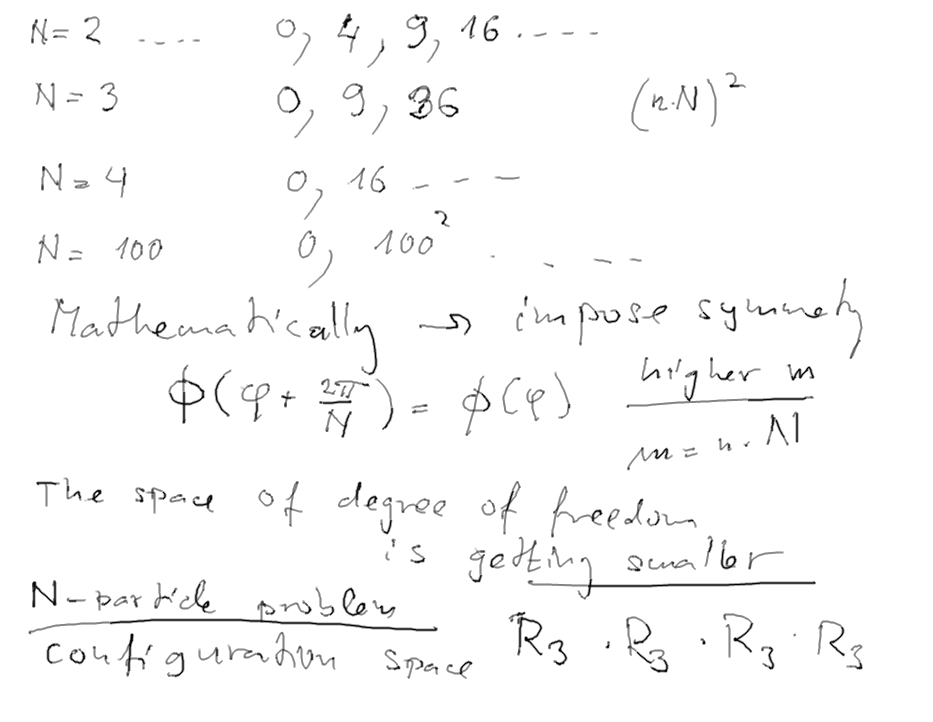 q8.png
q8.png