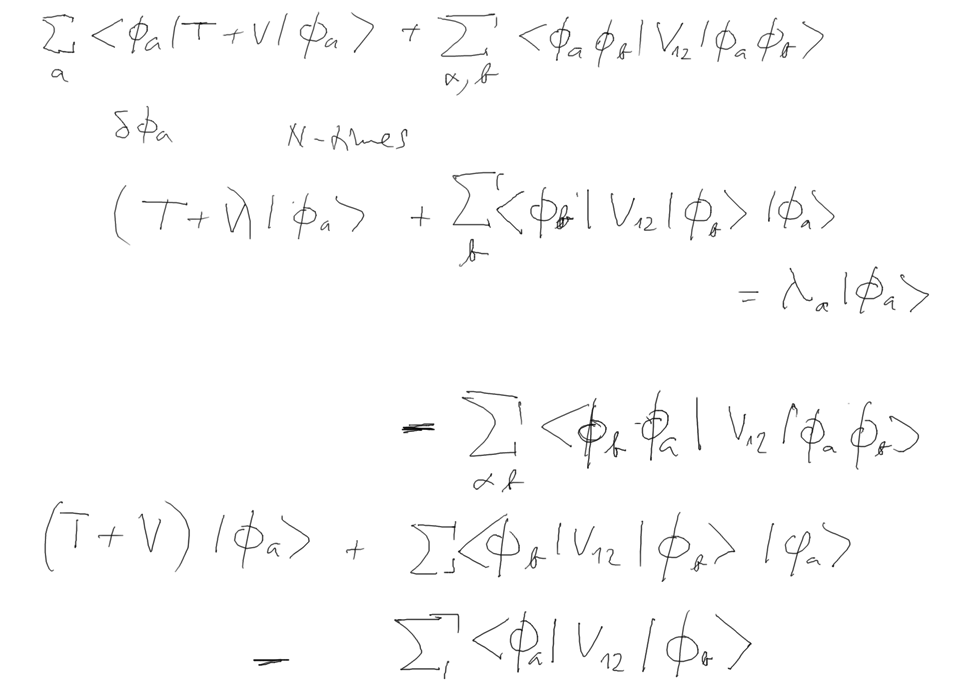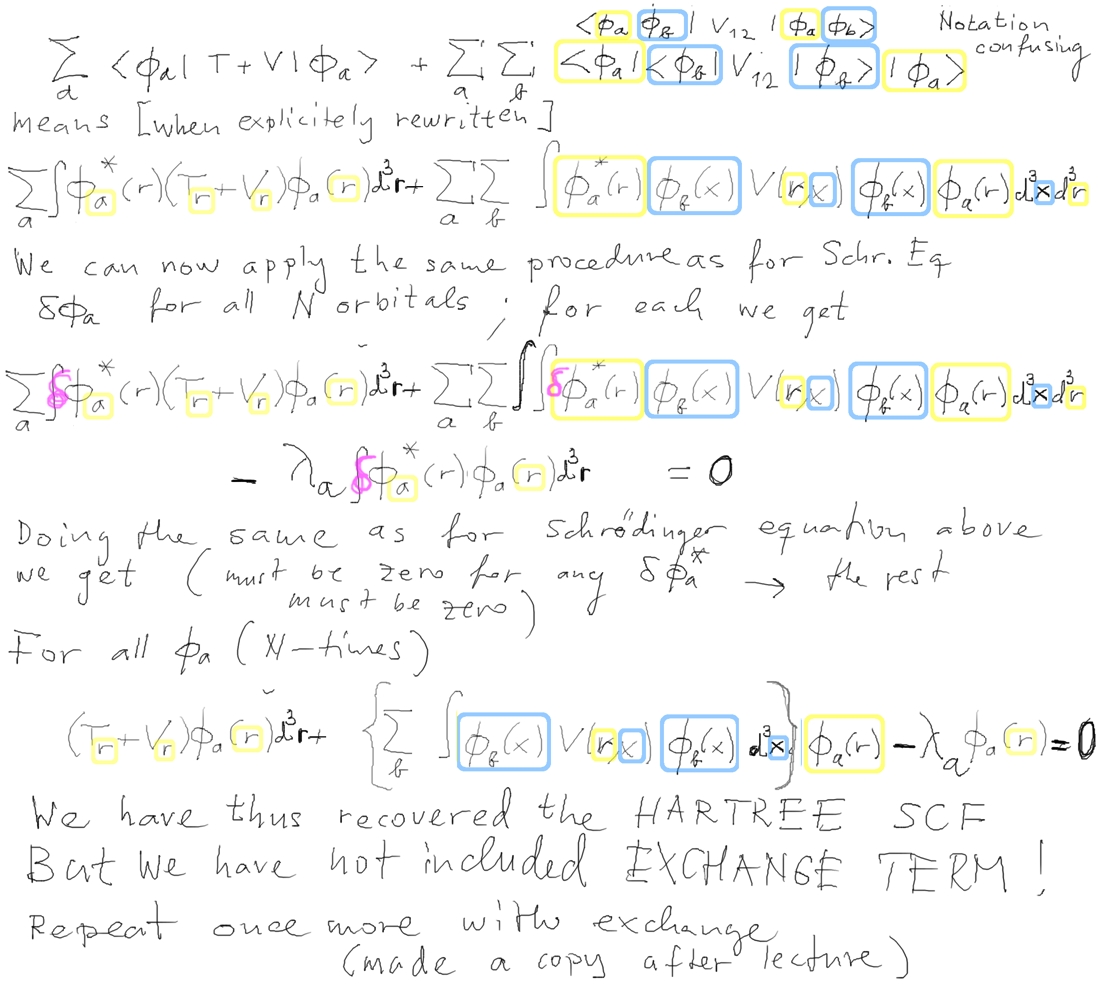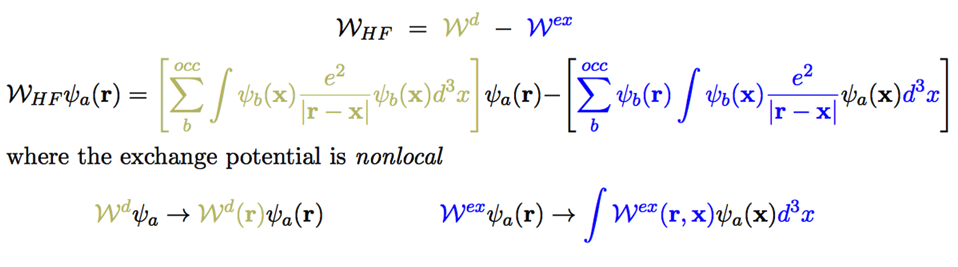Comment: First part of the lecture -
presentation of the
Physical Optics part.
2
presentations discussed
Plan:
Pair interaction result in more detail
Schrödinger equation from variational method
Variational method -
deriving Hartree-Fock Equations
Hartree-Fock Equations
Total energy and the selfconsistent
orbital energies (not finished)
Hartree and Hartree-Fock - Variational
derivation
Detail derivation - counting the nonzero terms (Pair
interaction result in more detail)
1-how-many-nonzero-terms.png

1-how-many-nonzero-terms.png
Sum
over
pairs of coordinates is transformed into a sum over pairs of
orbitals
2-pairs-coordinates-TO-pairs-orbitals.png

2-pairs-coordinates-TO-pairs-orbitals.png
Schrödinger Equation
from variational approach - how to do that
3-Schroedinger_from_variation.png

3-Schroedinger_from_variation.png
Schrödinger Equation
from variational approach - include the normalization
as an extra condition - minimum with a constraint - Lagrange Multiplier
4-conditional_minimum_variation.png

4-conditional_minimum_variation.png
( above is an attempt to illustrate how the minimum is moving until it
is placed on yhe "condition curve" )
5-Schroedinger_from_variation.png

5-Schroedinger_from_variation.png
This is the first attempt to derive Hartree (neglecting exchange
terms) and Hartree Fock (including exchange terms)
6-Hartree-from-variation-incomplete.png
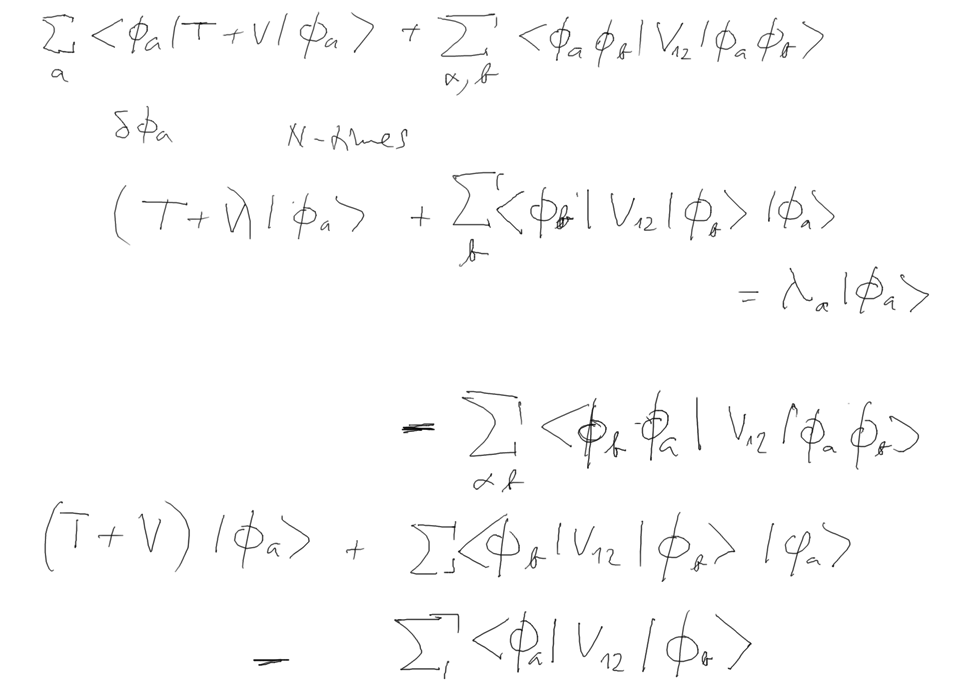
6-Hartree-from-variation-incomplete.png
So we start once more with more detail
PART 1 - without
considering exchange part
7-Hartree-from-variation-no-exchange.png
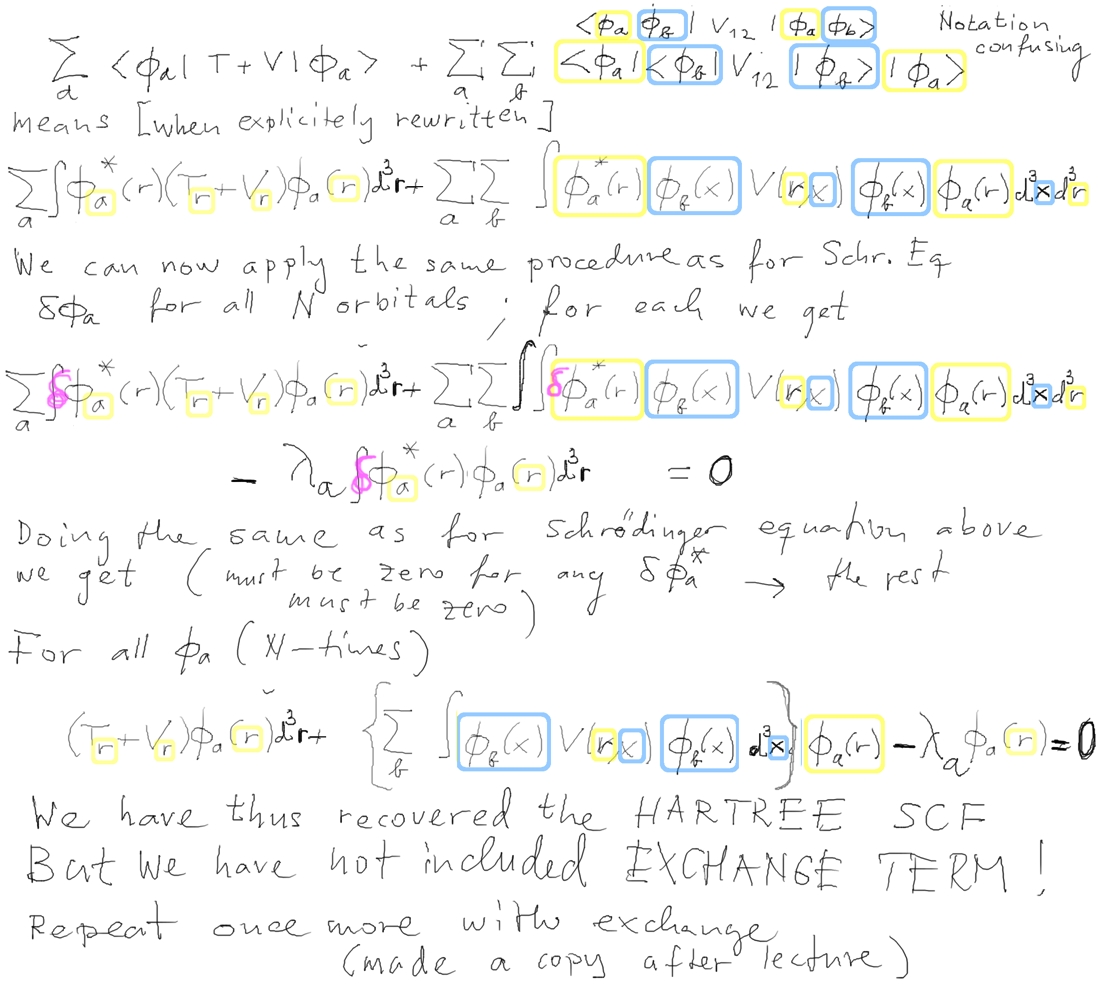
7-Hartree-from-variation-no-exchange.png
PART 2 - with the
exchange part included
... the formulae are copied and
extended
8-Hartree-fwith-exchange-variation.png

8-Hartree-fwith-exchange-variation.png
This is summarized in the following copy from the notes:
9-Hartree-Fock-variation-summary-nonlocal.png
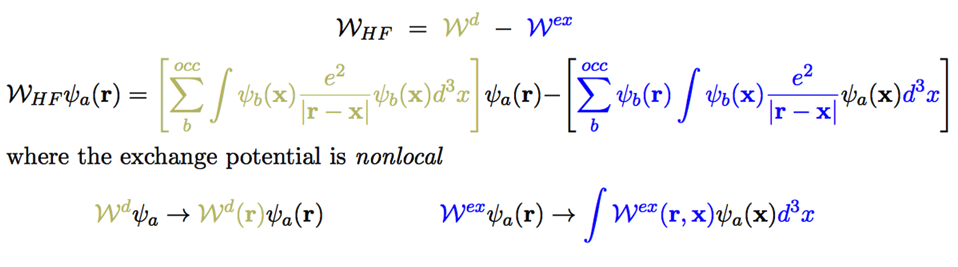
9-Hartree-Fock-variation-summary-nonlocal.png
Next time:
Non-local potential discussion
Total energy and the selfconsistent orbital energies
Starting the first part of physical optics