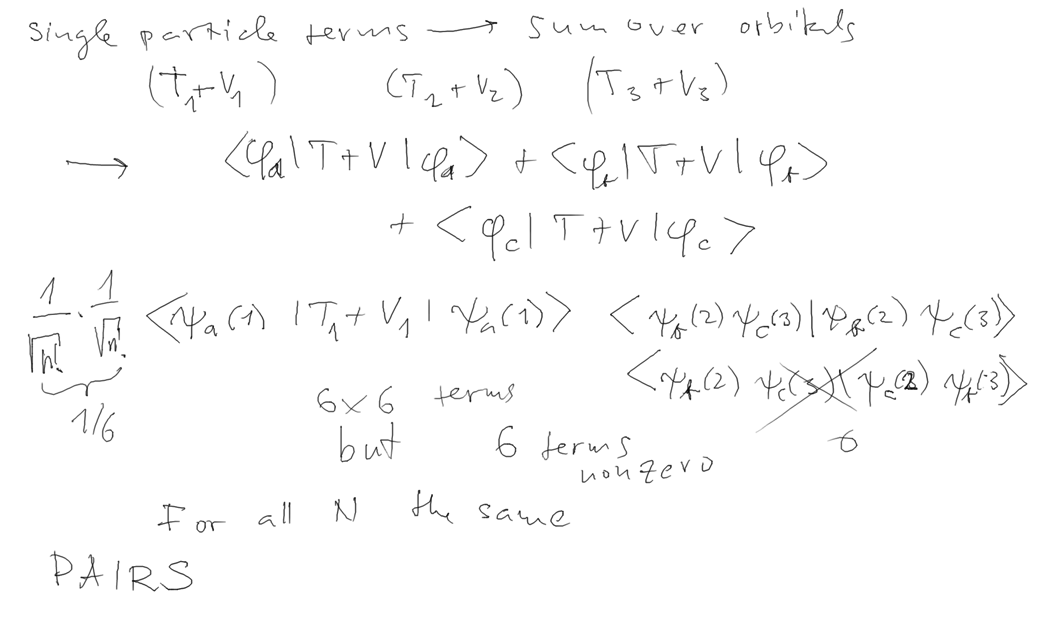Many Electron Atoms
SCF and DFT
The Self Consistent Field method we are now working with is in
recent time often replaced by
a method originating from chemistry: Density Functional Theory
In practice they are very similar - DFT in applications is based on
finding orbitals iteratively.
1_DFT_Density_Functional_Theory_vs_SCF.png

1_DFT_Density_Functional_Theory_vs_SCF.png
LINKS FOR DFT: Nobel prize in chemistry http://www.nobelprize.org/nobel_prizes/chemistry/laureates/1998/
wikipedia: http://en.wikipedia.org/wiki/Density_functional_theory
functional: http://en.wikipedia.org/wiki/Functional_(mathematics)
Qualitative and Quantitative applications of Hartree type
theories
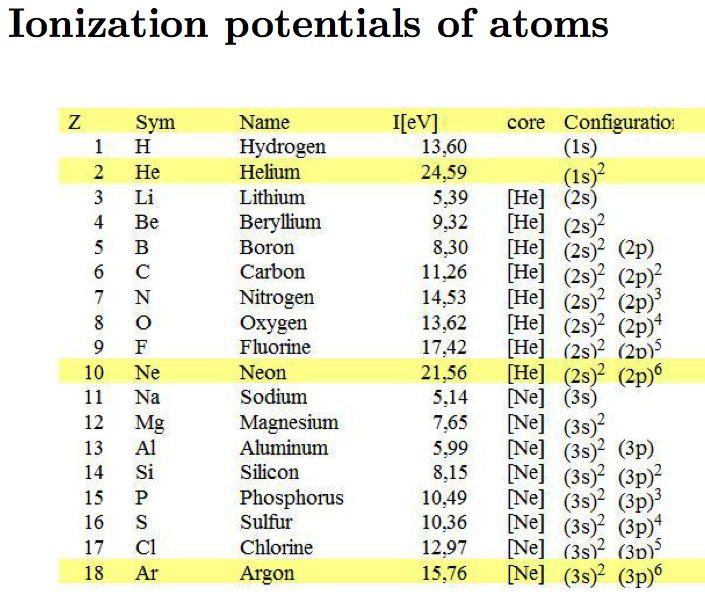
We shall look at systematics of ionization potentials and the
"electron configurations"
1b_Ionization_energies_tab.png
1b_Ionization_energies_tab.png
To understand the origin of (1s)2 (2s)2
(2p)6 (3s)2 (3p)6 filled
shell (the set (3d)10 does not make a shell)
we look at a model of the SCF
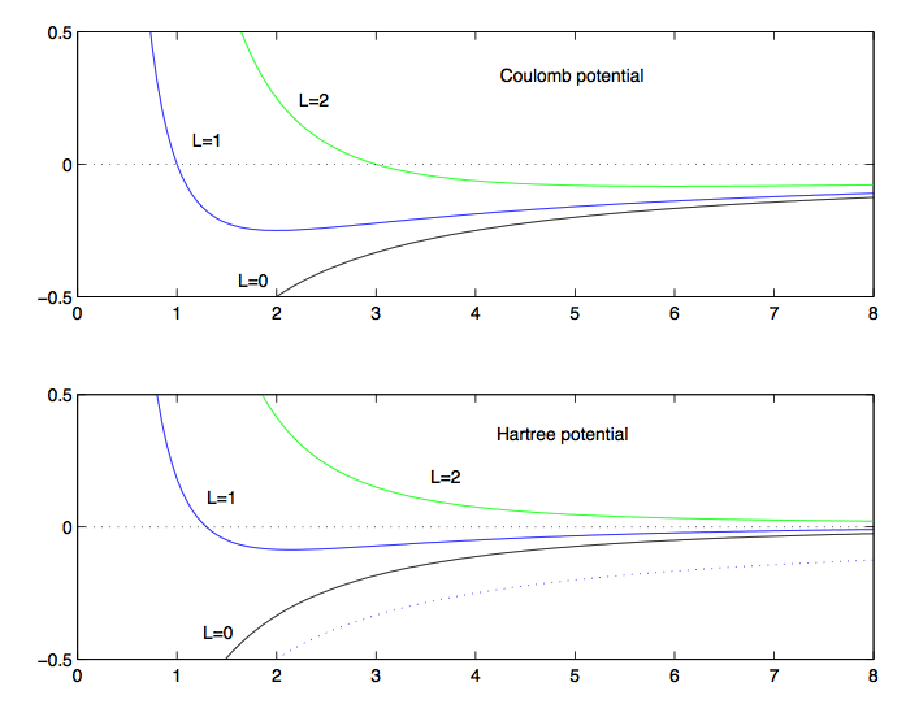
First the model: Radial potentials (including the centrifugal
barrier: (Screened Coulomb=model of Hartree )
The value of screening parameter alpha must be found empirically
(must be Z-dependent )

2__Coulomb_Centrifug_vs_Hartree_Centrifug.png
2__Coulomb_Centrifug_vs_Hartree_Centrifug.png
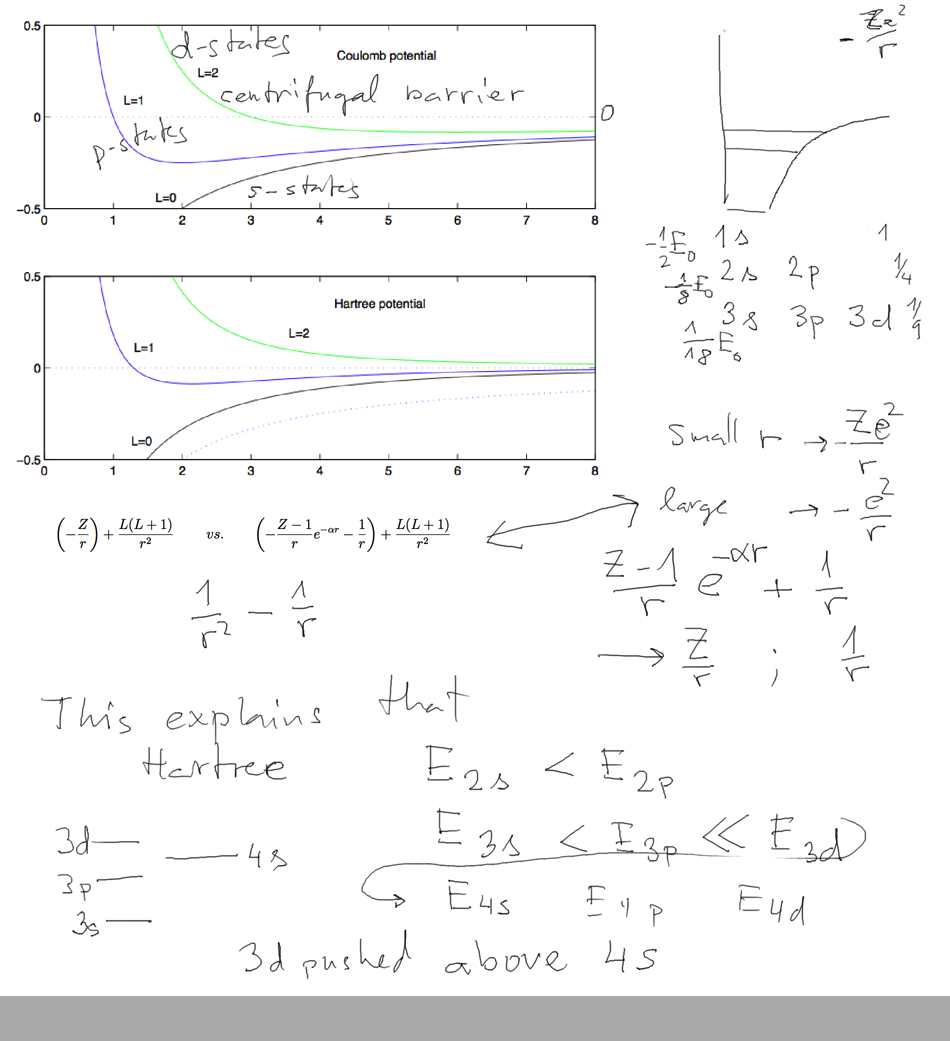
For Coulomb potential 3s 3p 3d have all the same energy.
For other potentials
this is not true
2_Coulomb_Centrifug_vs_Hartree_Centrifug.png
2_Coulomb_Centrifug_vs_Hartree_Centrifug.png
This drawing summarizes this point: the spectra of states
in Hartree-type potential have the
structur shown
3_states_n_l_in_Hartree_PERIODIC_TABLE.png

3_states_n_l_in_Hartree_PERIODIC_TABLE.png
Work with formal
derivation of Hartree and Hartree-Fock theories
We need to evaluate the expectation value of the total energy in the
SLATER DETERMINANT
(antisymmetrized independent particle - product state)
We started with revisiting the Helium excited state (done last time)
- here in detail, showing the
difference between single particle operators and pair-particle
operators
HELIUM ATOM ENERGY - as an example for Many=2
4_Helium_energy_Slater.png

4_Helium_energy_Slater.png
NEXT: 3 electrons,
LITHIUM ATOM ENERGY - as an example for Many=3
5_Lithium_description.png

5_Lithium_description.png
5_expectation_value_single_particles_and_pairs.png
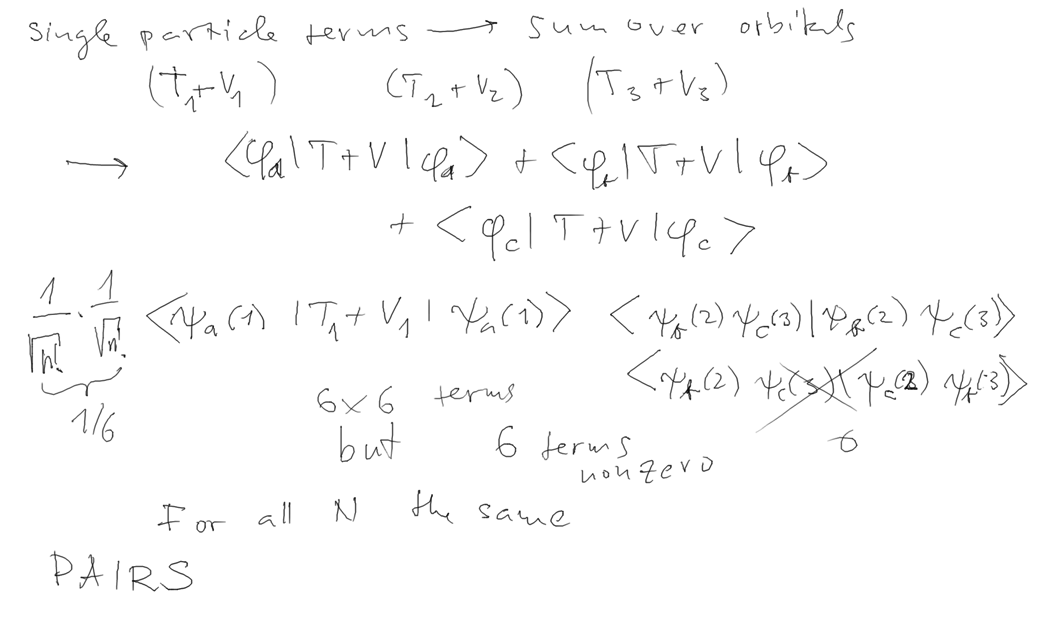
5_expectation_value_single_particles_and_pairs.png
5b_Lithium_terms_pairs.png
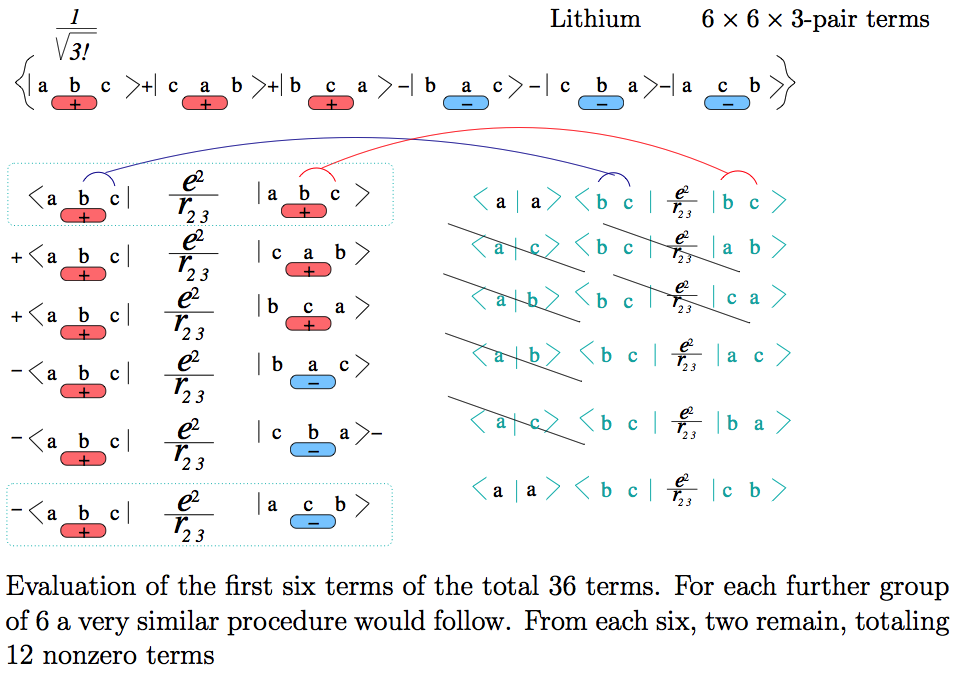
5b_Lithium_terms_pairs.png
We can generalize the result
(the pair interaction can be discussed in more detail)
9_Energy_Summary.png

9_Energy_Summary.png
This result will be used to
derive the SCF equations next time
Next time (following
our 2010 notes - PDF Many_Electrons_Atoms_2010.11.30.pdf
):
Pair interaction
result in more detail
Schrödinger equation from variational method
Variational
method - deriving Hartree-Fock Equations
Hartree-Fock
Equations
Total energy and
the selfconsistent orbital energies