PHYS261 23.08.2012 - About Quantum Mechanics
In the lecture we have looked at some basic techniques used in
quantum-mechanical work in atomic physics.
We use the computer screen to write as on the blackboard, and the
record of these writings are given here.
In addition to that, we shall add some notes, explaining roughly
what we have talked about.
The first topic is about what is really the main departure from
classical physics. First some few dates
and names, Planck, Einstein ....
Classical Physics = Newton Equations;
But Bohr, DeBroglie, Schrödinger.....
The trajectory x(t) (or in vector form) is studied in Cl. Mech., in
Q.M. the wave function.
Trajectories based on everyday experience of motion of bodies,
postulated by Galileo, Newton
Wave functions were based on observations and guesses, postulated by
DeBroglie, Schrödinger.
We try to sketch why and how
 1.png
1.png
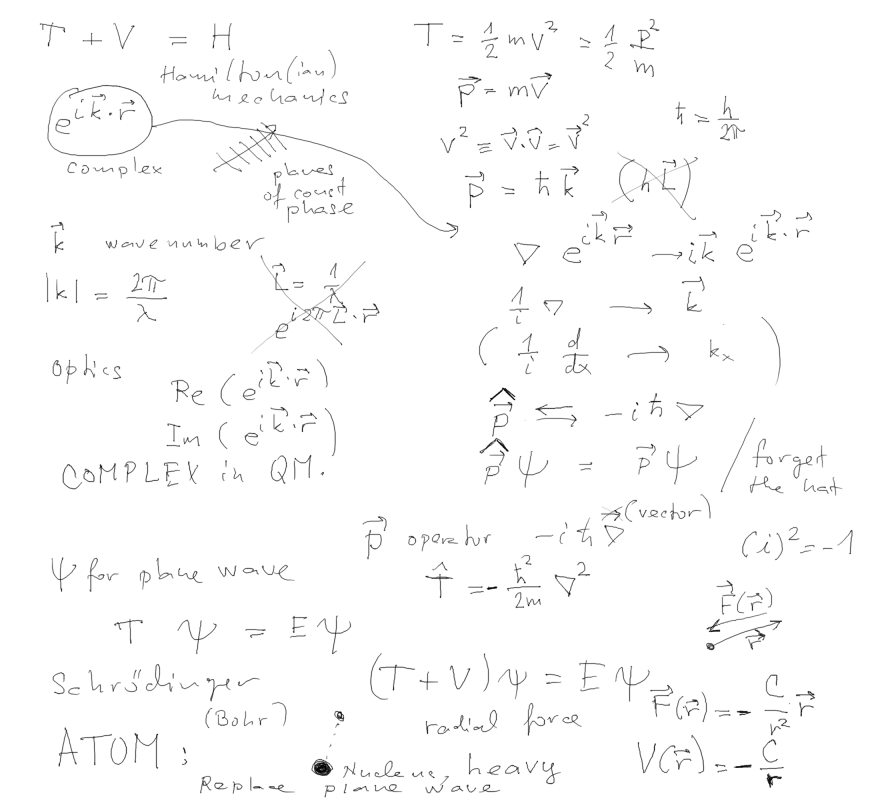
Differential equation in time from Newton; Mentioned Lagrange
Equations; Hamiltonian=total energy;
Calculus of variations (we shall meet later); waves - real part of
complex solutions
Waves in Q.M. - we need the COMPLEX values, not only real parts
In QM, physical variables get their OPERATORS. In this part we
illustrate how this was "guessed" and
later postulated. Originally, operators had "a hat" - as distinct
notation. Later the hats have been dropped,
mainly because of printing costs. We talked a bit about wavelengths
and wavenumbers.
 2.png
2.png
Schrödinger equation for the atom - Coulomb force and Coulomb
potential
Here: Only some total energies can give the Schrödinger
equation a "wave" solution.
Thes "waves" must be space limited, as also discussed in the next
slide.
Schrödinger equation also contains attached BOUNDARY CONDITIONS
(for whole space with boundaries in infinities, this results in
condition of "finite everywhere"
But first we looked at this board at the math of gradient, x,y,z
components etc.
 3.png
3.png
Numerical solution for MODEL 1-dim problems. Model: make the
Coulomb a regular function,
remove the singularity at r=0.
When starting numerical solutions, at x=0, they will "blow up",
become soon infinite
(work with Schrödinger Toy - we shall come back to it. Here are
two links:
http://web.ift.uib.no/AMOS/schroed/schroed_0.92.html
this is an older browser only - but not Internet Explorer -
with some explanations - recommended to try at this stage
http://web.ift.uib.no/AMOS/schroed/
- new version - which works on iPad,
iPhone, Android devices, touch, needs probably demonstration )
 4.png
4.png
Probability density interpretation of the wavefunction (Max Born
1927, the story - footnote giving Nobel Prize)
Here we also mentioned one feature:
Calculation of averages - over time and over space, "scanning" the
density of the trajectory visits.
Also this we should come back to later.
More about probability and statistics. Classical physics -
Statistical Mechanics, Physical Kinetics, basis
of thermal physics in modern formulations of thermodynamics
 5.png
5.png
Continuity equation, Probability density current in quantum
mechanics
This is important in transport, scattering -> PHYS264 in the
spring
One of the major features of quantum studies are the EXPECTATION
VALUES of operators.
In our applications we shall often calculate the expectation values.
Here we illustrated how they are related to probability densities
(below) - and again - the classical ideas.
But first, we mentioned some Math: Linear Algebra, Vector spaces,
Vector Spaces of functions
 6.png
6.png
And at the end - Matrix formulations;
Operators - Matrices; Wavefunctions -> vector of components on a
BASIS
This is just first mention; THIS WILL BE THE MAIN TECHNICAL TOOL in
our work - and we shall discuss it generally once more.
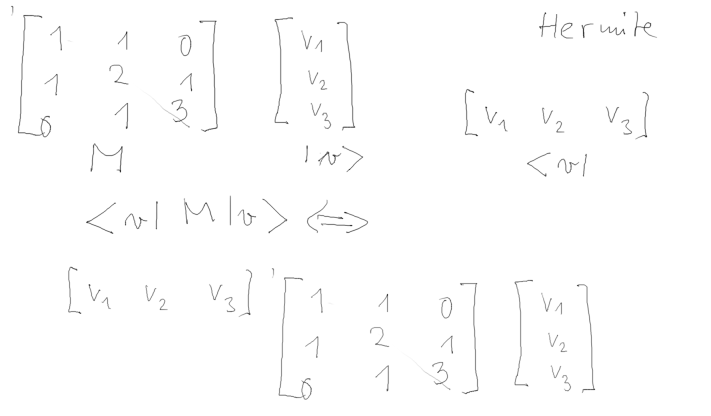 7.png
7.png
(work with Schrödinger Toy - we shall come back to it. Here
are two links:
http://web.ift.uib.no/AMOS/schroed/schroed_0.92.html
this is an older browser only - but not Internet Explorer -
with some explanations - recommended to try at this stage
http://web.ift.uib.no/AMOS/schroed/
- new version - which works on iPad,
iPhone, Android devices, touch, needs probably demonstration )
If you are interested, here are more links: http://web.ift.uib.no/AMOS/resonance/
and http://web.ift.uib.no/AMOS/schroedgallery/
 1.png
1.png  2.png
2.png  3.png
3.png  4.png
4.png  5.png
5.png  6.png
6.png 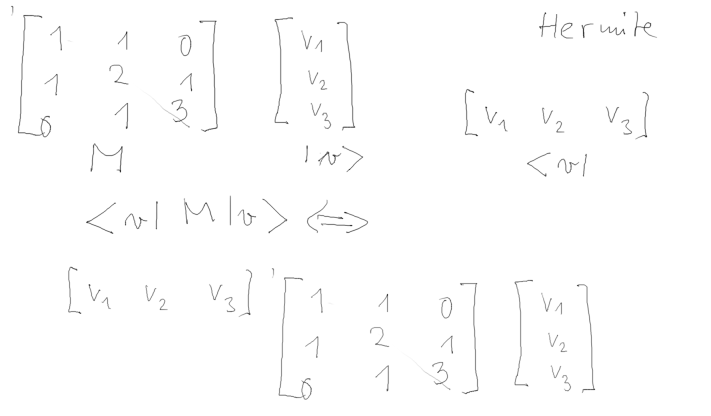 7.png
7.png