Helium (2-electron atoms). The role of electron repulsion.
Pauli principle and antisymmetry. Spin.
See also last year lecture at ../2011_09_01/
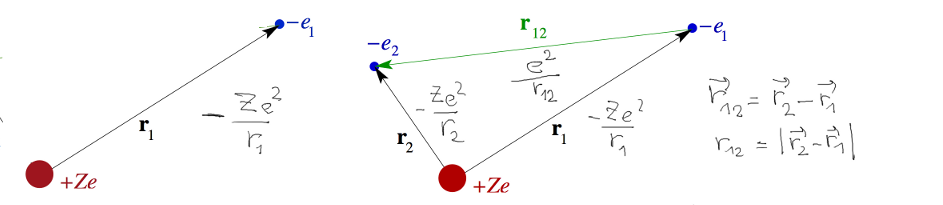
In the previous lecture we have set up the coordinate system and
identified the Hamiltonian -> Schrödinger equation
00-from-first-lecture.png
00-from-first-lecture.png
Here we discuss the expression: positive potential energy means
repulsion, negative means attraction.
(This is true for interactions which go to zero for large distance;
cf harmonic oscillator - attraction, but
energy positive. The "go to zero for large distance" is important
here.
Further we discussed the electron repulsion and sketched the independent electron approximation.
This means first ignore the repulsion -> product wavefunction
(both in 1s);
1-potentials-hamiltonian-helium-interactions.png

1-potentials-hamiltonian-helium-interactions.png
We shall go through a hierarchy of approximations sketched above.
First we explore the independent electron
approximation.
i.e. first ignore the repulsion -> product wavefunction (both in
1s);
Here we discussed the application; first the hydrogen-like
states for Z=2, no repulsion;
Then repulsion is added (we shall later justify the result that
repulsion adds 5/8 Z a.u.
We compared with experimental values - they are given by the two ionization potentials
(the 27.2/2 should be only 27.2, there is an error on the
board!!)
The expectation value of the repulsion is thus 34 eV.
This is a large improvement
from -108.8 eV to -74.8 eV - but this is still more than 4 eV above
the experimental value
To remember First ionization potential of Helium is 24.60 eV
The second one can gues - that is 2 times 2 times 13.6 eV, ie. 54.4
eV
2-simple-independent-electron-EXP-table.png

2-simple-independent-electron-EXP-table.png
We looked at the parahelium and orthohelium spectra. The excited
states must be mainly
- in the independent electron
approximation in (1s) (nl) product states (one
electron lowest, the other
excited to (nl), as 2s, 2p, 3s, 3p, 3d etc
But why are there two types, and why are the energies different?
7-parahelium-orthohelium_pp05.png
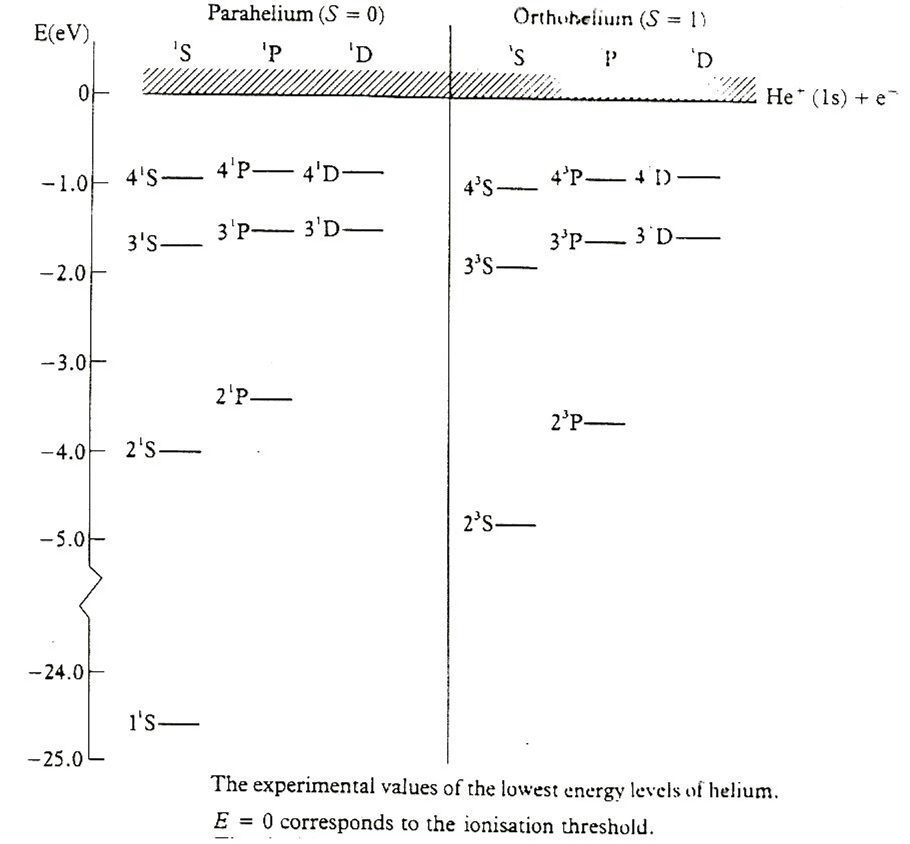
7-parahelium-orthohelium_pp05.png
independent electron
approximation in (1s) (nl) product states (one
electron lowest, the other
excited to (nl), as 2s, 2p, 3s, 3p, 3d etc
Independent, bot not quite, because when they are "identical", the
probability must be the same
if the two "identical" particles are swapped, exchanged.
(the product - independent particles - is now gone! - but they are
still "independent identical" - a new concept)
3_symmetry_to_exclusion.png

3_symmetry_to_exclusion.png
So there can be both fermions and bosons, antisymmetric and
symmetric wavefunctions
From identical particles and symmetry back to EXCLUSION
PRINCIPLE
there can not exist a wavefunction with two particles in the same
state!
4_symmetry_to_exclusion.png

4_symmetry_to_exclusion.png
there can not exist a wavefunction with two particles in the same
state!
But in the ground state we have (1s)(1s), as we repeated many times.
Both electrons are in the same state?? NO, their spatial behaviour
is the same;
But something must be different: THE SPIN
Spin is not angular momentum! It is rather a magnetic moment.
But there is a connection between angular momentum and magnetic
moment
We discussed spin properties; shortly
Then independent spin and space (Earth and Sun sometimes later,
forgotten at the lecture)
Product wavefunctions; Symmetry and antisymmetry for space and spin
INDEPENDENTLY
5_Spin_not_angular_magnetic_symmetry.png

5_Spin_not_angular_magnetic_symmetry.png
Product wavefunctions; Symmetry and antisymmetry for space and spin
INDEPENDENTLY
(this is added from one of the previous years ... - not at
this lecture )
6.-added-from-2011-or-so.png

6.-added-from-2011-or-so.png
This is the final result of this analysis;
Product wavefunctions; Symmetry and antisymmetry for space and spin
INDEPENDENTLY
This will be a starting point in explaining the
parahelium/orthohelium "mystery"
6_spin_and_space_independently_symmetrize.png

6_spin_and_space_independently_symmetrize.png
Helium from java applet at NIST (possible JILA, Boulder,
Colorado, or somewhere else in the US)
See also last year lecture at ../2011_09_01/
We can visit the
Atomic spectra Database at
8-He_I_Grotrian_java.png
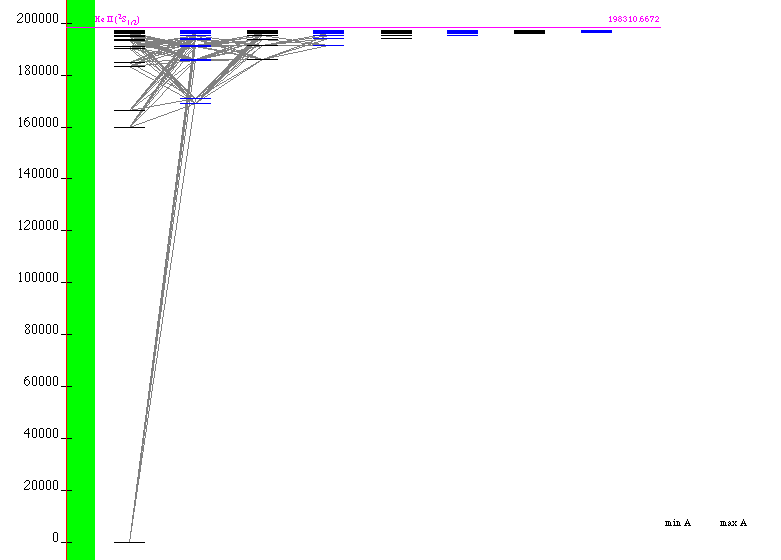
8-He_I_Grotrian_java.png
9-He_I_zoom.png
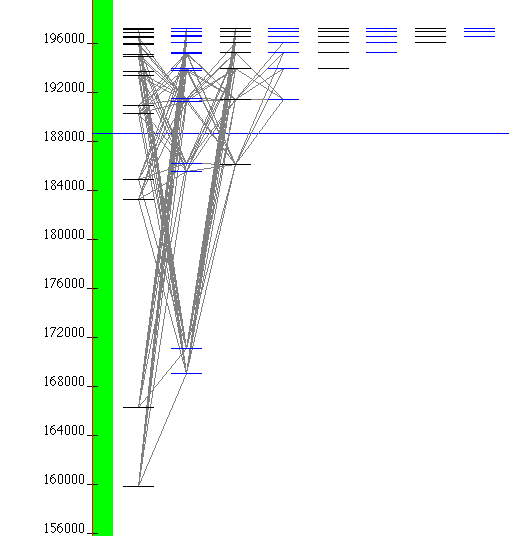
9-He_I_zoom.png
NIST-Database.png

NIST-Database.png











