Many-electron atoms - Hartree
- Selfconsistent Field - SCF
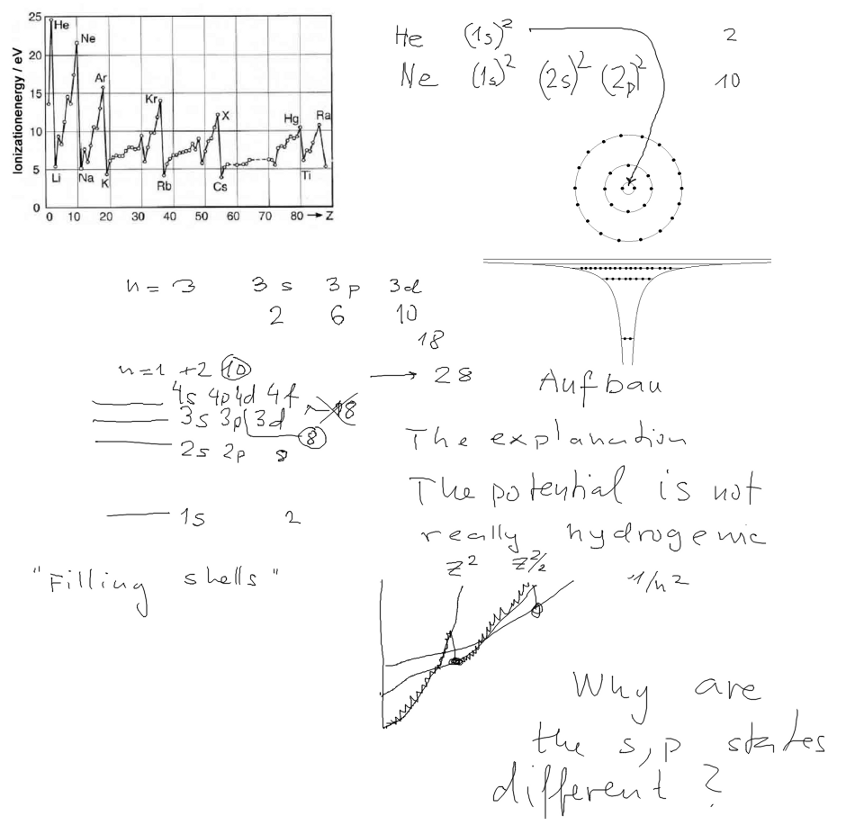
We start by looking at the experimental ionization potentials.
This term is another name for the binding energy of the 'last
electron', i.e. the
energy needed to ionize the atom (remove one electron).
We have seen the nature of this in the case of helium, in a sort of
dramatic fashion.
To remove one electron about 29 eV are needed. To remove the
remaining electron,
the hydrogen-like value, Z2 13.6 eV = 54.4 eV are needed.
The diagram shows the experimental values of ionization
potentials. It shows increased values for
Z = 2, 10, 18, 36, 54 .......
Simple consideration will show that the binding should be (somewhat)
increasing, but drop when a new
n number is started. SO the build-up principle should have "sudden
falls" of the potentials for values
Z = 2, 10, 28, ......
(each n has 2n2 orbitals, as one can simply show by
summing the (2 l + 1) up to (n-1) and 2 spins )
For hydrogen-like potential all these have same energy.
Why does it fail?
The atractive atomic field is simply not hydrogen-like.
We shall explain why
1_ionization-potentials-Build-up-principle-fails.png
1_ionization-potentials-Build-up-principle-fails.png
This is made by this matlab file binding2.m.txt
(the last model is quite complicated .... and "made up")
In the lecture we tried to explain the "drops".
Below is a little "game" using a simple quadratic increase of
hydrogen-like binding
(why not realistic? - the repulsion energies are not taken into
account)
In the third picture "filled shells" are included, but still no
repulsion ....
(These models are not really realistic, just meant to show "the
drops")
Last case is made up by trying to simulate continuously increasing
"screening"
(the observed "magic numbers" are used, not the hydrogen-based)
1.modelling.the_ionization_potentials.png

1.modelling.the_ionization_potentials.png
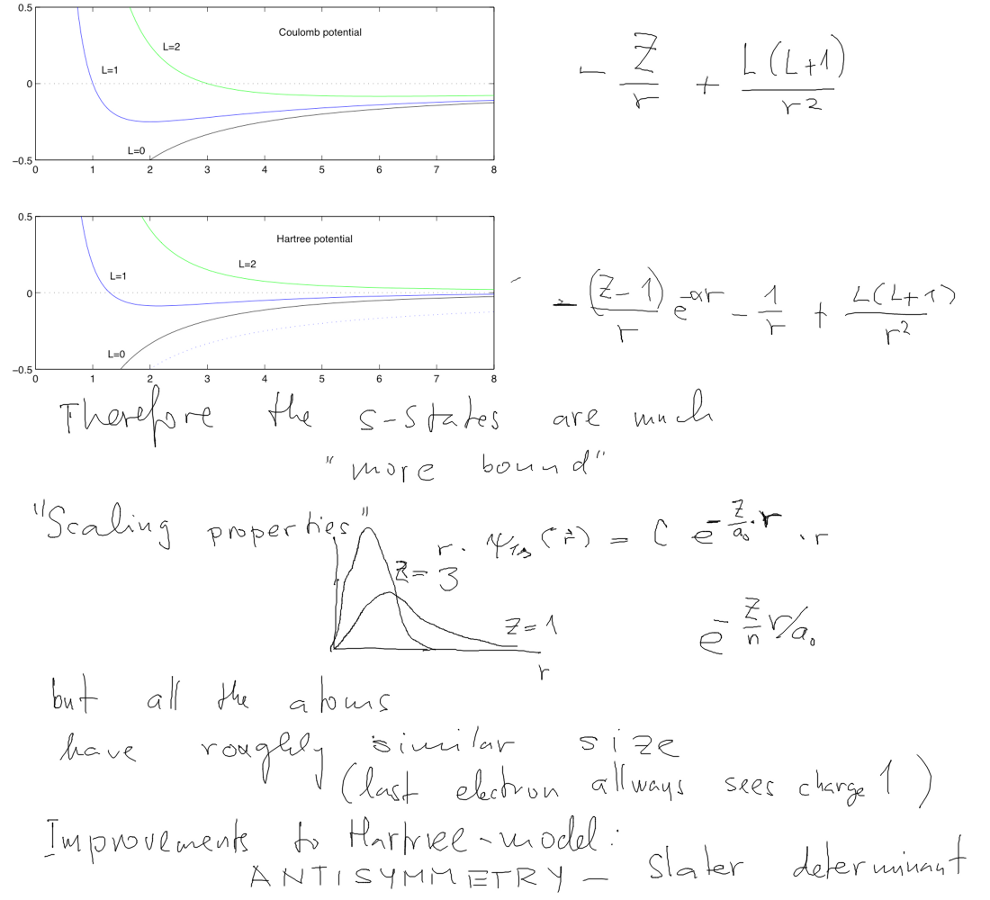
Below we will address the question why does the 4s dive below
3d, or rather why is the 3d pushed above 4s.
Now we start to explain the Hartree model of Self-consistent Field (
SCF)
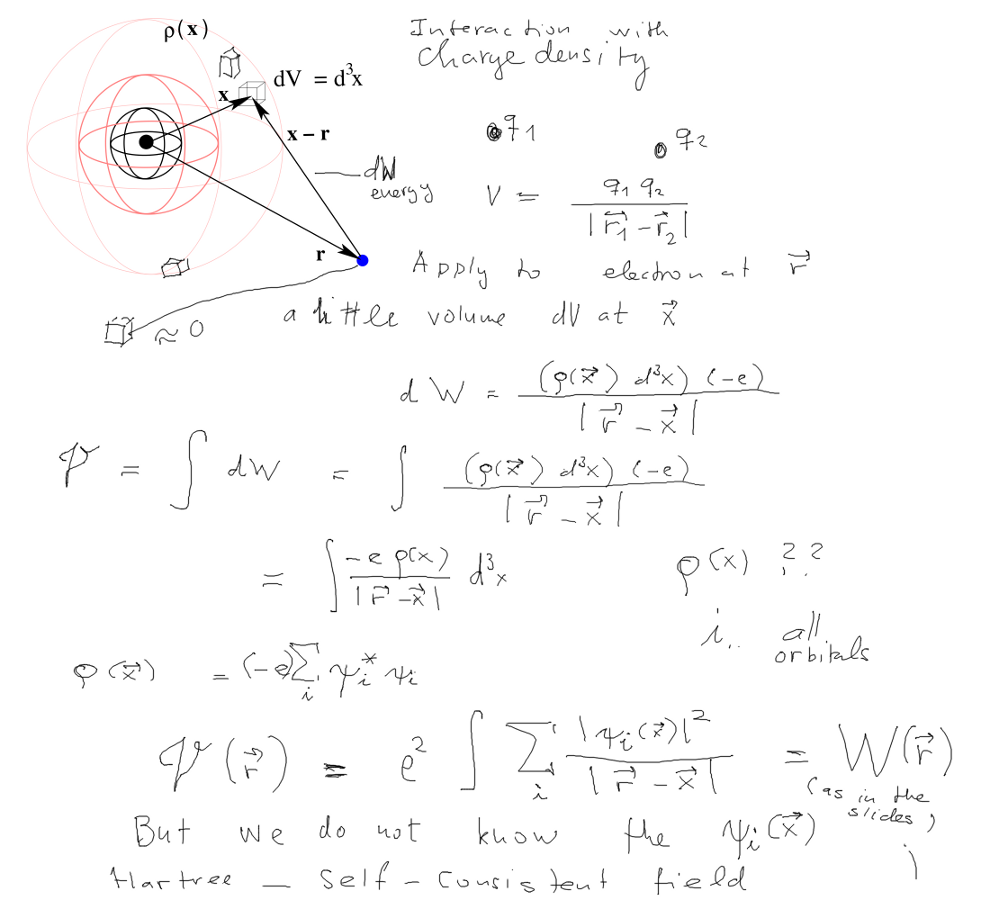
First - the electrons move in a potential made by the nucleus and
the "cloud" of other electrons
Cloud -> Charge density
2_electr_inter_with_cloud_of_charge.png
2_electr_inter_with_cloud_of_charge.png
Hartree model: independent electrons, each in "its orbital".
Product wave function
(we have discussed this in helium case ... )
Hartree did not know about the antisymmetry. Just used the "Pauli
principle" as in "buil-up principle".
( antisymmetry will come later; Slater determinants, Hartree-Fock
method )
Historical: Hartree worked on these models since about 1926;
published numerical calculations
made on a mechanical calculator together with his father (Hartree
and Hartree) )
3__Hartree_model_iteration_self_consistent.png

3__Hartree_model_iteration_self_consistent.png
Here we have shown the iteration; Chain of approximations
Repeating this chain until it produces SELF-CONSISTENCY
How do we know that it will converge?
1. Allways takes N (or rather Z) lowest energy orbitals.
2. The approach to the "real minimum" as the theorem we used in
variational method
3. We must not start "too far" - so the hydrogen-like start is not
really recommended
(what could happen? Mainly "jumping" over the
minimum )
The practical procedure used was to start with Z=2, use the
resulting potentil as start
for Z=3, use the resulting Z=3 pot. as start for Z=4 (i.e. starting
point - use the potential
to generate the orbitals.
(we have seen "jumping" in some cases, i.e. oscillation back and
forth .... )
4_Self-consistence-and
modelling-the-potential.png

4_Self-consistence-and
modelling-the-potential.png
A screened model potential which should in principle model the
effect of electron screening.
The over-all attractive field felt by all electrons - when they are
closed to the nucleus, it is
the nuclear charge.
When far away, it only "feels" the charge one, all the other
electrons screen the nuclear Z
And here is the explanation of the s-states (and p-states)
lying lower than the d-states
5_model_potential_with_centrifug_barrier_explains_4s.png
5_model_potential_with_centrifug_barrier_explains_4s.png
Next time - also exercise with computing - see ../2010.10.14/





