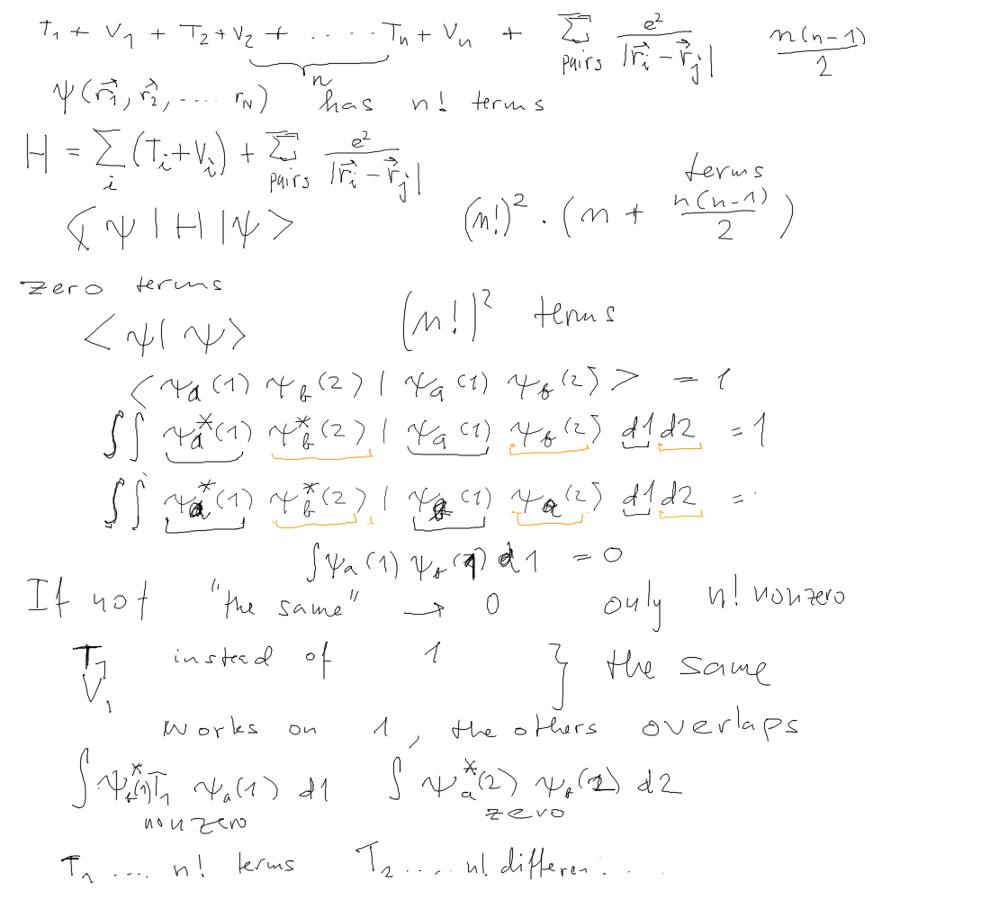N particles - energy - And new variational method
Antisymmetric product wave-function for N particles is realized
by a determinant of N x N matrix
constructed by taking the N-wavefunctions different for each
column and the coordinates different
for each row
(or opposite, functions in rows, coordinates in columns, the
determinant will be the same)
Connection of determinants to permutations; general definition of
determinant;
(Comment: Determinant antisymmetric - two equal columns give
zero; Pauli principle
re-gained; Symmetric analogue of determinant - permanent http://en.wikipedia.org/wiki/Permanent
)
1_determinant_Slater_wavefunctions.png

1_determinant_Slater_wavefunctions.png
In this connection this determinant is called Slater Determinant
after
John C. Slater
Evaluation of EXPECTATION VALUE of the total energy for a slater
determinant
Counting the terms
For one-particle operators (functions of 1 variable only) this
counting
is quite straightforward
First we start by taking only the scalar product. We see the
consequences
of the orthogonality of the orbitals
2_evaluate_expectation_values_1_particle_2_particle.png
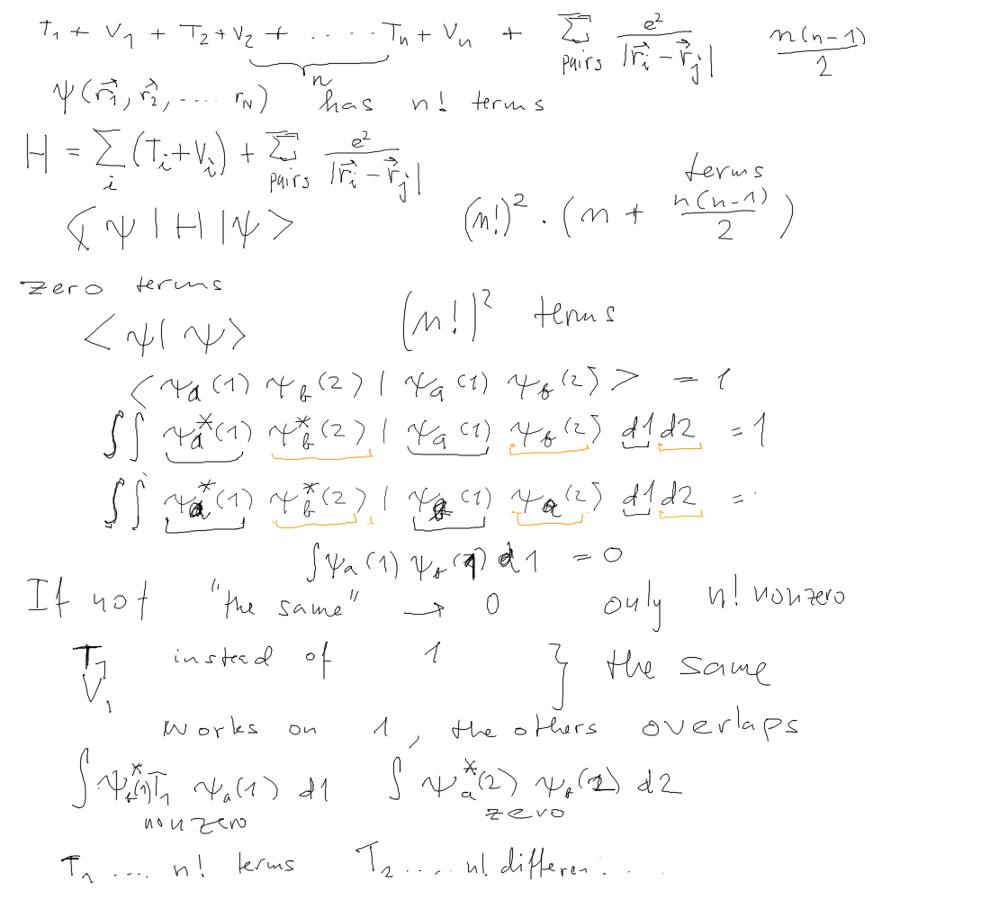
2_evaluate_expectation_values_1_particle_2_particle.png
For one-particle operators (functions of 1 variable only) this
counting is quite straightforward
see the above the scalar product. We see again the consequences
of the orthogonality of the orbitals
3_one_particle_orthogonality.png

3_one_particle_orthogonality.png
1-particle operators: SUM OVER PARTICLE COORDINATES
transforms to SUM OVER ORBITALS
We look at the N=3 case explicitely; 3 different particles and also
three PAIRS
And the Slater determinant has 3!, i.e. 6 terms
4_1_lithium-example.png

4_1_lithium-example.png
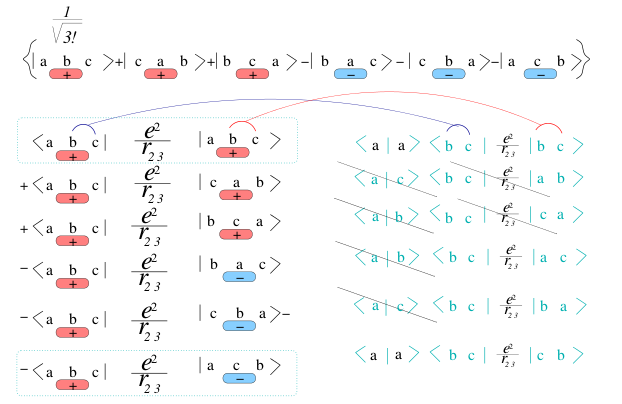
Calculating the expectation value, we will have for each term in
H 3! x 3! = 6 x 6 =36 terms
Here we look at the pair operator V(i,j), for V(2,3) and look at the
first 6 terms
(color-coding of +/- terms)
we see the consequences of the orthogonality again
4_2_Example_Lithium_6_of_36_terms.png
4_2_Example_Lithium_6_of_36_terms.png
The result for N-particle operation without antisymmetry is
simple:
There is only one term from wavefunction product (no Slater)
but the sum over coordinate pairs
Clearly,
2-particle operators: the SUM OVER COORDINATE PAIRS becomes
SUM over PAIRS OF ORBITALS
for a product wavefunction
THE SAME FOR SLATER???
4_two-particle-operators.png

4_two-particle-operators.png
5_3_energy_Summary.png

5_3_energy_Summary.png
We have thus evaluated the total energy expectation value
summary:
1-particle operators: SUM OVER PARTICLE
COORDINATES transforms to SUM OVER
ORBITALS
2-particle operators: the SUM OVER COORDINATE PAIRS becomes
SUM over PAIRS OF ORBITALS
It is a "function" of the orbitals; This type of dependence
FUNCTIONAL
5-energy-energy-functional-variations.png

5-energy-energy-functional-variations.png
FUNCTIONAL, Functional derivative, variation; Calculus of
variations; variation (analogue of the differential)
variation (analogue of the differential); Functional
derivative,
HOW TO GET SCHRÖDINGER EQUATION from a condition of
extremum
- remember the theorem:
The ground state energy is a minimum of all possible expectation
values
As a functional it has thus minimum
The variation (analogue of the differential)
6_Functional_derivative_does_not_give_Schroedinger.png

6_Functional_derivative_does_not_give_Schroedinger.png
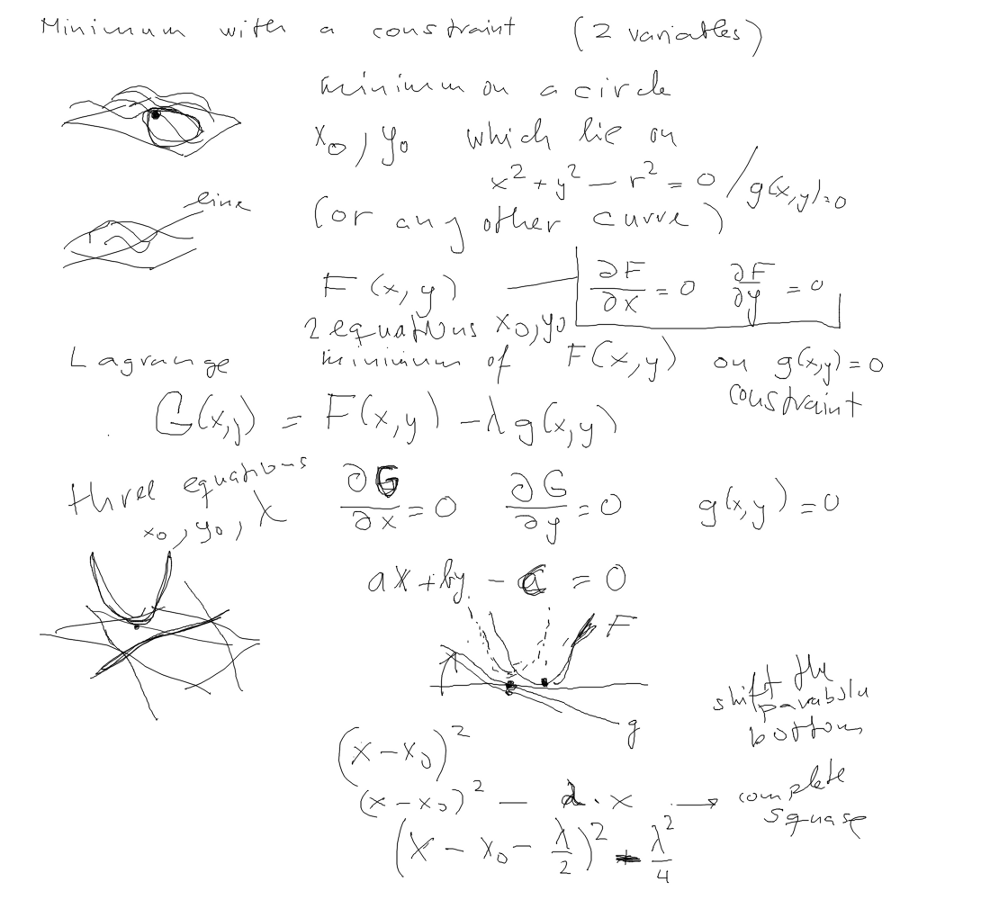
This would not work - thus MINIMUM WITH A CONSTRAINT
MINIMUM WITH A CONSTRAINT - functions of 2 variables, minimum on
a curve
as example - Lagrange multipliers
7_Minimum_with_Constraint-provides_Schroedinger.png
7_Minimum_with_Constraint-provides_Schroedinger.png
Summary from the presentation
8_Schroedinger_reviewed.png

8_Schroedinger_reviewed.png