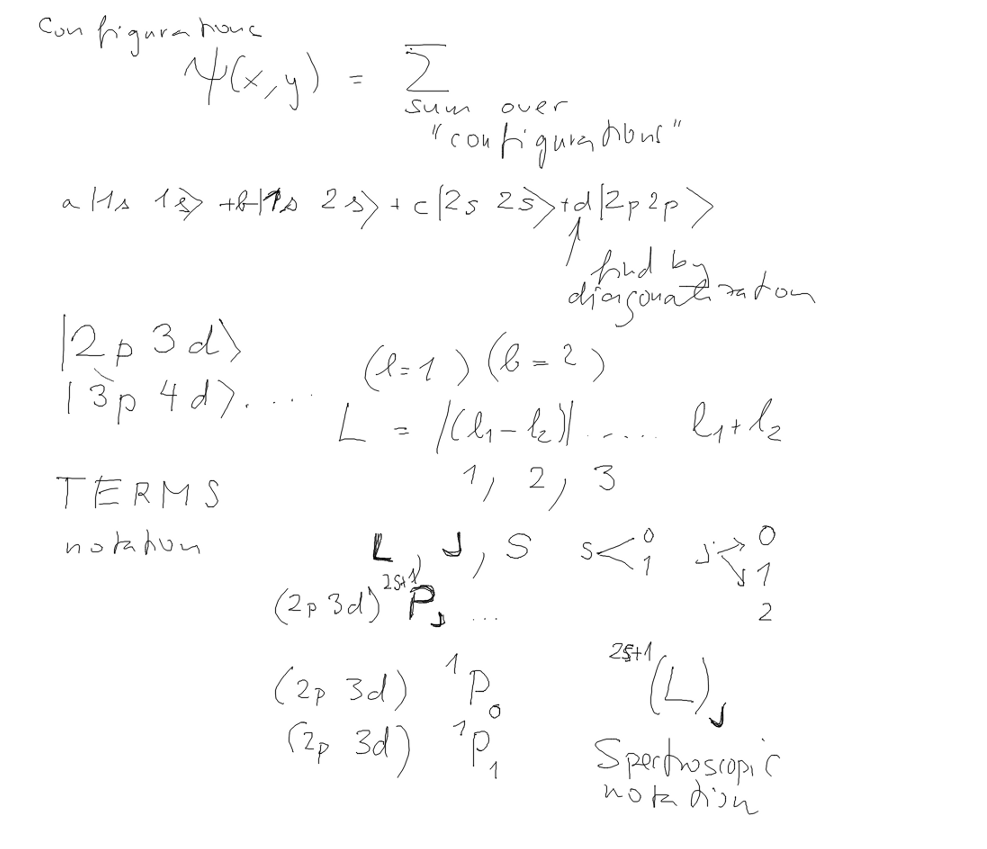| Hartree-Fock: The total energy and sum of orbital energies Configuration Mixing Spectroscopic Terms |
For the PROJECT WORK - LINKS:
SCF-Herman-Skillman-Exercise.html The zip-file of the code and basic instructions are at this address: ../2010.10.14/ ( Mac OSX - 2009+, Windows, Linux ) 1997 Project: folk.uib.no/AMOS/Hartree/lindex.html folk.uib.no/AMOS/Hartree/ |