
3_angular_momentum_VILVITE_tech.jpg
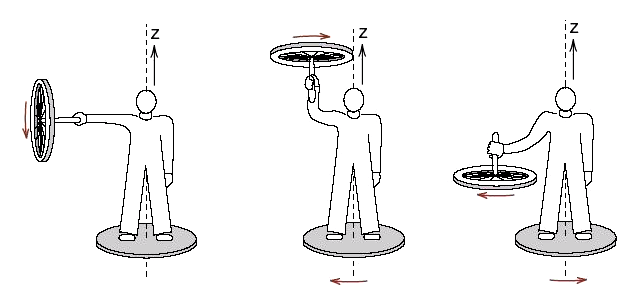
Rotating-platform-Bicycle-Wheel.png
 Rotating-Stool-Bicycle-Wheel.jpg
Rotating-Stool-Bicycle-Wheel.jpg
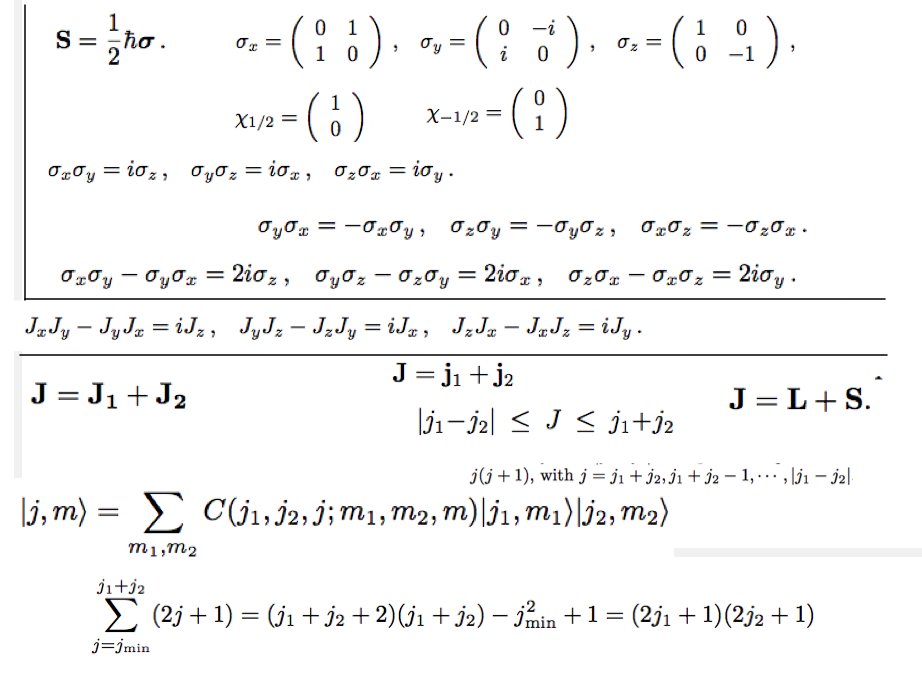
3_angular_momentum_VILVITE_tech.jpg
 3_angular_momentum_VILVITE_tech.jpg  Rotating-platform-Bicycle-Wheel.png |
 Rotating-Stool-Bicycle-Wheel.jpg
Rotating-Stool-Bicycle-Wheel.jpg |




