Many
Electron
atoms
-
part
4
SCF - computing project
-
at
the
end of the page
Nonlocal exchange potential
SCF - computing project
-
at
the
end of the page
In the previous lecture we arrived at the Hartree-Fock equations and
noted that the exchange potential
is
nonlocal - here is an
illustration
xcf_0000.png

xcf_0000.png
So what does it mean nonlocal potential.
It does not have a simple counterpart in the classical mechanics
The closest could be interaction with an extended object - with some
type of a "tail" or "cloud" around itself
Quantum mechanics - first we look into relation between the
formal Dirac representation
and the wave mechanics - and we find out that local operators
though natural in wave mechanics - are sort of exceptional in the
formal settings
The locality is "assured" by an extra delta-function
This is done via the expansion -> from there THE IDENTITY OPERATOR
as sum over projectors | a > < a |
( summed over all a in the complete set )
Including the continuum spectrum - and of the states describing
"localization" in one point (un-physical; uncertainety )
xcf_00.png

xcf_00.png
So non-local operations involve sampling of the effect over the
whole space
The exchange part of the potential is a nice example of the nonlocality
The nonlocal potentials are in some connections sometimes called also
velocity-dependent
That is because the dependence on the other coordinate could be
attempted to be represented through expansion
over the distance between the two coordinate points - and that could be
done via Taylor expansion
- that would lead to derivatives at the first point - and the gradient
operation is connected with the momentum operator
In classical mechanics the momentum is most often connected with
velocity
xcf_01.png

xcf_01.png
Nonlocal potentials are difficult to work with.
Approximate methods, or rather simulations of the nonlocality are often
used. Complicated, but established procedures
Density Functional Theory DFT is nowadays more
popular SCF method than the Hartree Fock method
http://en.wikipedia.org/wiki/Density_functional_theory
The SCF procedure is very similar, but the theoretical basis is
different
CHEMISTRY
Self-consistent fields remain in principle single particle methods,
product functions (products of orbitals)
Electron correlations are mainlyleft out
DFT includes also a simulation of correlations - but necessarily in the
single orbital picture
So what is there beyond SCF - that leads to configuration
mixing
-
see
below
xcf_02.png
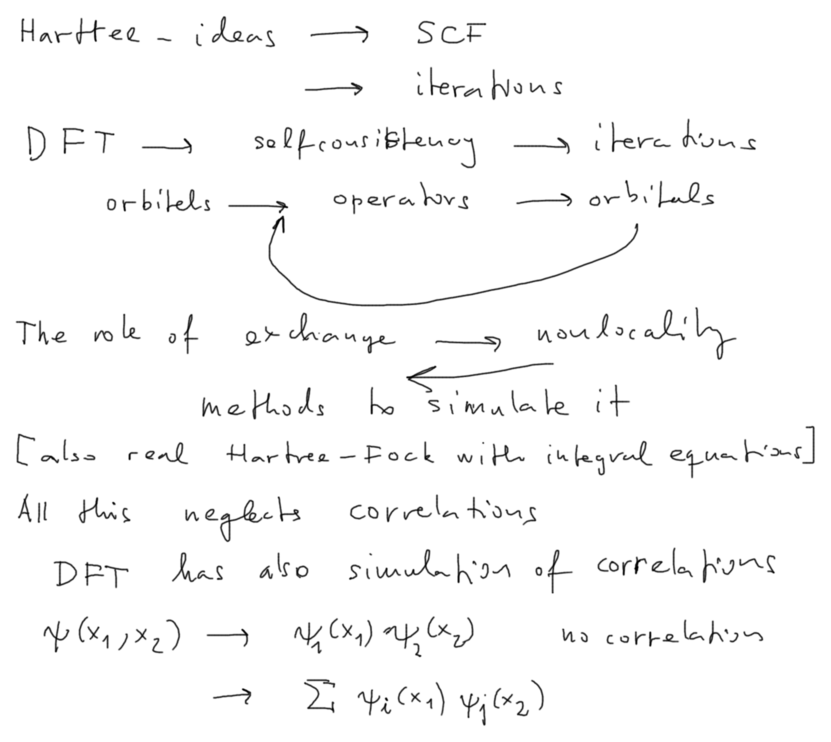
xcf_02.png
Correlations ----
What is there beyond SCF the correlated more-particle functions -
that leads to configuration mixing
- see below
Connection between
the many-electron total energy and the sum over the orbital energies
Orbital energy - the "Lagrange multiplier" of the orbital condition
If W is the electron repulsion - it is of the form W(x,y) - thus the
matrix element involves integration over
two space variables (i.e. six, as is clear)
So in the Hartree-Fock equations and generally during last parts of
this course there always remains one
"naked" coordinate - as here when we write < b
| W | b > - it is still a function of the
other coordinate
xcf_04.png

xcf_04.png
So the total energy is not simply a sum of the orbital energies
To get the
total energy, we can sum the orbital energies, but then we must
subtract the whole
repulsion
energy in the system, since it has been counted twice
Particle correlations -
and Configuration mixing
Here we show that when we abandon the independent particle - i.e.
product wavefunctions
the natural application of the expansion theorem N times (here for 2
coordinates - twice )
leads sort of automatically to multiple sum over products of "orbitals"
This is often called configuration mixing - one product
term is called one configuration
xcf_05.png

xcf_05.png
SCF - computing project
Short presentation of our computing project .... links to some
preliminary readings below the slide
xcf_03.png

xcf_03.png
SCF - computing project
Links to preliminary reading
-
and
first computing
tests
These links are supposed to open in new
window
or
tab
Very brief last link (2011) ../2011_09_27/second-lecture.html
Detailed link including the zip-file for download (2010) ../2010.10.14/
Direct link to the 1995 files (updated link 2019) https://folk.uib.no/AMOS/Hartree/






