In this lecture we mainly derive the Hartree-Fock equations from a version of variational principle
END LAST LECTURE: variational derivation of self-consistent field based on the discussed "trick"
Schrödinger eq. from variational method
applied to the
Expectation value of total H in the Slater determinant
Such variational method gives N Schrödinger - like equations for N orbitals
This will be done using the method which we will re-visit below
We start by the sort of summary - apply the Lagrange multipliers for EACH of the extra normalization condition of
EACH of the orbitals - see the inter-changed notation - by | alpha > we denote | psi_alpha > and vice versa
Now the variation of the product N-electron product function - sum of all variations for each of the orbitals
But then the zeros must be true for each delta-alpha independently - we get N independent equations

500_variation_Schroed_Slater_expectation.png
We re-visit the Schrödinger variational method from the last time (see also next time)
Hartree-Fock continues two slides below
The following slide has been added from the "future" - additional discussion in the 2015_10_15 next lecture note
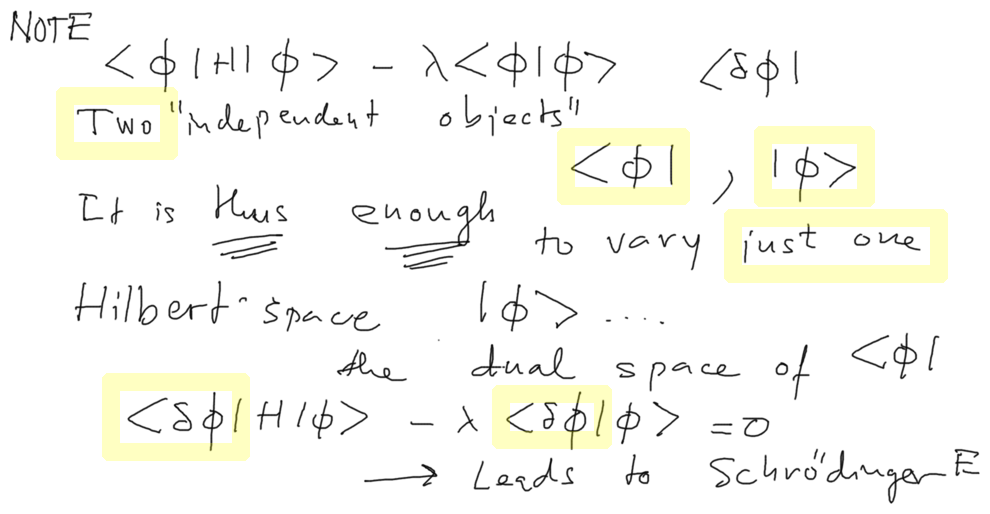
1000_note_on_variation_Only_bra_vector.png
We re-visit the Schrödinger variational method from the last time (see also next time)

503_variation_Schroed_Slater_expectation.png
Hartree-Fock continue:
Two slides above: the variation of the product N-electron product function - sum of all variations for each of the orbitals
But then the zeros must be true for each delta-alpha independently - we get N independent equations
In each equation there will be a "direct part term" and an "exchange part term"
Note the somewhat unclear notation: we make matrix elements "integrated over one variable only"
i.e. they remain FUNCTIONS of the other variable
(there should be a different "bra and ket" e.g. round ( | V | ) )
schematically
G(x) = integral dy psi( y) V(x,y) psi(y) --> G(x) = ( psi(y) | V(x,y) | psi(y) ) --> G(x) = ( psi | V(x,y) | psi )
but we use for simplicity G(x) = < psi | V(x,y) | psi >
WIth this in mind, we see that the exchange term behaves in a strange way
while the direct term leeds to the Hartree result

510_deriving_Hartree_and_Exchange.png
Summary of the Hartree - Fock from the presentation

513_deriving_Hartree-Fock.png
See below the explicit form (in terms of integrals) of the Hartree - Fock equations

515_deriving_Hartree-Fock.png
What is a local or non-local potential?
We show how local operator emerges from an abstract operator
completeness relation
Sum | i > < i | = Unity ---> Integral | x > < x | dx = Unity
and < x | x' > = delta ( x - x' )

520_what_is_non-local-potential.png
Most operators in elementary systems are LOCAL
.... but there are some non-local operations ( Green's function operator, for example; not in this course )