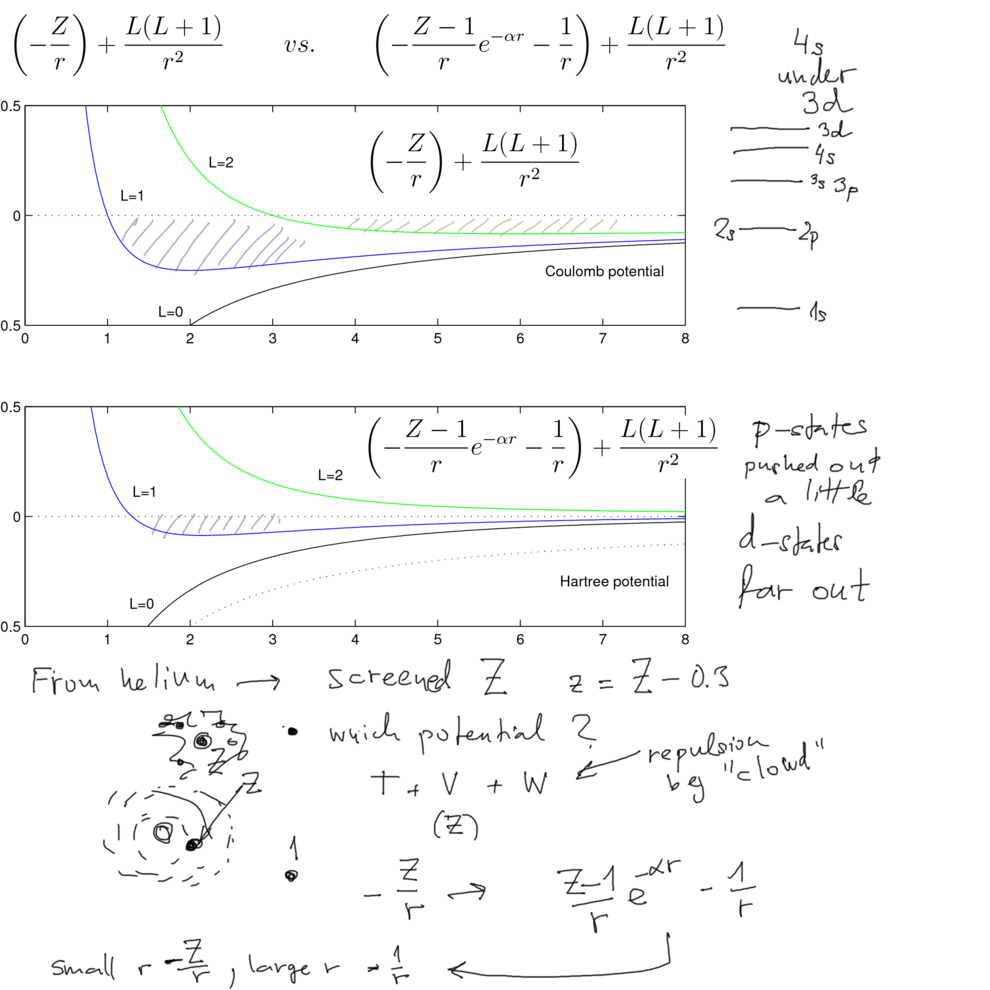
1. The problem from the last lecture: why are the energies not as for H-like atom, depending only on n (4s under 3d)
2. Evaluation of < Phi | H | Phi > for Slater determinant, starting by product function
3. Towards the variational derivation of the selfconsistent field
Energy eigenvalues of the Nucleus + Cloud potentiuals
For H-like atom, the energy eigenvalues are depending only on n; In reality, the state 4s has lower energy than 3d.
Is it possible to explain this in simple terms? Is it systematic?
We model the "cloud" by a simple "screening"
for large r, the electron only feels z=1
for r close to 0 - the cloud effect is small, the full charge Z
the simple formula with the exponential reduction has this property
Further, the radial equations contain the contribution from the angular part (centrifugal barrier)
The figures show clearly that the L > 0 states are "pushed outside", especially the L=2 and larger
Therefore these will be less bound
Simply, the presence of the other electrons is responsible for the systematically reduced binding
of the d-states (and higer L)
10010_Hartree_vs_Coulomb_Periodic_Tab.png
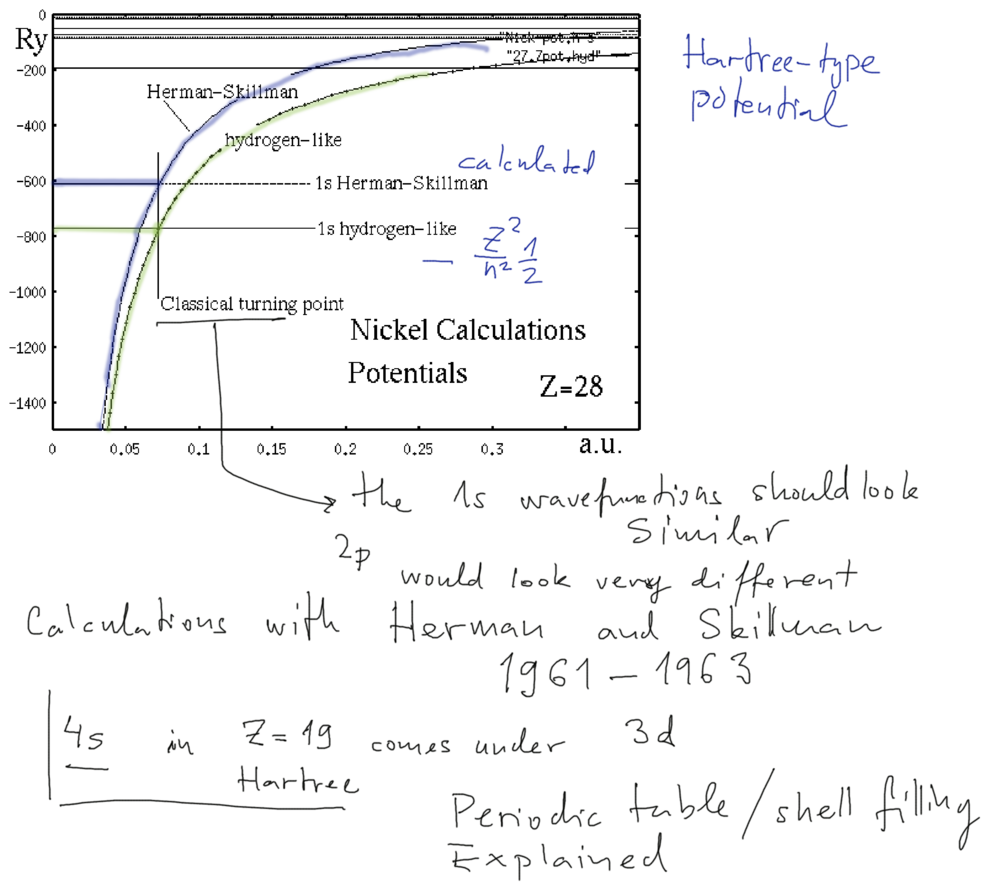
Calculated potential from the Herman - Skillman code (numerical exercise )
The above discussed behaviour is confirmed (the analytical model is a reasonable
representation of the numerical results )
10030_Hartree_potential_calculations.png
Many - Electron Atom - Independent electrons - Slater determinant
Evaluation of the total energy expectation value
Determinant - mathematical object from linear algebra
Has accidentally "symmetry" properties needed for Pauli - principle obeying functions ( exchange "symmetry" )

10100_SLater_Determinant_1.png
Slater determinant - applying determinant definition to product wavefunctions
Exchange of "particles" - swapping of columns - gives + or -

10110_SLater_Determinant_2.png
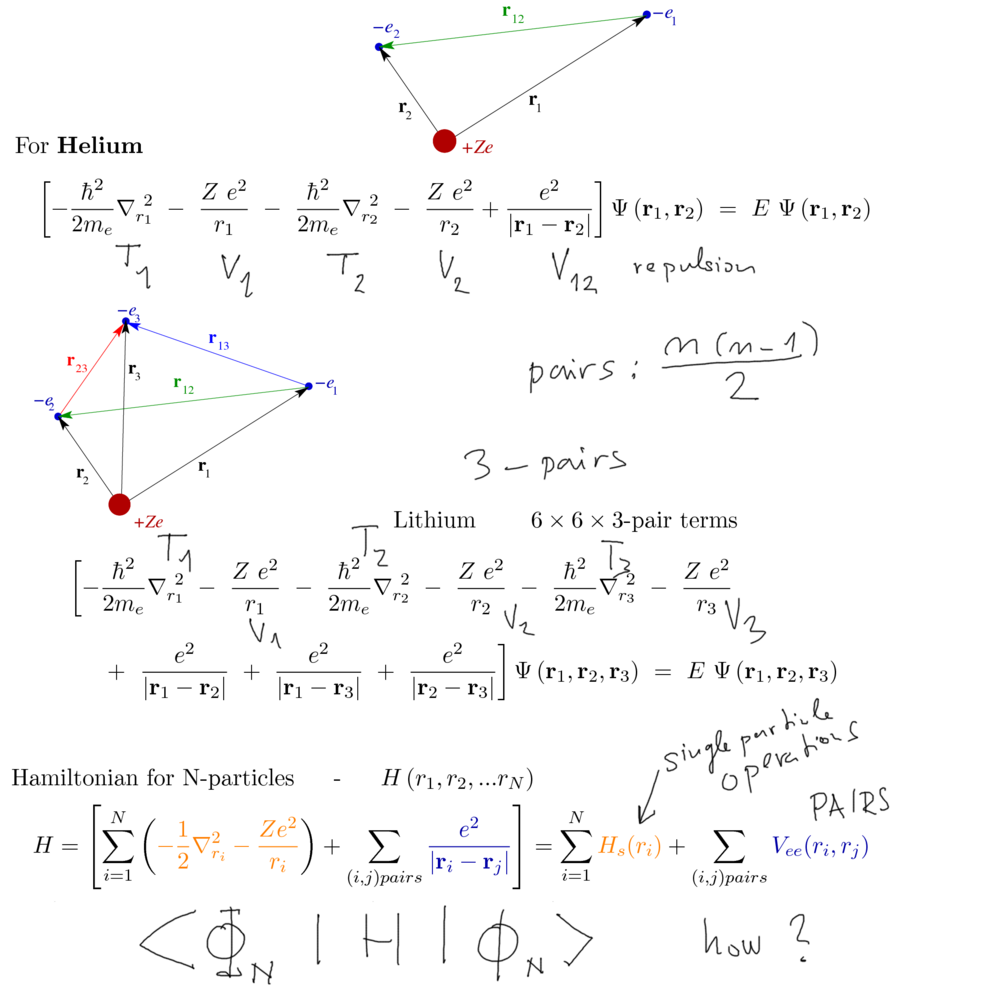
Total energy for He and Li - Li is the first "many-electron" N=3
He one pair Li 3 pairs N (N-1) / 2 pairs
Also, there are N single - electron terms
Sum over coordinates ( singl-electron terms) and sum over pairs of coordinates
10120_Helium_and_Lithium_first.png
What shall we see - details are seen on the printed frames discussed below

10150_More_than_3_particles.png
First we evaluate the expectation value for a simple PRODUCT function ( Slater determinant has N! such products )
1) the product function is normalized
2) it is easily seen that the following is true
The sum over coordinates --> sum over the involved orbitals
The sum over pairs of coordinates --> sum over pairs of orbitals
first - sum over coordinates --> sum over the orbitals

A10_Energy_N_particles_Product_only.png
second part PRODUCT function
sum over pairs of coordinates --> sum over pairs of orbitals

A20_Energy_N_particles_Product_result.png
Slater determinant - First the normalization overlap - it evaluates to one
out of the N! x N! terms, only N! "diagonal" terms are non-zero
i.e. only the same product from left and right

A21_Normalization_Overlap.png
For single-particle operators - very similar to the overlap
out of the N! x N! terms, only N! "diagonal" terms are non-zero
i.e. only the same product from left and right

A23_Single_particle_operators.png
In the following we illustrate the complexity - but finally we shall see that the evaluation
is in fact quite simple - due to the similarity with the overlap
First helium - NOTE THE APPEARANCE OF THE EXCHANGE TERM

A25_Helium_energy.png
second - Lithium case - three pair terms - at the bottom the Slater determinant
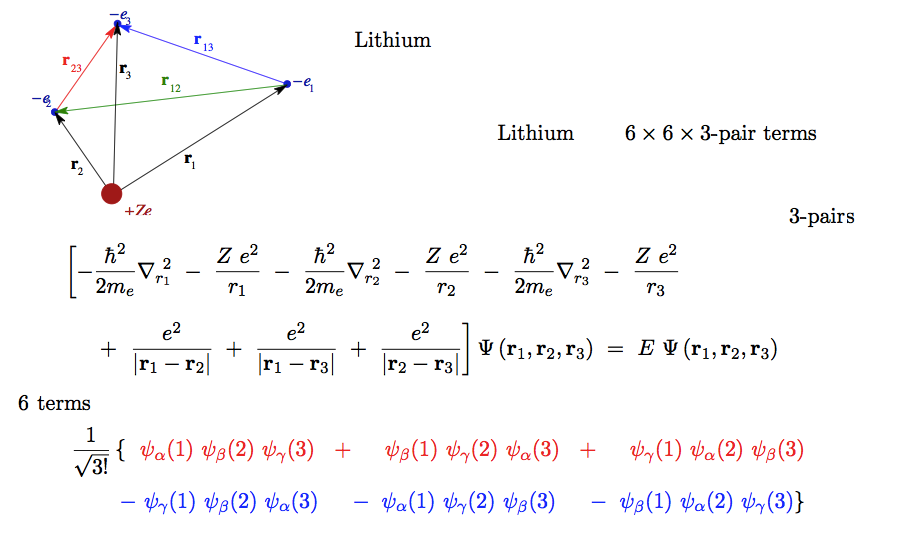
A30_lithium.png
We explore the pair operator situation here: above the red terms have + sign, the blue have - sign
The same notation below - but with rounded rectangle symbols
... we take the first red term against all 6 terms - and one of the pairs r 2-3
it is illustrated that of the 6 terms most are zero
only a direct term (the same on both sides <bc| |bc> ) and one exchanged term 2-3 to 3-2 i.e. <bc| |cb> )
will be non-zero
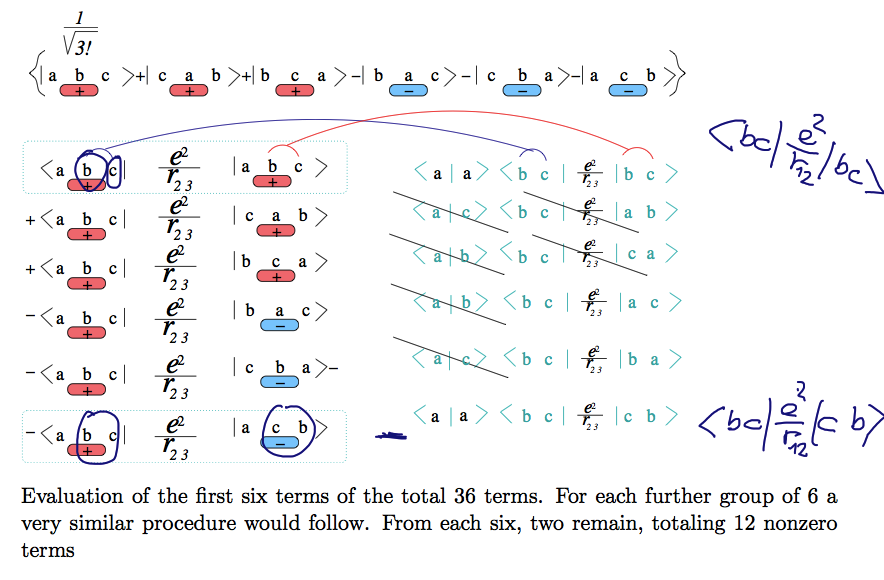
A40_Lithium_pair_terms.png
Final resolution of the pair terms:
It is analogous to the single particle operators - but with addition of the EXCHANGE TERM - see the lithium above
One can simply say:
There are N! terms on each side of the operator
Generally, all those which are not coupled must be the same on both sides (orthogonality)
Thus only the SAME PAIR on both sides of the operator
As seen in the Lithium example - the pair can be swapped
Thus for each PRODUCT term and for each coordinate pair - there is only
one direct term and one exchange term
thus each product has a sum over all orbital pairs
This situation appears N! terms (identically, sum over all orbital pairs)

A50_Slater_pair_terms.png
The single particle operators discussed above
Now the pair - operators - there is the exchange term in addition

A55_Slater_Total_Energy.png
The above is the final result for total energy - including the additional exchange term, as in He
This will be the starting point for the variational approach
Below: Schr. Eq. from variational principle??
The formal derivation is shown

B010_Schroedinger_from_Variations.png
Reminder: Variational methods in clssical mechanics - Minimizing the Lagrange function
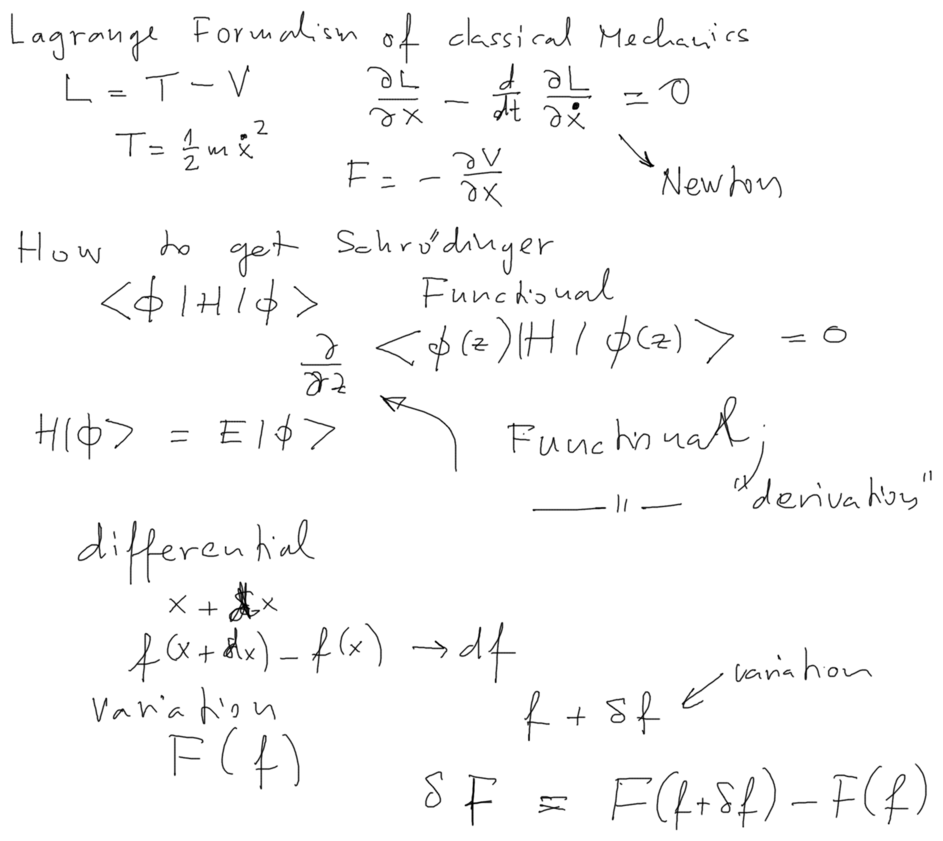
B050_Functionals_Classical_Mechanics.png
NEXT LECTURE: variational derivation of self-consistent field based on the two previous slides:
Schrödinger eq. from variational method
applied to the
Expectation value of total H in the Slater determinant
Such variational method gives N Schrödinger - like equations for N orbitals