Most focus in Quantum Mechanics courses is on the origin of discrete energy levels - and thus the stationary states.
Schrödinger equation is introduced usually in time dependent form, even with possibility of time-dependent total
energy (hamiltonian operator explicitely time dependent)
but then all this is quickly limited to time-independent hamiltonians which can then lead to stationary states.
Mathematically - this is shown by the possibility of sepeartion of time and space coordinates.
Next step is then often the postulate that "only eigenstates are possible outcomes of measurement", and only in
more advanced or complete courses we see some treatment of
- time-dependent perturbation theory
- Fermi Golden Rule - for decay rate of excited systems
- Ramsey or Rabi oscillations
In this part of our course we thus first visit some simple systems, look at the time-dependent Schrödinger equation,
derive "Fermi Golden Rule" - for decay rate of excited systems, but concentrate specially on the natural line widths.
(this and next lecture)
In many texts (even in scientific literature) the existence of natural line widths is ascribed to
"time-energy Heisenberg uncertainety relation",
and the Dirac delta function in the "Fermi Golden Rule" as a "proof" of energy conservation.
We shall see how seriously you should take such statements and those textbooks (hint: not much).
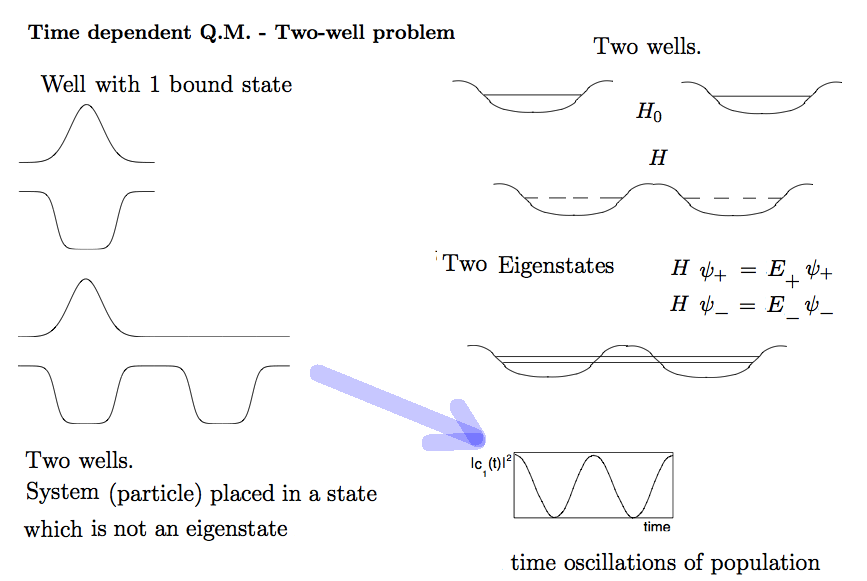
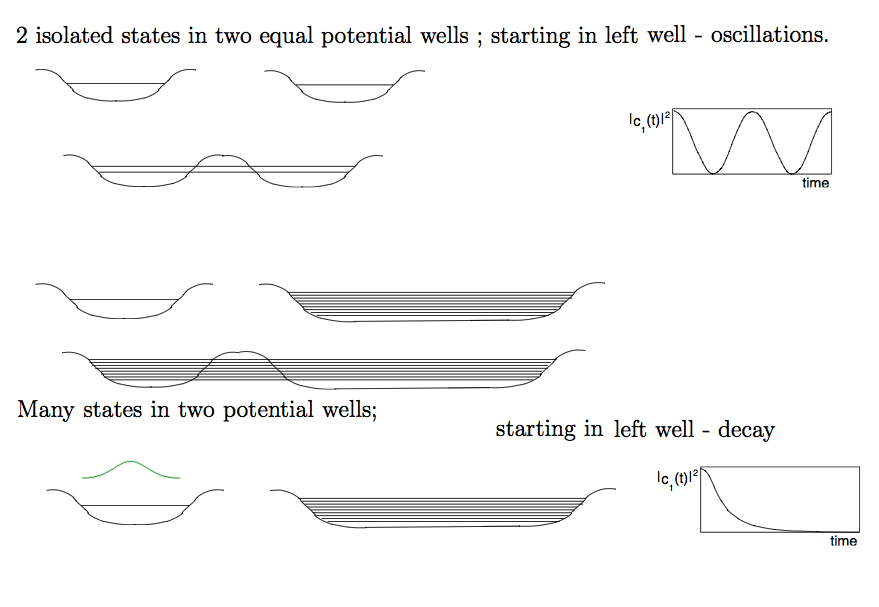
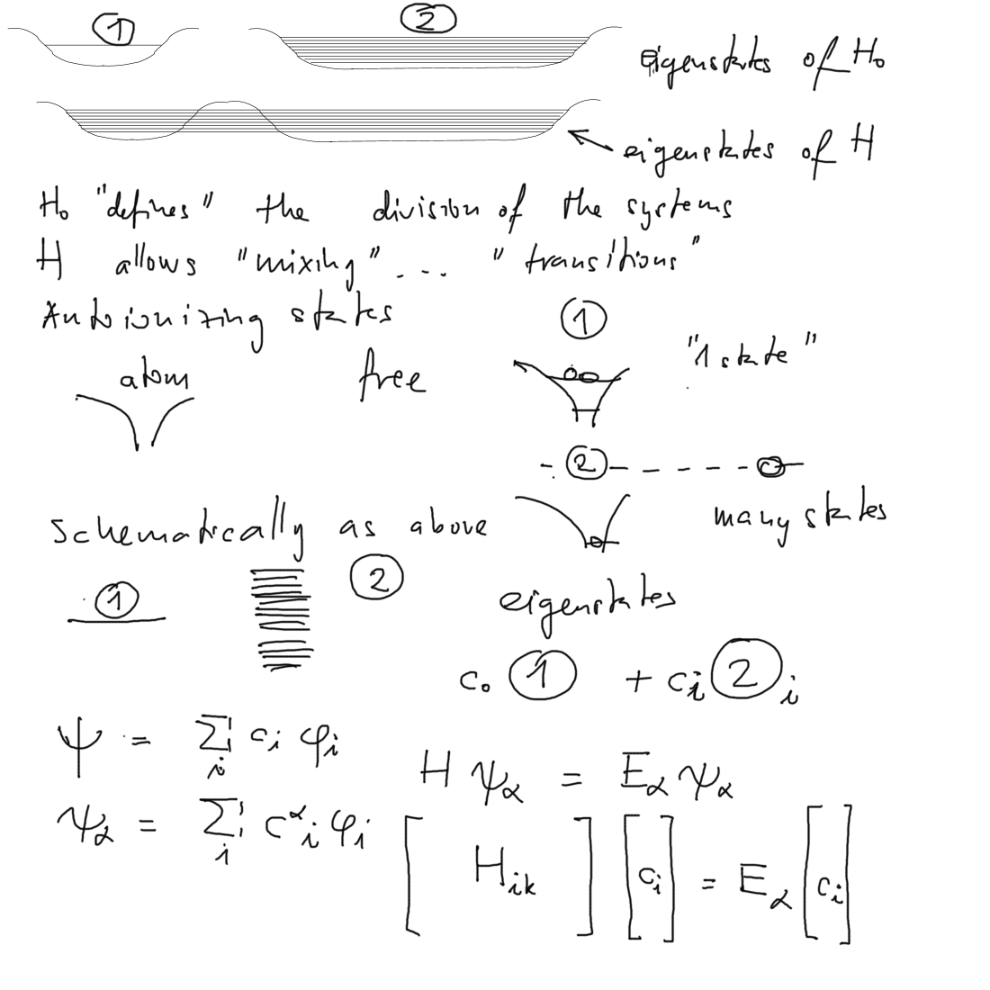
We shall start by time developement in a two-state problem - (well known from some courses)
TWO identical potential wells "competing" to keep bound one particle (think it to be an electron)
Instead of the pictures hamiltonian - for 2 levels H = H0 + V1 + V2
Then we continue by a simple treatment of a general time-dependent total hamiltonian
in a form often used to introduce time-dependent perturbation theory.
WARNING since the captured text is from different parts - the notation is not always consistent
one of the confused notations: sometimes H = H0 + H' and sometimes H = H0 + H1
thus H' and H1 denote both "the extra" coupling energy term
another problem is the notation for the "initial state", sometimes index a, sometimes 0 or even 1
In all cases the meaning should be clear from the context
Two identical potential wells - for simplicity assume that only the chosen potential can "keep" only one bound state.
When these are brought together, i.e. for example one electron bound in two closely placed attracting potential wells,
this system gets two close lying energy eigenstates.
If we drop electron (prepare the system) in one well, we shall get probability density oscillating with time
z_0010_two_wells_system_vs_2_single_wells.png
Well known result illustrated by animation
 |
 This animation shows time developement of PROBABILITY DENSITY |
We know that eigenstates of the whole H = H0 + V1 + V2 form a sort of split doublet (if the wells are moderately separated)
More details are below
Physics: the "electron" is placed in a state at t=0 confined to ONE WELL ONLY (1 well eigenstate)
The probability is seen to be OSCILLATING between the two wells
This is seen from the EIGENSTATES of the whole problem
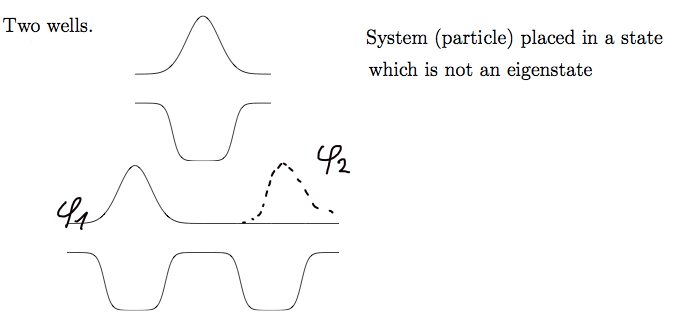
Note that we discuss two "sets" of state, the phi - eigenstates of simplified system, and the psi eigenstates of the whole
system

z_0020_two_well_eigenfunctions_vs_2_single_wells.png
Here we discuss in several rounds the following:
We can expand any state i the particular domain of wavefunctions according to many different basis sets
For us is this of interest:
1. Eigenstates of a simplified system
2. Eigenstates of a "full" system (see the formal definitions below) here
or with an illustration here
The matrix S we mention in the next plate is actually the matrix of eigenstates - see the matlab demo below

z_0023_NOTES-on-two_well_eigenfunctions_vs_2_single_wells.png
The mathematics and an explanation of the animation

z_0030_two_wells_time_developement_superposition.png
In next two plates we illustrate the psi and phi, and their mutual transformations;
Then we show how we can obtain the time developement in two ways
1. solve the Schrödinger equation - time dependent using expansion in the phi-set
2. use the fact that the solutions of the "total problem" have "independent" time-dependent solution (the exponential energy-phase)
and expand each of the psi in terms of phi - where one of the phi-set is the initial condition
(electron in the left well; see next plate; here general formulae)

z_0050_eigenstates_of_H_vs_H_0__expansions.png
The yellow-plate below is a copy of the above one - but with added psi and phi of the TWO WELL PROBLEM (white spots)

z_0055_eigenstates_of_H_vs_H_0__expansions_TWO-WELL.png
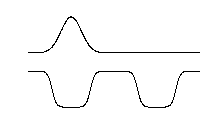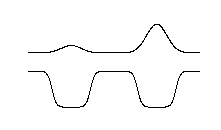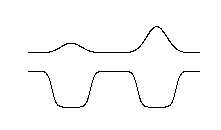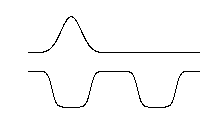
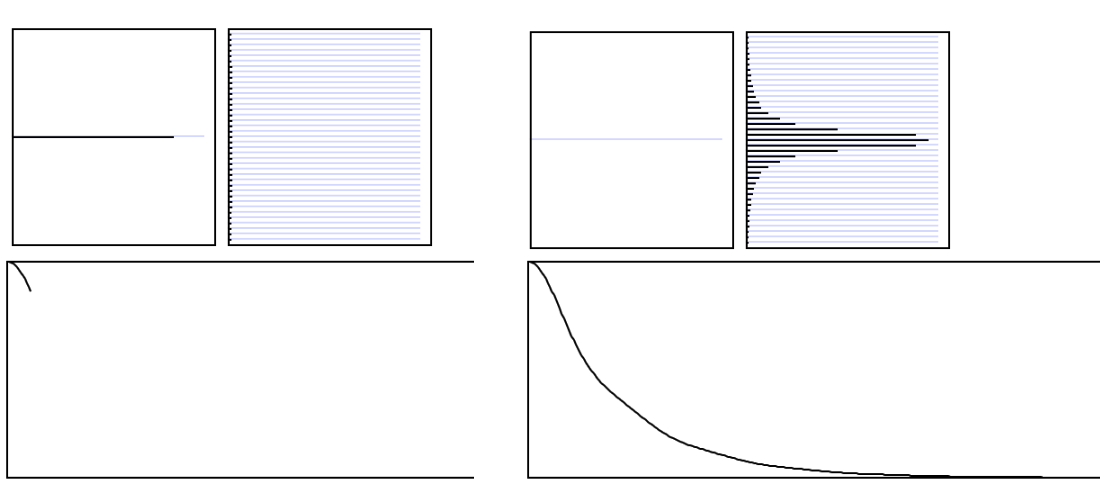
Now we turn to different two wells: (upper part: already discussed oscillating probability)
- in the lower part: shown are the many eigenstates - quasicontinuum
- and the result - for really many states, quasicontinuum, we will observe a decay of the original density
z_0100_2_wells_with_quasi-continuum-decay_not_oscillation.png
Animations; the two well illustration

two equal wells oscillations two wells - one well with quasicontinuum - decaying population
Below: The same slide as the above - but this is the original - with notes from the lecture

z_0105_2_wells_with_quasi-continuum-decay_not_oscillation.png
Two wells: one with many eigenstates - quasicontinuum
and the result - for really many states, quasicontinuum, we will observe a decay of the initial probability density
also
another illustration of the important aspect of "two sets of eigenstates" - those of H0 and those of H = H0 + H' (or H = H0 + H1 )
z_0110_2_wells_with_quasi-continuum-qutoioniz_example.png
Reminder - how do find the eigenstates; expansion in eigenstates of "simpler" system
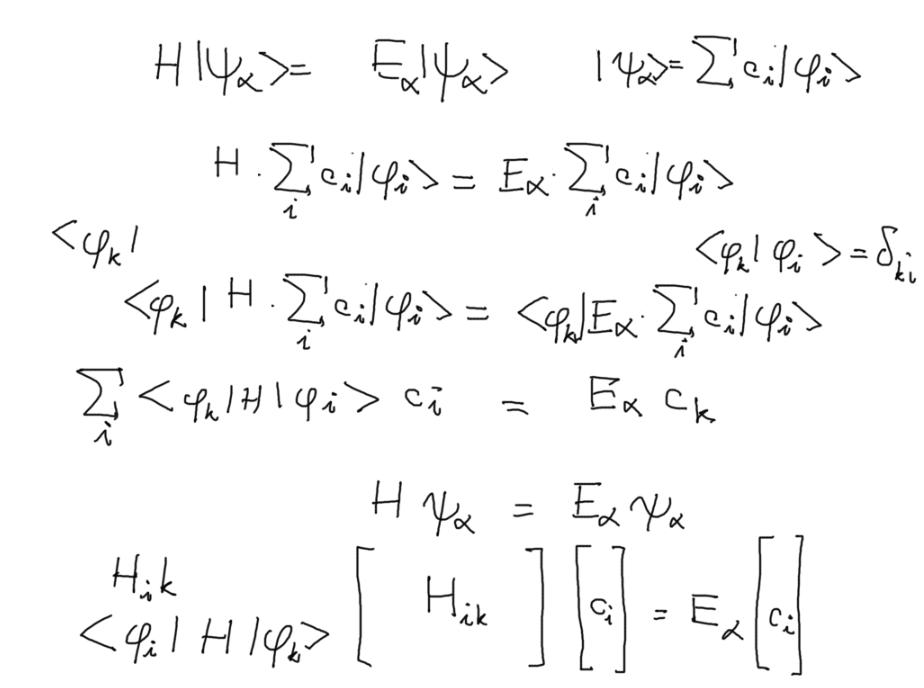
z_0120_finding_eigenstates_expansion.png
Two wells: one with many eigenstates - quasicontinuum
and
Energies in a matrix version of the model
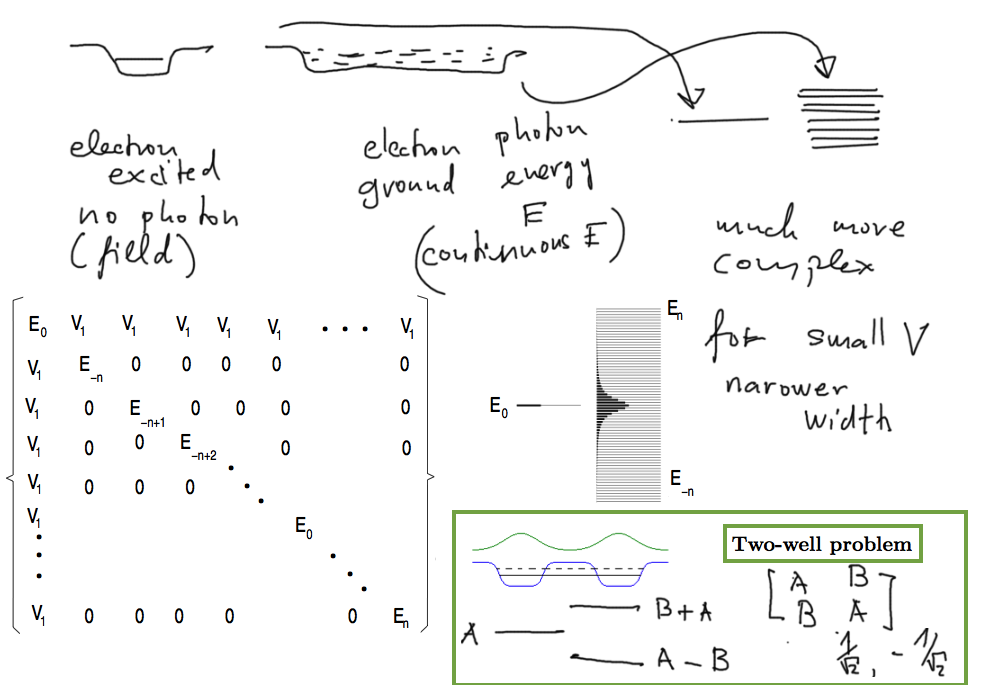
z_0150_finding_eigenstates_expansion.png
Snapshots from folk.uib.no/nfylk/PHYSTOYS/golden/
This webpage is a javascript program solving the TDSE (each new parameter set takes a few secs)
( try the N=2, N=4, .... N=20 clicks )
z_0200_solving_time-dep-Schrodinger.png
The Fermi golden rule simulator illustrated

z_0220_Golden_Rule_Simulator_solving_time-dep-Schrodinger.png
Finding eigenvalues in matlab - a very small matrix of the above H ( N=8) type

z_0230_Matlab_H_Eigenvalues.png
The above examples should have shown the situation when the system is "forced" to start from a state which is an eigenstate
of a "simplified system (e.g. only one well - or better two completely isolated levels without penetration possibility)
BUT NOT an EIGENSTATE of the total system - Then we can have a decay
In the next part we recorded the solution of time dependent Schrödinger equation using an APPROXIMATION
Time dependent perturbation theory

z_0500_Time_dep_Schroedinger.png
Time - dependent Schrödinger equation - expansion in phi - before applying Time dependent perturbation theory

z_0510_Time_dep_Schroedinger-MATRIX_FORM.png
Time dependent perturbation theory

z_0520_Time_dep_Perturbation_Theory.png
Time dependent perturbation theory
assumptions: The change is small, the original expansion coefficient remains close to one ( = 1 )

z_0530_Perturbation_Theory_assumptions.png
Time dependent perturbation theory Eliminating the time exponential phase factor
only "the coupling" hamiltonian remains

z_0540_Matrix_to_Column_decouple_equations.png
Time dependent perturbation theory Decoupling of the coupled equations - see above

z_0550_Perturbation_decouple_equations.png
Time dependent perturbation theory the decoupled equations are easily solved

z_0560_Evaluate_time_integrals_perturbation.png
Time dependent perturbation theory - rearranging the "probability expression" - as function of omega times time
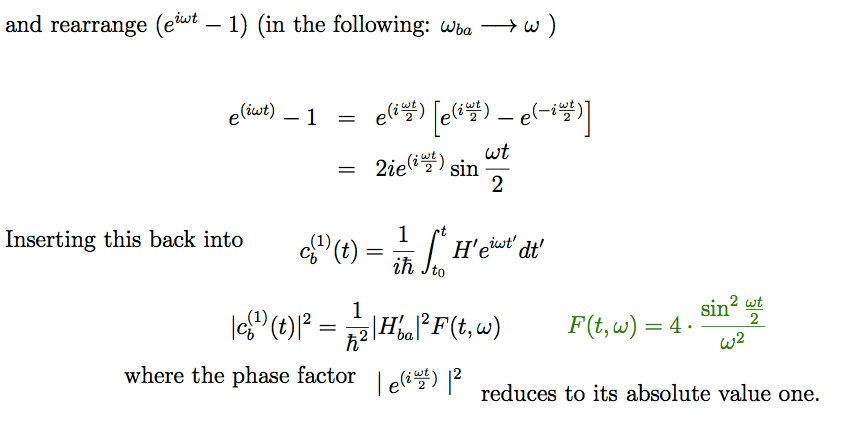
z_0580_Evaluate_time_integrals.png
Time dependent perturbation theory the rearranged "probability" will look like a delta function of omega for large t
see below

z_0600_Dirac_delta_origin.png
Time dependent perturbation theory the rearranged "probability" as a function of x = omega t
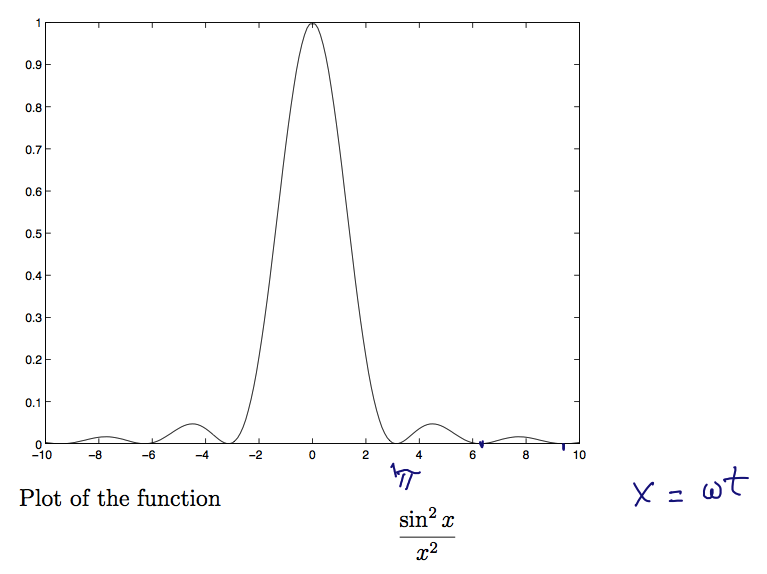
z_0610_Dirac_delta_Sine_step.png
Time dependent perturbation theory the rearranged "probability" looks like a delta function of omega for large t
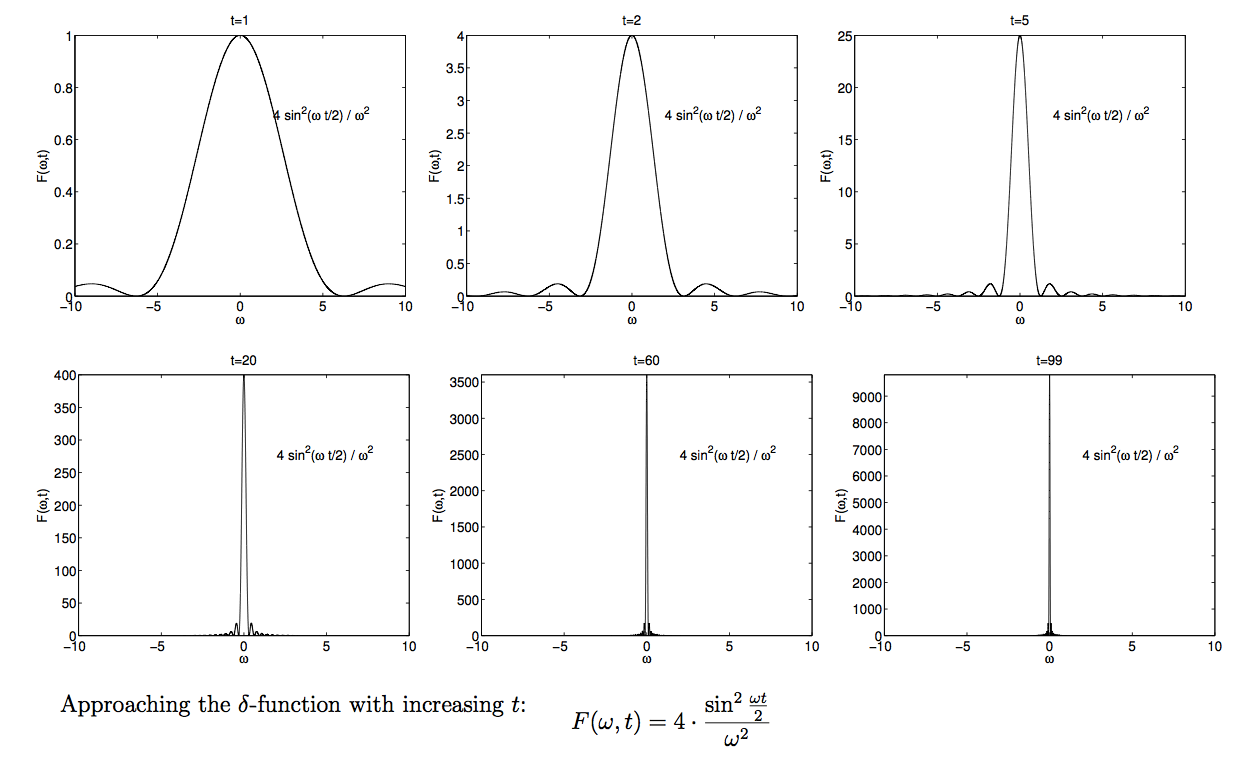
z_0620_Dirac_delta_Approaching.png
Time dependent perturbation theory summing the probabilities over "all the relevant final states - integral in continuum limit

z_0650_Probability_of_change.png
Time dependent perturbation theory summing the probabilities over "all the relevant final states - integral in continuum limit
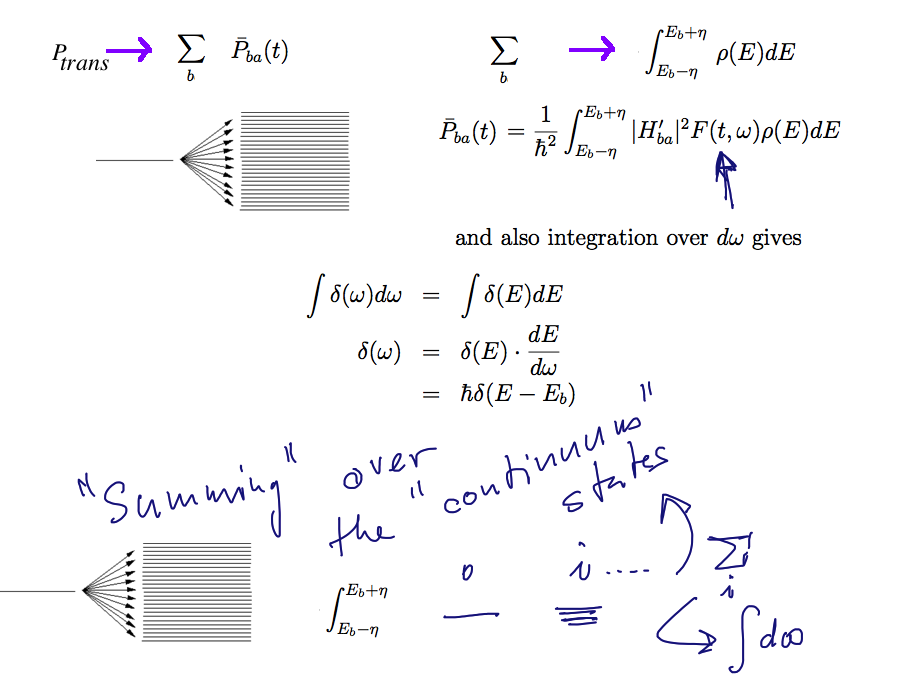
z_0680_Summing_Probability_of_change--Fermi_Golden.png
Time dependent perturbation theory summing the probabilities over "all the relevant final states - integral in continuum limit
Fermi Golden rule

z_0700_Fermi_Golden_Rule.png
Fermi Golden rule: constant rate of probability change from Perturbation theory (note that the delta function disappears)
The density of states appeared when we replaced the summation by an integral
This is always so: summation ---> integral allways needs "density of states"
( see also density of states in the NEXT LECTURE )
NEXT LECTURE: Exponential decay from constant rate. Natural line width and further details of the electromagnetic field