to index              2015_11_18 Previous lecture note             LECTURE NOTE    2015_11_19           2015_11_25 Next lecture note

Light -Atom Interaction - Part 2
Exponential Decay, Line Width, Eigenmodes of Vibrations


In this lecture   
                       1. Exponential decay from constant rate
                       2. Natural line width
                       3. Density of states   -  for light waes ( photons )
                       4. Eigenmodes of harmonic systems  (coupled oscillations)

 1. Exponential decay from constant rate    we must modify the constant rate - depends also on "how much is left" 

      1000_Constant_RATE-decay.png

       1000_Constant_RATE-decay.png
 

Exponential decay from constant rate         and             Natural line width   part 1 - from the  exponential decay result
      1010_Exponential_Decay_Line_width.png

       1010_Exponential_Decay_Line_width.png
                      
    The assumption of perturbation theory can not be kept (   c0  = 1 must be replaced by square root of probability - look above )
     Exponential decay from constant rate         ----->               Natural line width
                       
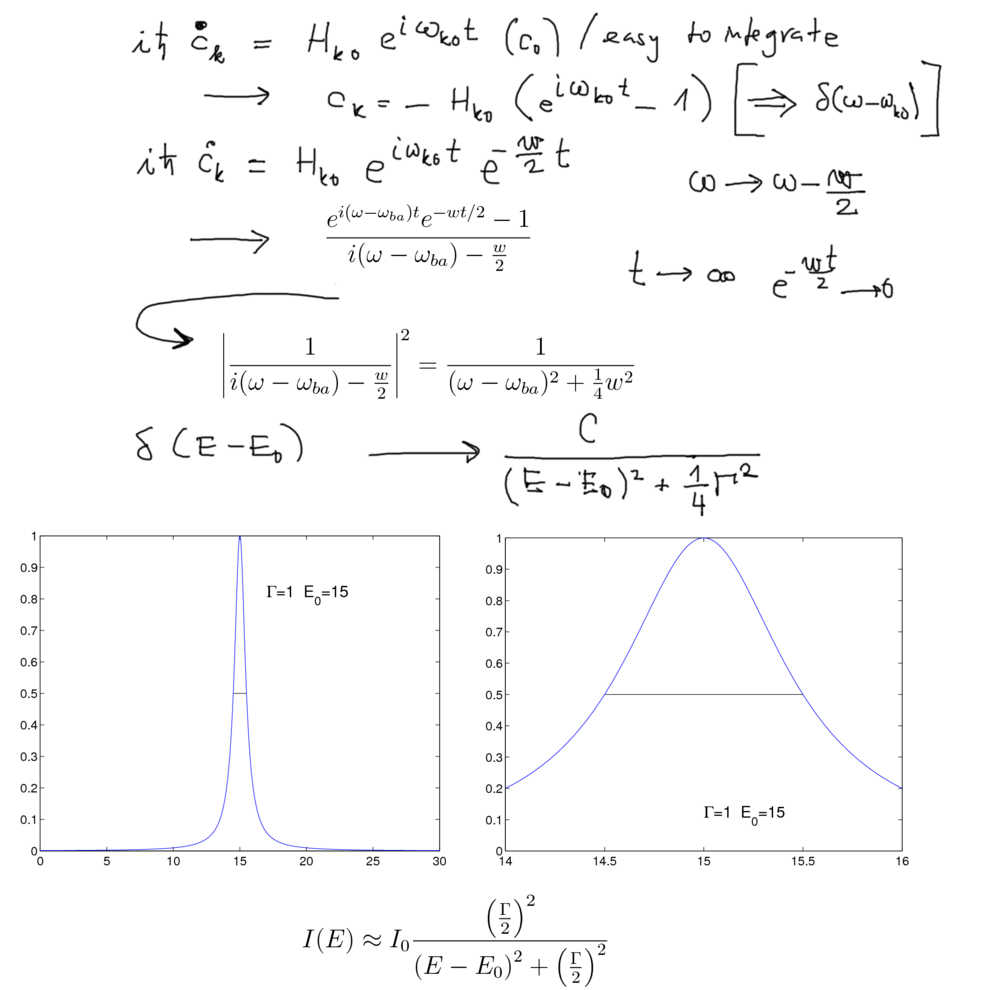
      1020_Line_Width_replaces_Dirac_Delta.png

       1020_Line_Width_replaces_Dirac_Delta.png
      The curve (spectral line) shape above is called Lorentzian shape;
      as opposed to random background phenomena -  Gaussian shape    ( G(E, E0) =)   exp(- (E - E0)^2 / Delta^2  )
 
              Natural line width   (Lorentz shape)
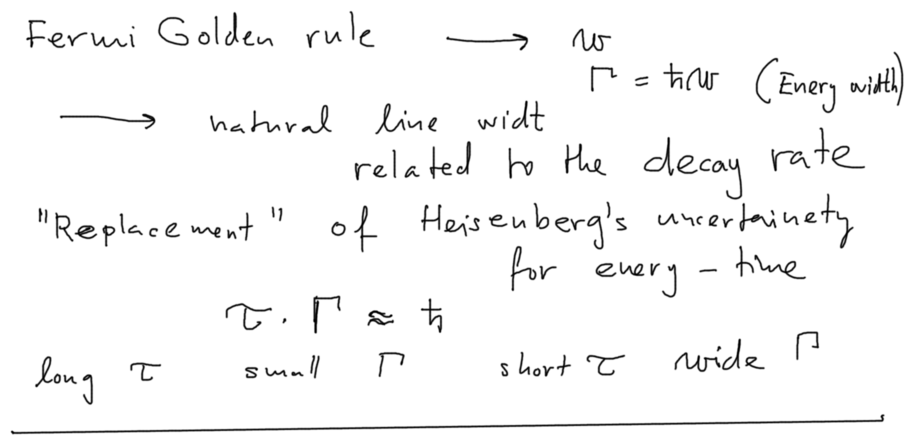
      1030-Summary-Line_Width_NO_Dirac.png

       1030-Summary-Line_Width_NO_Dirac.png
   
    Density of states   -  for light waves ( photons )      -     Discretization by periodic boundary conditions
                     
    The density of states appears whenever we replace a summation by an integral
                                                                                       This is always so:     summation ---> integral     allways needs "density of states"
                                                                                                                              (also in the Golden Rule derivation last time)
                                                                                       Dimensional argument
      1100_Density_of_states.png

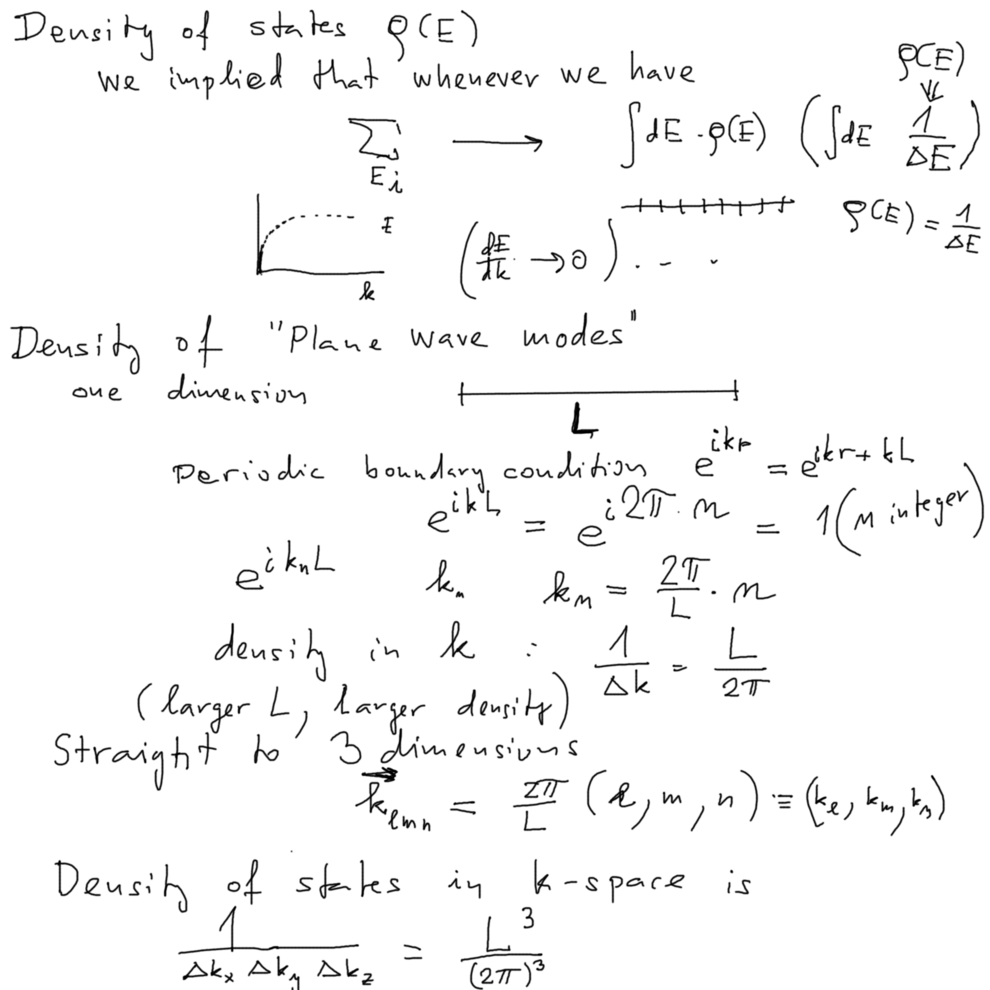
       1100_Density_of_states.png
   
    Density of states   -  for light waes ( photons )   Discretization by periodic boundary conditions
              
      1120_Density_in_K-space_to-Energy.png

       1120_Density_in_K-space_to-Energy.png
   
  Eigenmodes of harmonic systems  (coupled oscillations)
 
          Formal transformation of the total energy
   
      1140_Eigenmodes_Coupled_Harmonic_oscillations.png

       1140_Eigenmodes_Coupled_Harmonic_oscillations.png

   
  Eigenmodes of harmonic systems  (coupled oscillations)
 
          Formal transformation of the total energy
   

      1150_Eigenmodes_via_transformations.png

       1150_Eigenmodes_via_transformations.png
   
  Eigenmodes of harmonic systems  (coupled oscillations)
 
          Formal transformation of the total energy
   
      1160_Eigenmodes_via_transformations.png

       1160_Eigenmodes_via_transformations.png

   
  Eigenmodes of harmonic systems  (coupled oscillations)
 
          Formal transformation of the total energy
   
      1170_Eigenmodes_via_transformations.png

       1170_Eigenmodes_via_transformations.png

     Example: N balls connected by springs - coupled oscillations
      1180_Eigenmodes_N-balls-example.png

       1180_Eigenmodes_N-balls-example.png

      Example: N balls connected by springs - coupled oscillations
      1190_Eigenmodes_N-balls-example_Matrix.png

       1190_Eigenmodes_N-balls-example_Matrix.png

  Finding the eigenmodes - means expressing the system energy (hamiltonian)
                                            as a system of independent harmonic oscillators
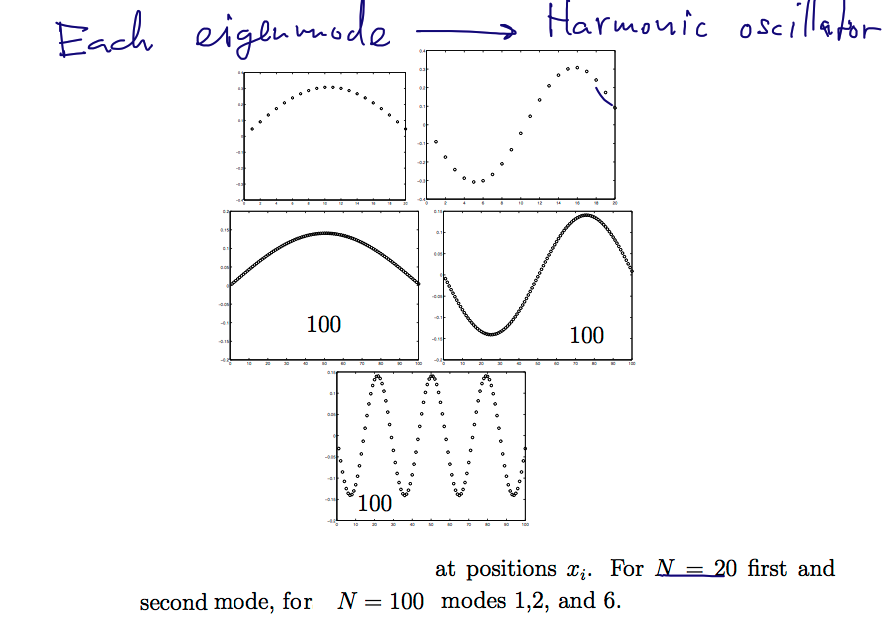
      1195_Eigenmodes_N-balls-example_amplitudes.png

       1195_Eigenmodes_N-balls-example_amplitudes.png

  Finding the eigenmodes - means expressing the system energy (hamiltonian)
                                            as a system of independent harmonic oscillators
      1200_Eigenmodes_summary_Harmonic_oscillator.png

       1200_Eigenmodes_summary_Harmonic_oscillator.png

Algebraic method for the Harmonic oscillator - Creation and annihilation of "energy quanta"

The following three slides were just previewed; This will be detailed NEXT TIME
      1220_Harmonic_Oscillator_Creation_Annihilation.png

       1220_Harmonic_Oscillator_Creation_Annihilation.png

Algebraic method for the Harmonic oscillator - Creation and annihilation of "energy quanta"
Here just previewed; This will be detailed NEXT TIME
      1230_Harmonic_Oscillator_Creation_Annihilation.png

       1230_Harmonic_Oscillator_Creation_Annihilation.png
 
  Algebraic method for the Harmonic oscillator - Creation and annihilation of "energy quanta"
  Only previewed; This will be detailed NEXT TIME
      1250_Harmonic_Oscillator_Creation_Annihilation.png

       1250_Harmonic_Oscillator_Creation_Annihilation.png

Algebraic method for the Harmonic oscillator - Creation and annihilation of "energy quanta"
The last three slides will be detailed NEXT TIME

to index              2015_11_18 Previous lecture note             LECTURE NOTE    2015_11_19           2015_11_25 Next lecture note