In this part:
1. Algebraic method for harmonic oscillator - creation and annihilation operators a+ and a
this is needed to treat each of the eigenmodes ( each one is an independent oscillator )
2. Quantum theory of the electromagnetic field - two expressions for energy of the field
in eigenmodes, using a+ and a and using the derived operators for electric and magnetic field strengths
3. From Lorentz Force to hamiltonian of charged particle in electric - and magnetc - field ATOM-FIELD INTERACTION
4. Applying the golden rule - what will be the matrix elements
Algebraic method for the Harmonic oscillator - Creation and annihilation of "energy quanta"
The next three (smaller size slides) were shown at the end of LAST TIME
the hamiltonian is transformed to simple and symmetric, dimensionless-operator based form
Linear combination of this dimensionless coordinate Q and momentum P - leads to annihilation / creation operators

1220_Harmonic_Oscillator_Creation_Annihilation.png
Algebraic method for the Harmonic oscillator - Creation and annihilation of "energy quanta"
Linear combination of this dimensionless coordinate Q and momentum P - leads to annihilation / creation operators
ONLY USING commutation relations

1230_Harmonic_Oscillator_Creation_Annihilation.png
Linear combination of this dimensionless coordinate Q and momentum P - leads to annihilation / creation operators
ONLY USING commutation relations
Hamiltonian Number operator eigenstates characterized by "number of quanta"

1250_Harmonic_Oscillator_Creation_Annihilation.png
Linear combination of this dimensionless coordinate Q and momentum P - leads to annihilation / creation operators
ONLY USING commutation relations
creation and annihilation operators a+ and a
Hamiltonian Number operator eigenstates characterized by "number of quanta"

005_creations_commutations.png
Ladder operators creation and annihilation operators a+ and a

006_Quanta_Number__LADDER_operator.png
Looking back at the wavefunction formulation operators a+ and a are in fact partly differentiation ......
Schrödinger equation - replaced by effective first order differential equation

007_differential_eq-via_Ladder_operator.png
Quantum theory of the electromagnetic field
- two expressions for energy of the field
in eigenmodes, using a+ and a and using the derived operators for electric and magnetic field strengths
Establishing the dimensional constant ( from the equality of the two energies )

008_Quantum_Description_of Field_vector_pot_A.png
Establishing the dimensional constant ( from the equality of the two energies )
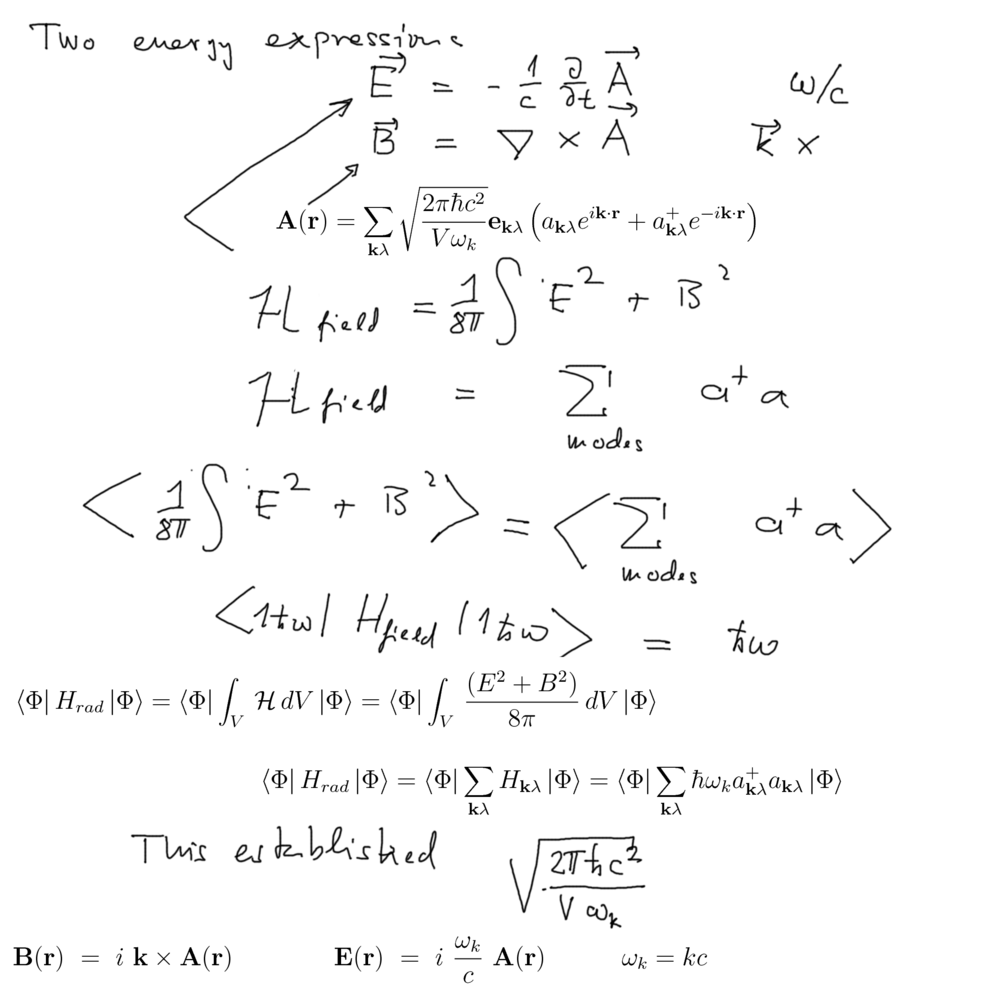
010_Classical_Quantum_total_energy_same_M.E.png
ATOM-FIELD INTERACTION
From Lorentz Force to hamiltonian of charged particle in electric - and magnetc - field

018Charged_Particle_Lorentz_Force.png
ATOM-FIELD INTERACTION
hamiltonian of charged particle in electric - and magnetc - field

019_Field_Atom_Interaction.png
ATOM-FIELD INTERACTION
hamiltonian of charged particle in electric - and magnetc - field
a map of the steps in applying Golden Rule identifying the H0 and H1

020_Hamilton_Field_Atom_Interaction.png
ATOM-FIELD INTERACTION
applying Golden Rule identifying the H0 and H1 initial and final (continuum) states

030_Apply_Golden_Rule_to_Atom_Field.png
Discussing details of the resulting matrix element
what are electronic (red) and what are field (blue) components
the field is quantized, its description is in terms of creation / annihilation expressions
but the "eigenmodes" are in the normal 3-dim space - so they will be the same as the electron coordinates
( the exp(- i k r ) - r is the same coordinate as the electron )

060_Matrix_Element.png
Note above the sign in the exponentials - ( discussed also in the next lecture )
now changed in agreement with literature - but is seemingly opposite to our usual conventions for plane waves
In the NEXT LECTURE we carry through the details of the light emission rates
and discuss the stimulated emission in this framework