In this part
1. we evaluate the details of the light emission rates
2. discuss the stimulated emission
3. shortly mention the laser
4. shortly discuss the physics of molecules - and their spectra
The notation here should be now clear: Golden Rule, Probability change rate W, density of states
The interaction HI has been discussed - comes basicaly from the Lorentz Force

010_Golden_Rule.png
The momentum operator p is the momentum of the electron; A is the operator of the "vector potential" of the field
And thus expressed using the mode's creation, anihilation operators
Note that we must be summing over "all the modes"; e the polarization vector
Initial and final states are mentioned - here generally - see below for a more specific discussion
Note that there is also a definition of the "transition frequency" in terms of energies

020_Golden_Rule_Applied.png
Next slide - everything is inserted - the constant expressing the field dimensions (square root....), density of states etc

030_Golden_Rule_Applied_details.png
Here are the details of the matrix element evaluation
what are electronic (red) and what are field (blue) components
As mentioned before, the field is quantized, its description is in terms of creation/anihilation expressions
but the "eigenmodes" are in the normal 3-dim space - so they will be the same as the electron coordinates
( the exp(i k r ) - r is the same coordinate as the electron )
Also note the problem exp(i k r - i omega t ) and exp( - i k r + i omega t ) - seems to be
inconsistent conventions - we do not have the solution yet

040_Matrix_Element_details.png
Further simplifications - so called Dipole approximation
first - long wavelength approximation, get rid of the exponential exp ( i k r )
then transform the p-operator matrix element to the matrix element of r - that makes the dipole

050_dipole_approximation.png
More on Dipole approximation
transforming the p-operator matrix element to the matrix element of r - that makes the dipole
using the commutation relation [ r, H ]

060_dipole_approximation.png
Working with the "density of states " when discussing that - we left the integration over the directions open
now we shall perform the integration over directions
This is somewhat too detailed, discussed only for completeness
This is done in a clever way: the < b | p | a > is a given vector (three numers, while vector p is 3 operators )
Thus this vector is chosen as a definition of the z-axis, very clever!
Mentioned at the end of this slide, used in next slide

070_evaluation_details_emission_angle.png
Working with the "density of states " - performing the integration over directions
( This is somewhat too detailed, discussed only for completeness )
This is done in a clever way: the < b | p | a > = P' is a given vector (three numers, while vector p is 3 operators )
Thus this vector is chosen as a definition of the z-axis, very clever!
This also includes summation over the polarizations - even more clever trick - with this choice of axes
only one polarization ( but in "real space" no such exclusion! )
( look at the rounded frames ..... the 0 scalar product)
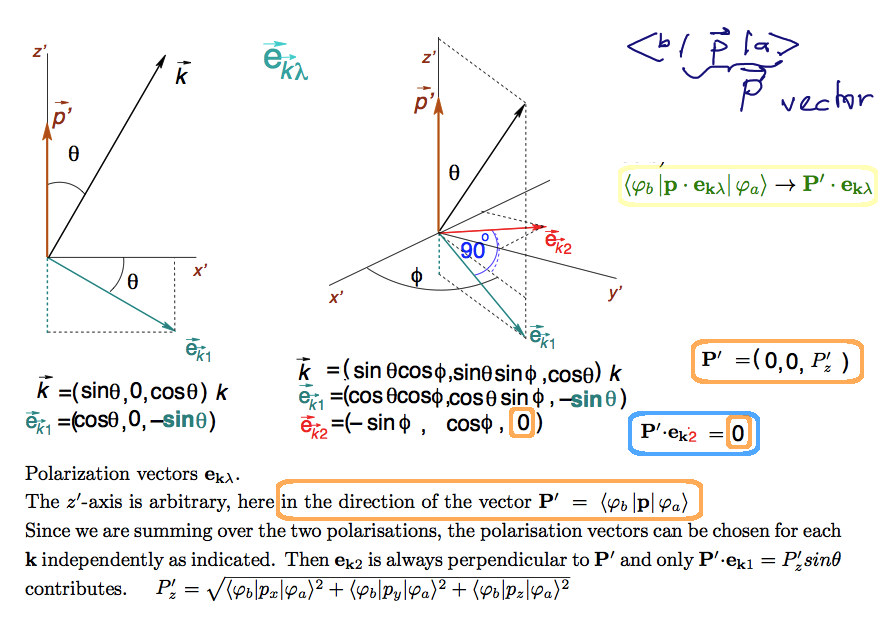
080_evaluation_details_emission_angle.png
Now this is combined into the expressions from before, look at the simple integral giving the 8 pi/3 result

090_evaluation_details_emission_angle.png

100_Final_result_Physics_dimensions.png
Understanding stimulated emission in the language of creation/anihilation operators
This is really one of the nicest results here

110_stimulated_emission.png
The story of the LASER - a popular presentation - this explains "Population Inversion"

180_population_inversion.png
The laser light is ( ideally ) much more a "classical wave" than "stream of photons"
Nobel prize winner Roy Glauber ( just turned 90 this november, congratulations! ) explained this
Glauber states http://folk.uib.no/nfylk/PHYSTOYS/glauber/
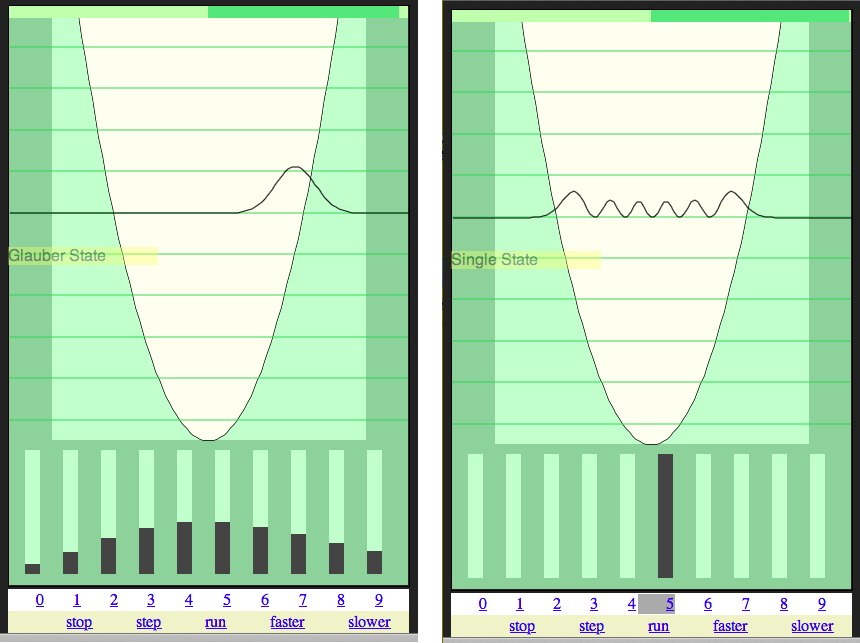
190_coherent_states_H.O.png
The basics of Molecular physics
Why are molecules bound states - electronic states - H2+ example (hydrogen molecule ion )
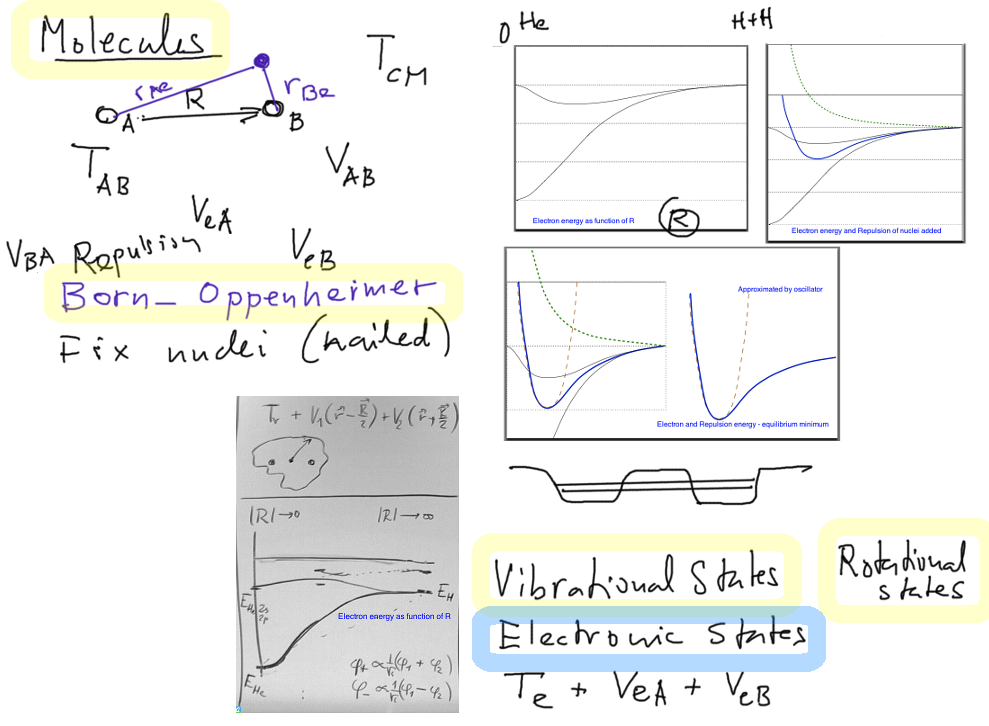
250_Molecular_Binding_Spectra_etc.png
Electronic states in a homonuclear molecule (bothe nuclei the same, homogeneous ... )
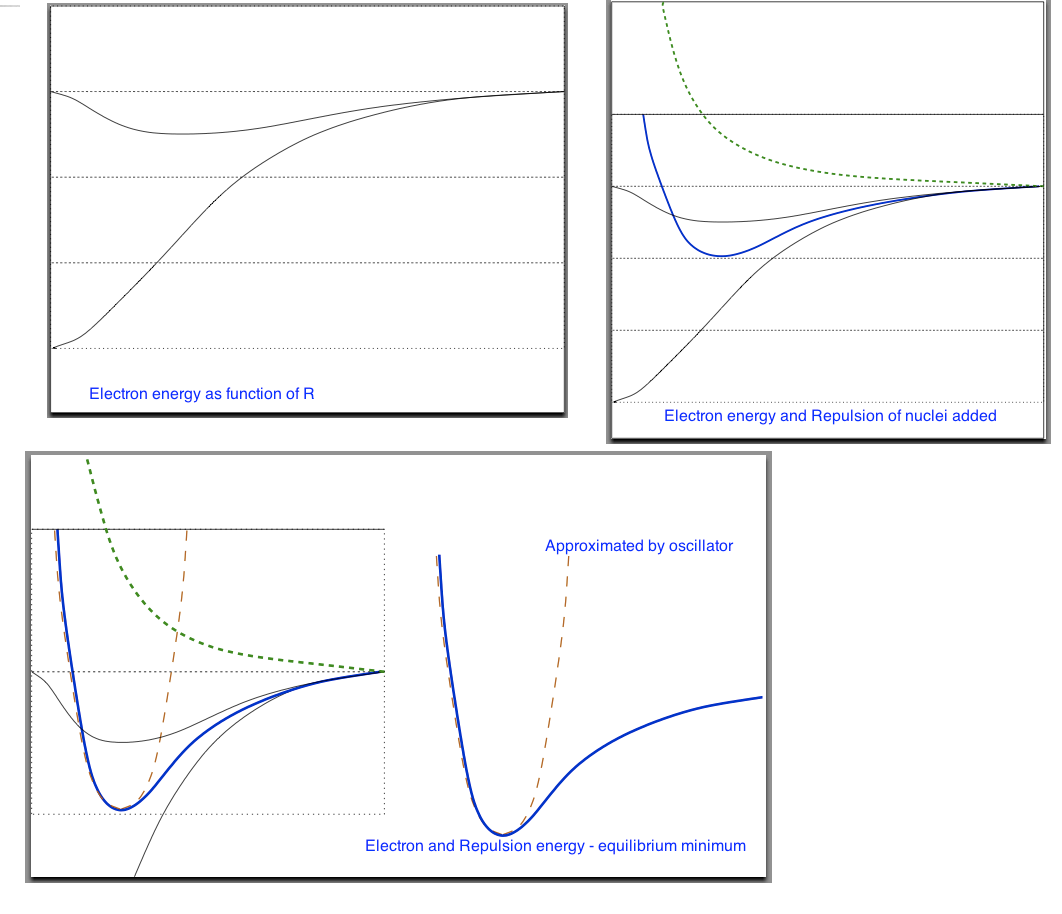
290_molecular_binding.png
Three types of molecular spectra
- electronic states ( ~ eV )
- vibrational states ( ~ 0.01 eV )
- vibrational states ( ~ 0.001 eV )

300_molecular-spectra_elctr_vibr_rot.png
It might be of interest to look at older notes, for example
http://web.ift.uib.no/AMOS/PHYS261/2011_11_10/
where we have listed also even older links
Molecules
http://web.ift.uib.no/AMOS/PHYS261/03.11.12/index0.html
Exotic Atoms
http://web.ift.uib.no/AMOS/PHYS261/2004.11.18/index0.html
2004.10.07 Blackboard shots; Molecular Physics
Pictures of molecular states
2004.10.27 Blackboard shots; Last part Molecular Physics
Lecture: Physics of Molecules
2004.11.17 Short blackboard shots; Effects, Structures Spectra. Dirac equation
2004.11.18 Blackboard shots; Effects, Structures Spectra. Exotic and Hollow Atoms