Many electron atoms - part 3
We started by reviewing the variational approach to Schrödinger "derivation", how to justify that
only one variation of phi appears, and only on "the left side".
The usual argument is that - if formulated with integrals - the Phi and Phi* are two independent
variable functions, so that we must consider variation of both - and we start with the variation of the
Phi* - or in Dirac notation - the < | vector. And that already brings the desired result, we do not
need to continue to the condition for Phi

0010_Variational_derivation.png
Applying the same to variation of many-electron energy
Notation issues:
1. Variation of the whole function - all the occurencies of e.g. alpha must be replaced by its variation
i.e. for all position variables rk - and because of the overlaps-conditions only the terms indicated below
remain nonzero
2. Variation of terms including the two-paricle operators - we do not have a simple notation
< a b | V(1,2) | c d > is the double - integral
< b | V(1,2) | d > - one of the variables, say 2, is not integrated over so that G(1) = < b | V(1,2) | d >
This has been discussed in the following slides

0020_Meaning_of_the_notation.png
< a b | V(1,2) | c d > denotes the double - integral
< b | V(1,2) | d > - one of the variables, say 2, is not integrated over so that G(1) = < b | V(1,2) | d >
perhaps we should use
( b | V(1,2) | d ) - to indicate that it is not the same as the
This has been discussed in detail here in this slide - in the colored part
REMINDER OF THE Hartree - Method - interaction with the charged cloud
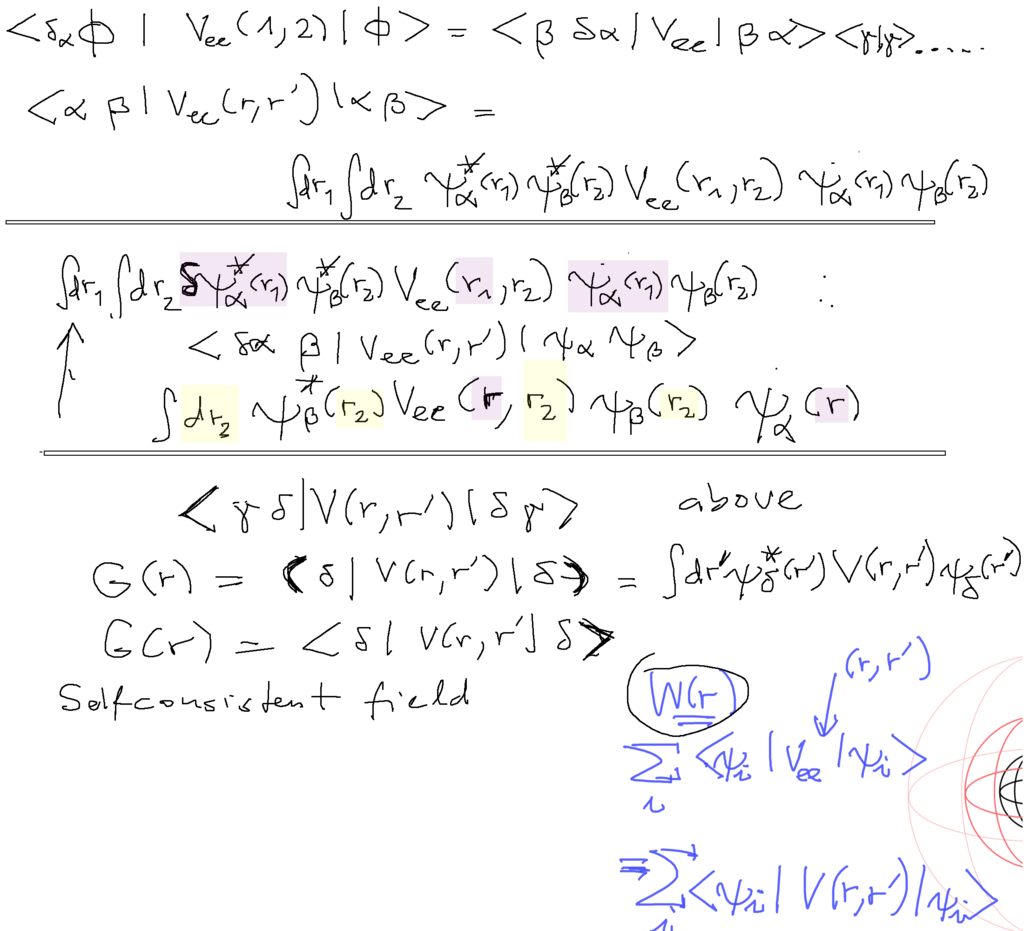
0030_Connection_with_Hartree_method.png
The details of the Hartree-Fock equations - best seen with the notation with integrals
The direct term is simple
The exchange term - note the summation
Non-locality of the exchange term
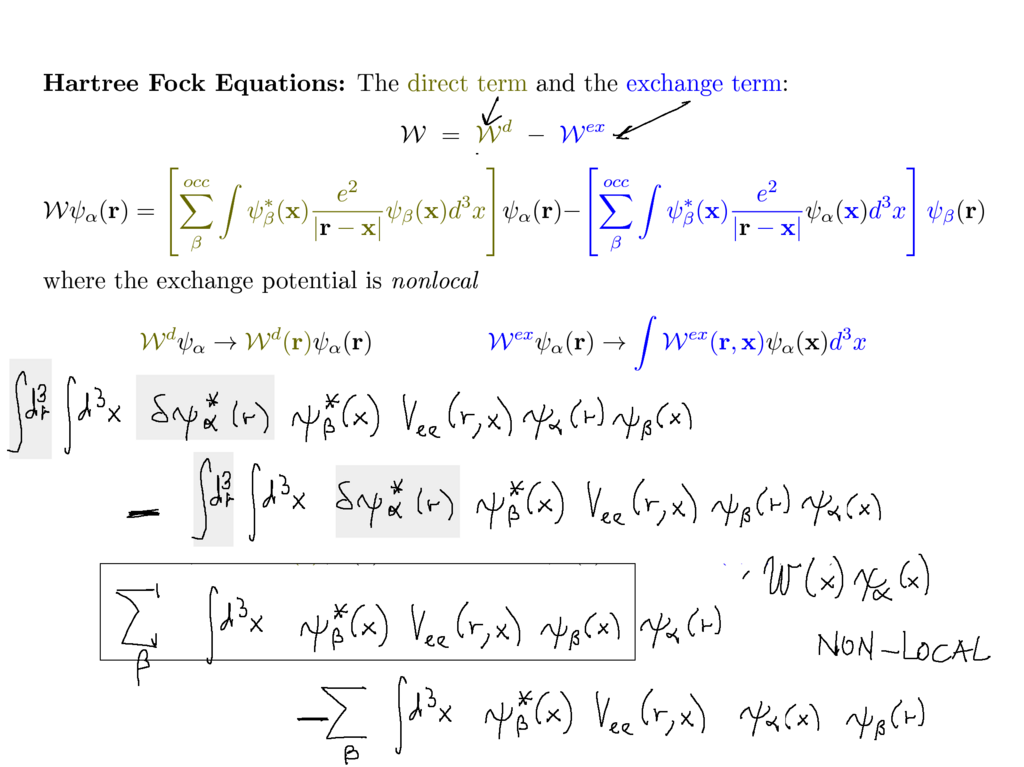
0043_exchange.png
Non-locality of the exchange term
Hand-written part - what is non-local operator
we start with the superposition statement
and show the origin of the unit-operator relation
including the projection operators | a > < a |

0050_Local_nonLocal.png
Unit operator - containing projection operators | a > < a |
Generalized to eigenstates of position integrals - and delta-functions involved
What follows: basically all operators should be non-local;
our favourit multiplication operations, as the discussed potential operation
contain the delta - function
The exchange potential appears by construction non-local
Solution of Hartree- Fock equations - they contain "integro-differential equations" for the orbitals
Usually some further approximations

0060_Local_nonLocal.png
Next time -
(a) DFT - density functional theory
(b) configuration mixing
(c) spectroscopic terms - notation of L S J states (angular momentum, spin, and total J )