Many electron atoms - part 2
Slater determinant - review - see last time - permutations - sum over product functions of the same sequence of coordinates
but with permutation of orbitals (could be vice versa, but this is easier to use in our context - and consistent with Dirac notation )

0000_1_Intro.png
.... more about determinants
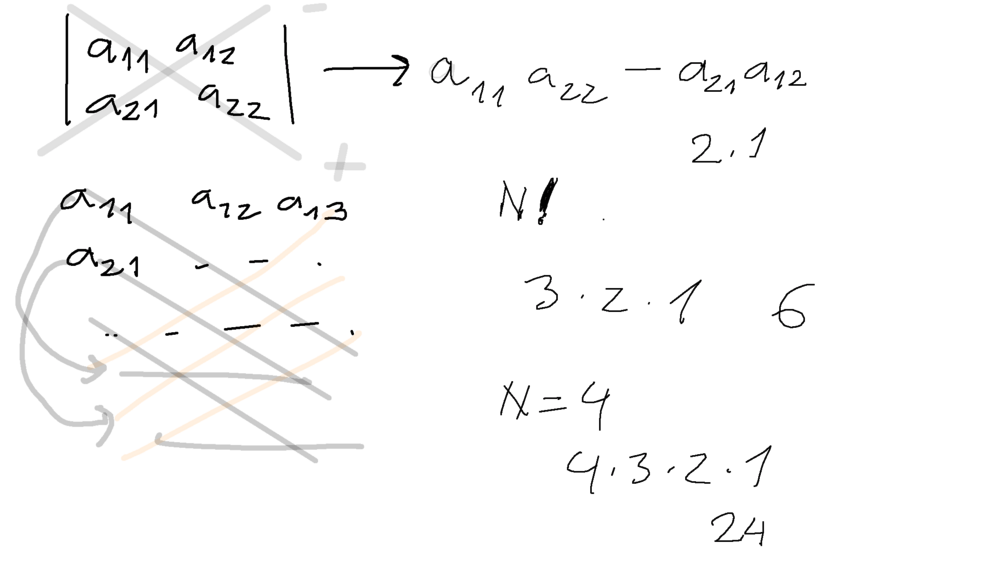
0000_2_determinants.png
Expectation value of energy - first we look at a single product of orbitals
We easily establish that - because there is only one product of orbitals, one term
- but sum over coordinates and sum over pairs of coordinates -
- and to each coordinate belongs one orbital -
that sum over coordinates ( for Hs - single particle operators) --> sum over orbitals
sum over PAIRS of coordinates --> sum over all pairs of orbitals
first the Hs - single particle:

0000_31_Product_Hs.png
... and here sum over PAIRS of coordinates --> sum over all pairs of orbitals
note that if (1,5) appears, there is no additional (5,1) - that is the same pair! the same for orbitals (a,c) and (c,a)

0000_32_Product_Vee.png
Above: for a single term product function - the expectation value of energy:
The sum over coordinates becomes sum over orbitals (single particle)
The sum over coordinate pairs becomes sum over pairs of orbitals (pair operators)
Further:
Now turning to Slater determinant - which is a sum of N! products. Thus there are always (N!)2 terms (from "left and right" - double sum)
On the case of normalization check we see that the double sum reduces to a single one, because the terms where the two permutations
are not the same are zero, as indicated. There are thus only N! nonzero terms, and the normaliztion holds (due to the square root factor)

0000_33_Slater_Normaliz.png
Above: the overlaps, which needed to be identical to be non-zero - all N orbitals the same in each integral - this true for
all N! terms - can this apply also to the single particle terms.
See above how it was for a single product - there was a sum over some k of the the Hs ( rk ) and it yielded N different
orbitals. It must be same here, but only one thing unclear yet: will also here - for each k - i.e. Hs ( rk ) - the (N!)2 reduce
to the N! only non - zero - yes - see the last frame at the bottom of this frame:
the non-diagonals of Hs ( rk ) are non-zero, but since all the others in the overlaps must be paiwise the same ....

0000_34_Slater_Hs.png
So from the above discussion, the Slater behaves just as the single product for the single-electron operators.
Thus the sum over coordinates becomes sum over orbitals (single particle)
Now the pair operators;
again, the argument about the same orbitals remains valid, but now there is a double coordinate integral present
the N-2 orbitals in the overlaps must again remain pairwise the same
( as the one more N-1 orbitals in the single particle case )
but there is a difference - the "exchange term" appears for each permutation - but only once
- see the discussion towards the end of this slide

0000_38_Slater_Vee.png
There were N! permutations, thus there are N! equal terms in the summation over the pairs just above.
So that for Slater determinants
The sum over coordinate pairs becomes sum over pairs of orbitals (pair operators) each term in the sum
consists of a direct term and an exchange term

0000_39_Slater_Overview.png
Above:
The sum over coordinates becomes sum over orbitals (single particle)
The sum over coordinate pairs becomes sum over pairs of orbitals (pair operators)
each term in the sum over pairs
consists of a direct term and an exchange term
Below: firstthere is a sketch of the tasks sometimes used in introductory mechanics - or statics
the shape of a beam under deformation due to a force of weight or similar
In such problems the virtual works were introduced
This became a starting point of variational approaches in classical mechanics
c.f the Euler-Lagrange equation - and the calculus of variations
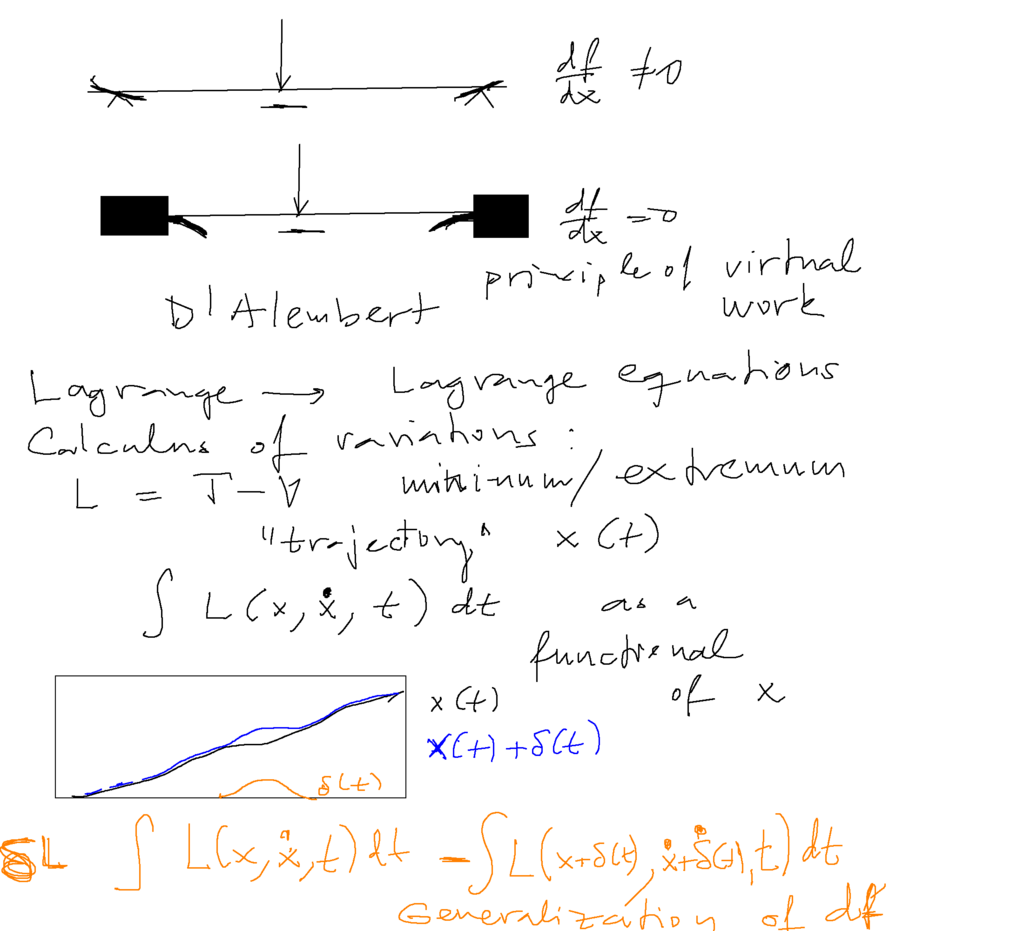
0050_origins_virtual_work_etc.png
Another background general history - minimum of a "landscape" function
But minimum on a given curve given by g(x,y) =0
Lagrange multiplier

0060_Minima_with_constraint_lagrange_mutplier.png
If we wanted derive the Schrödinger equation from a "variational approach" (why? - because it is so succesful in Class. Mech, )

0070_Variation_Schroedinger.png
Applying this to the N-particle energy
- we can claim the total energy to be extremal for the real (as we called "selfconsistent orbitals")
- with additional N constraints - the normalization of each orbital.
First we apply it without cosidering the exchange terms

0080_Variation_Hartree.png
when the exchange terms are left out --> the Hartree selfconsistent method follows
Next time:
Full Hartree - Fock equations