to index             2016_09_14 Previous lecture             LECTURE NOTE   2016_09_15           2016_09_21 next lecture note

Many-electron atoms - part 1.

Hund's rule - about spin states; in Carbon it is simply the same as triplet

0005_Hunds_rule.png        0005_Hunds_rule.png

Number of states in each shell ( n, l, m, ms   )        Closed shells - highest ionization energy

0006_numbers_of_states.png        0006_numbers_of_states.png

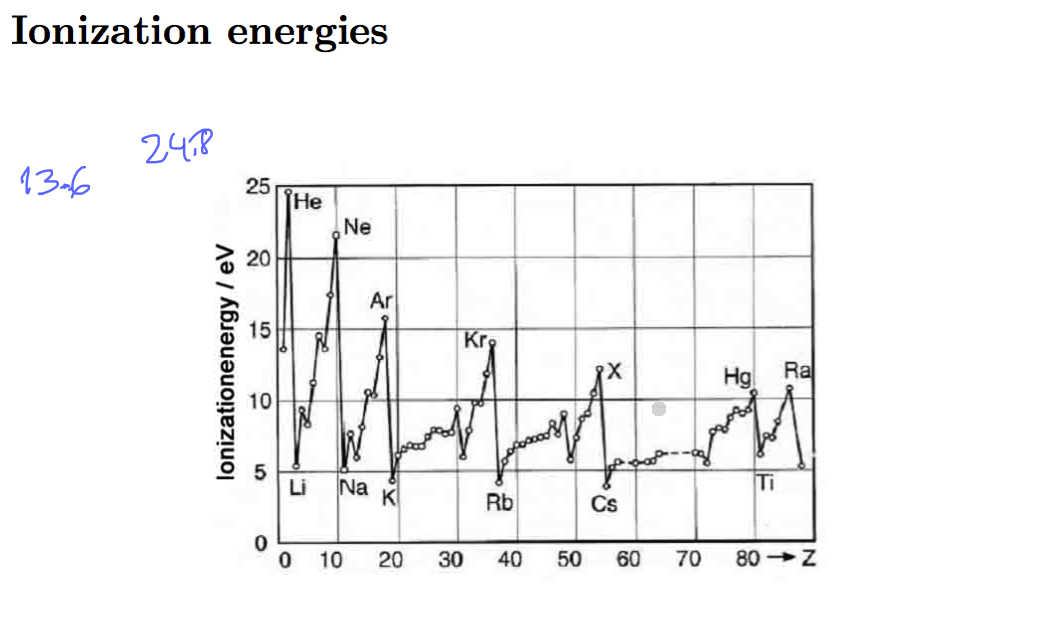
Closed shells - highest ionization energy   - but it does not follow Z= 2, 10, 28, 60,  ......                                                                                                but     Z= 2, 10, 18, 36,  ......

0007_ionization-energies-potentials.png        0007_ionization-energies-potentials.png

Here are the first ionization potentials and electron configurations for elements up to 58

0009_configurations_to_Argon.png        0009_configurations_to_Argon.png

ionization potentials and electron configurations ....

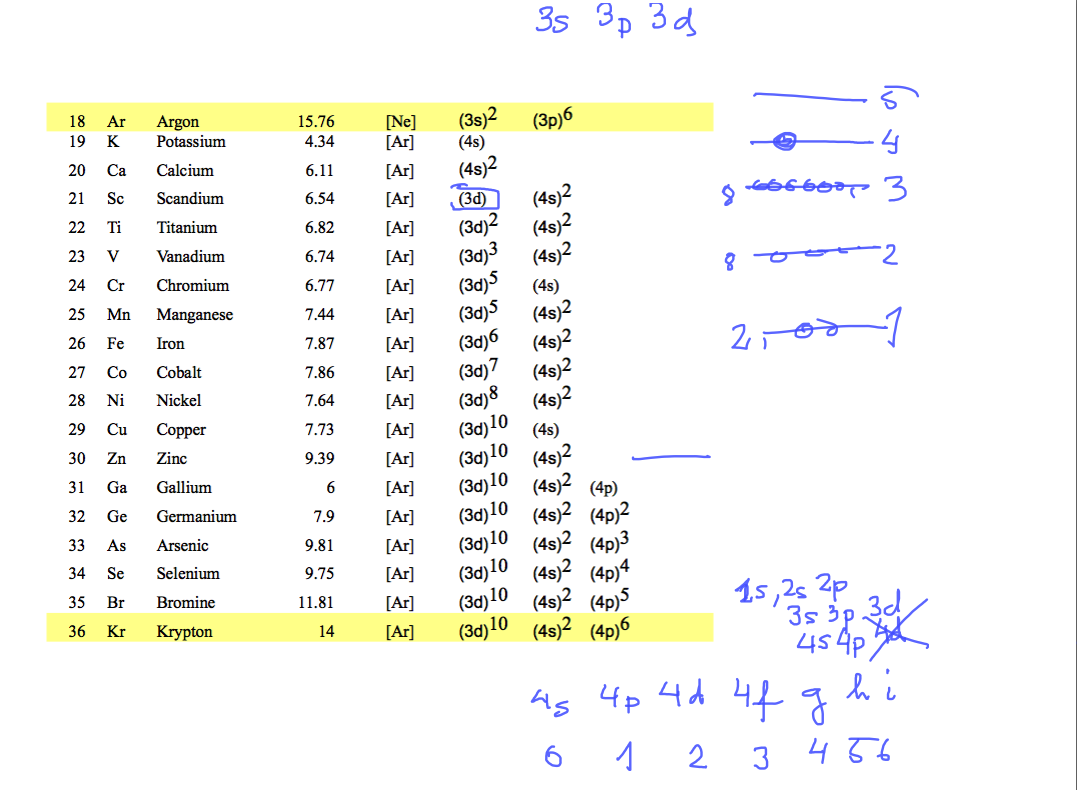
0010_configurations_to_Krypton.png        0010_configurations_to_Krypton.png

ionization potentials and electron configurations ....

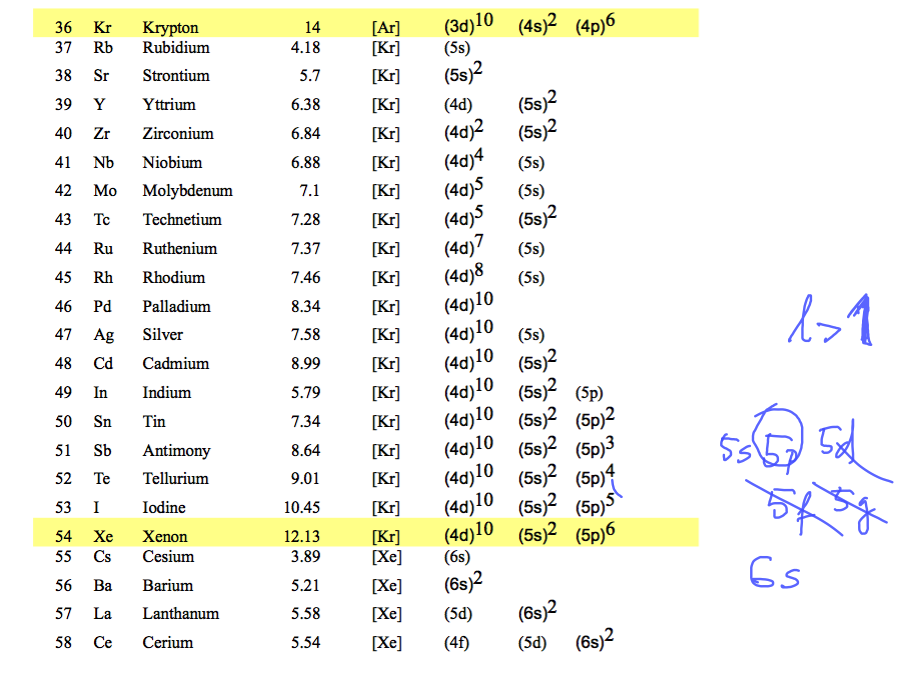
0012__configurations_to_Xenon.png        0012__configurations_to_Xenon.png

Why does the  4s   fill  before  3d?   i.e.        E4s   <   E3d             E5s   <   E4d            E5s   <   E4f                                                                                                                                        Hydrogen like    Enl  = - Z n -2  E0  independent of L              Because the potential energy of the "last electron" is not  the   r-1  , not  Hydrogen like   (see the screening  discussion further down)     Radial potentials with added "centrifugal term", i.e. the kinetic energy of rotation, from angular momentum     Coulomb compared with the screened potential   -  note that Coulomb accomodates the     Enl    independent of L     Clearly, the screened can not give the same behaviour of    Enl     - so it must depend on L  - and there is a dramatic change                                                                                                                from L=1    to   L=2    (  and larger L )

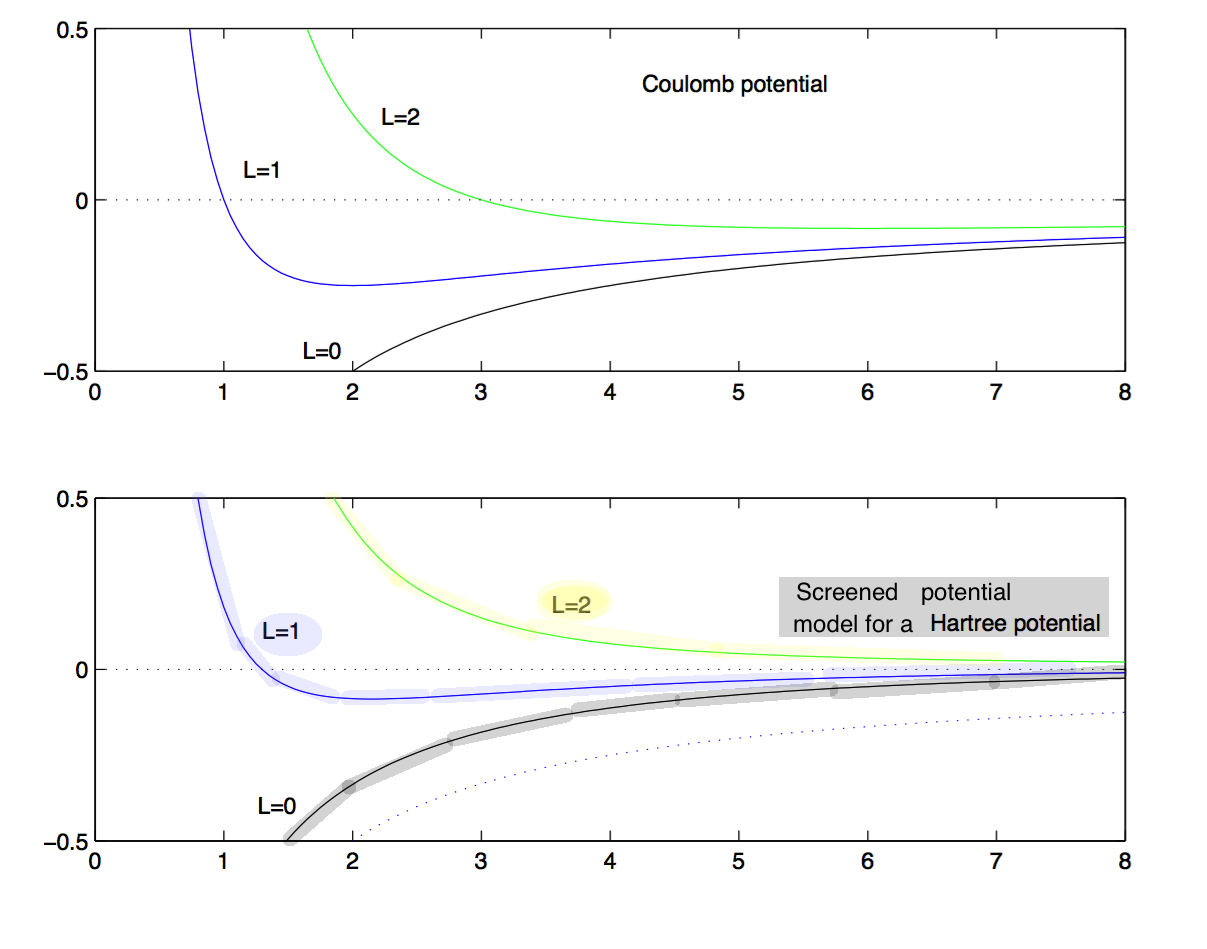
0013_Screened_potential_explains_d-states.png        0013_Screened_potential_explains_d-states.png

The above superimposed

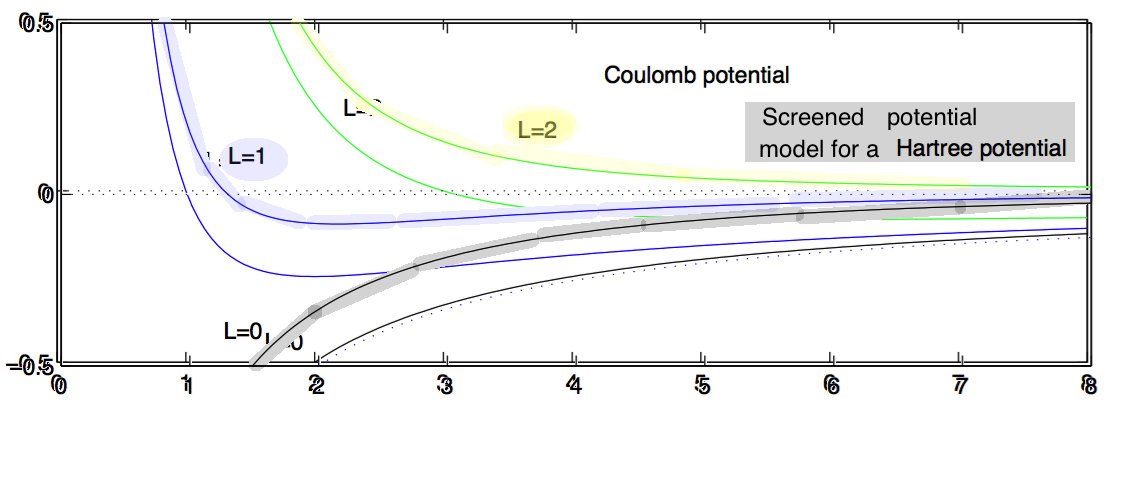
0014_Screened_potential_superimposeds.png        0014_Screened_potential_superimposeds.png

The shape - a model - for the screened potential

0016_Coulomb_Centrifugal_screened.png        0016_Coulomb_Centrifugal_screened.png

The shape - a model - for the screened potential explained.   Close to the nucleus - only the Z-charges Coulomb force                                                                                                        Far away - the "last electron"  sees only charge 1                                                                                                        the transition - exponential function damping ( model ! )        Also discussed the concept  " classical turning point "

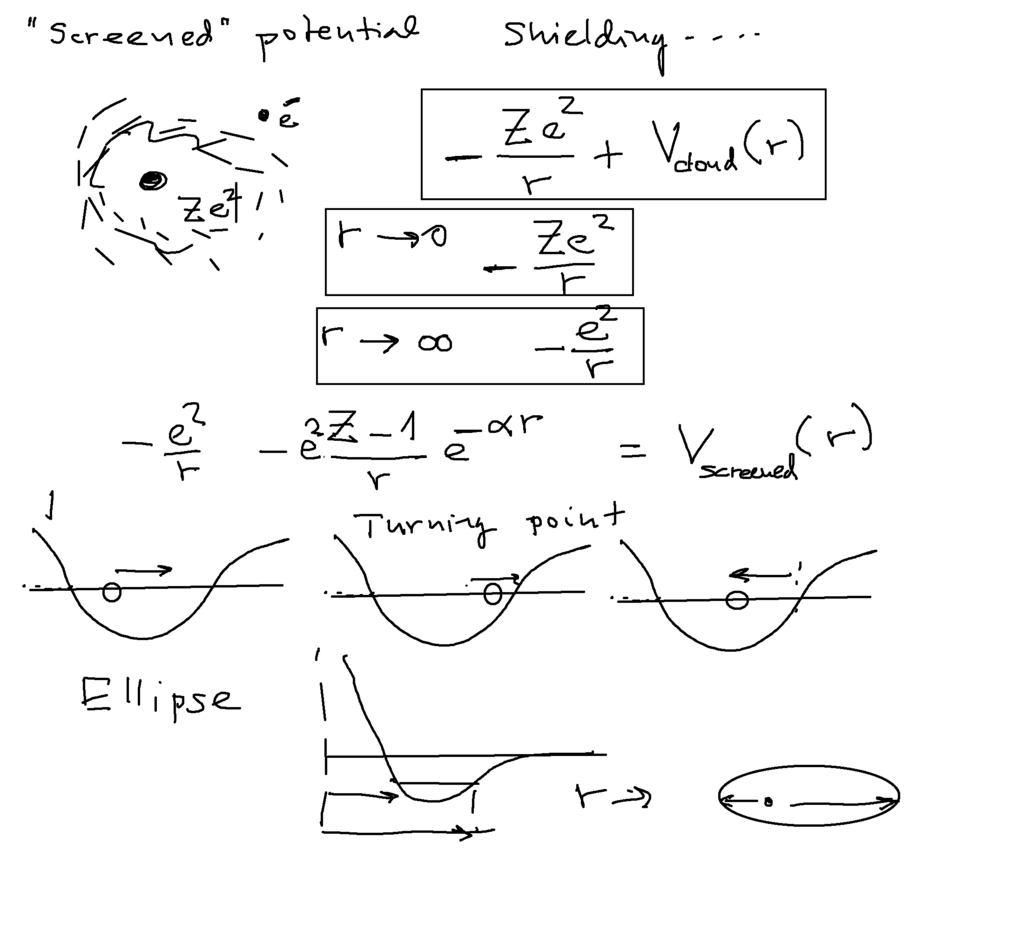
0018_Screened_potential.png        0018_Screened_potential.png

Interaction with a "charged cloud" - towards the selfconsistent potential model

0020_Interaction_with_a_charged_cloud.png        0020_Interaction_with_a_charged_cloud.png

Charged density from probability density - electrons in occupied orbitals   The Schrödinger equation must be solved for obtaining all the orbitals

0110_SCF_1.png        0110_SCF_1.png

Iteration scheme

0120_SCF_2.png        0120_SCF_2.png

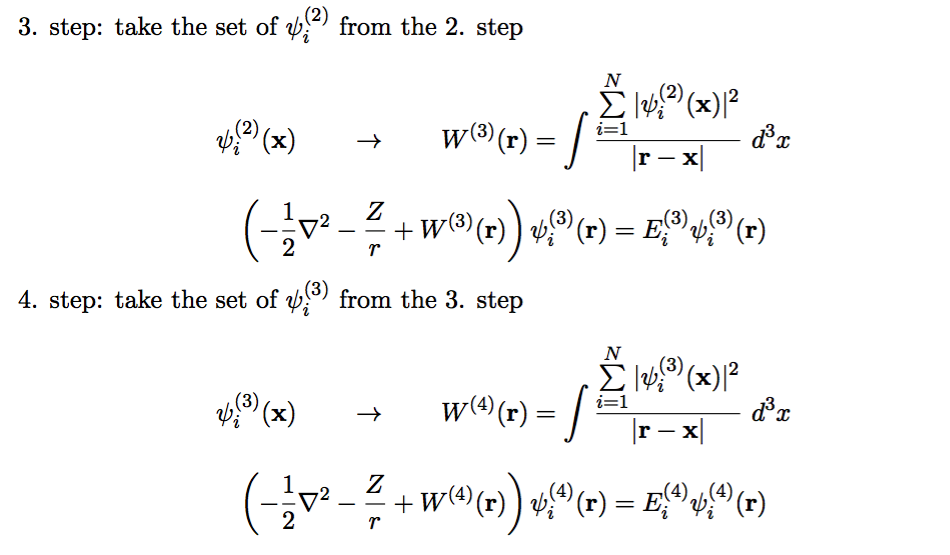
0130_SCF_3.png        0130_SCF_3.png

Iteration scheme    -  how to stop it  -  when the potantial and the orbitals are "self consistent"

0140_SCF_4.png        0140_SCF_4.png

The above Hartree - inspired construction is a qualitative and intuitive efficient model - can it be derived precisely?      Formal derivation of many-electron madel - Hartree-Fock method       This starts by evaluation of expectation value for the hamiltonian       Helium   N=2       Lithium   N=3        -  and general N          antisymmetric function for N-fermions

0200_SThis is based on elf_consistent_formal_derivation.png        0200_Self_consistent_formal_derivation.png

Helium already discussed in a previous lecture

0210_Helium.png        0210_Helium.png

Slater Determinant                                                                     PERMUTATIONS, Combinatorics, number of permutations of N objects   N!

0220_Determinant_Slater.png        0220_Determinant_Slater.png

0230_Slater_3x3.png        0230_Slater_3x3.png

above  - permutations   -  odd and  even       Lithium case  - there are many  terms  (118 pair terms - how to organize them )

0240_Lithium.png        0240_Lithium.png

Next time:   Lithium     and       N > 3  - general case

to index             2016_09_14 Previous lecture             LECTURE NOTE   2016_09_15           2016_09_21 next lecture note