Helium - part 4: Hylleraas variational function, Doubly excited states, Exchange interaction
The previous lecture about the variational method assumed a product function, i.e. independent electron.
Hylleraas proposed a function which can not be factorized as a product of two functions of the two coordinates
Not independent - therefore correlated
somewhat surprising implementation of the correlation - see below

0005_HYLLERAAS.png
Not independent - therefore correlated
somewhat surprising implementation of the correlation
constructing expressions of the two variables
First we explore the product and not product - already a sum of two or more products is NOT a single product

0010.png
Last idea above: the simple "correlation" could be a function of the DISTANCE between the two electrons. Just the simple f(x) discussed,
where x is the indicated distance between 1 and 2 would be a good first step - suppressing the wavefunction as x --> 0
(simulating repulsion)
This is indeed one of Hylleraas' extra variables;
Hylleraas used 6 variational parameters - as illustrated
Later, with computers arriving: The best calculations used up to 1023 variational parameters and obtained great accuracy
in comparison with experiments

0020_HYLLERAAS.png
Correlation by configuration mixing
This idea could follow from the above consideration of sum of products, but it follows also quite formally
from the expansion theorem as illustrated
They cn be obtained by linear algebrahe unknown coefficiens d below are not searched by a particular variational method,
since they are linear - they can be obtained by DIAGONALIZATION - the well known method to find eigenvalues

0040_Configuration_mixing_--Expansion_eigenfunctions.png
Configuration mixing visualization - for 2 electrons - and for "many" electrons (i.e.4)
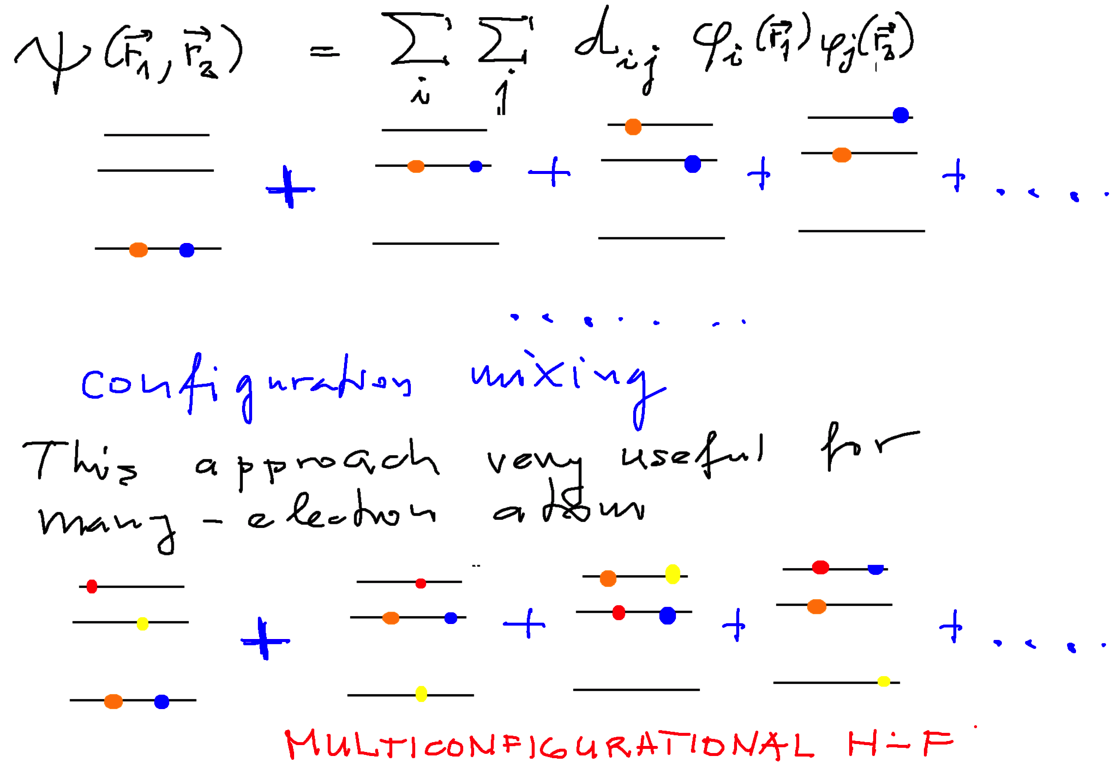
0050_Configuration_mixing.png
Exchange interaction - consider the TRIPLET and SINGLET as before, but now we really evaluate
the expectation values of the hamiltonian
We first show the normalization
Then how the many terms ( 12 terms with the factoring of H into H1, H2 and V12 ) reduce to 4 terms
where the last one is the "exchange term" - leading to the exchange interaction
1. normalization - and the H1, H2 behaving as in the normalization evaluation -
factors 2 cancel

0060_origin_exchange_interaction.png
Exchange interaction - see the difference between singlet and triplet, normalization included
2. triplet, singlet explicitely

0070_origin_exchange_interaction.png
Exchange interaction
3. summary - SINGLET - TRIPLET difference now from a formal expression
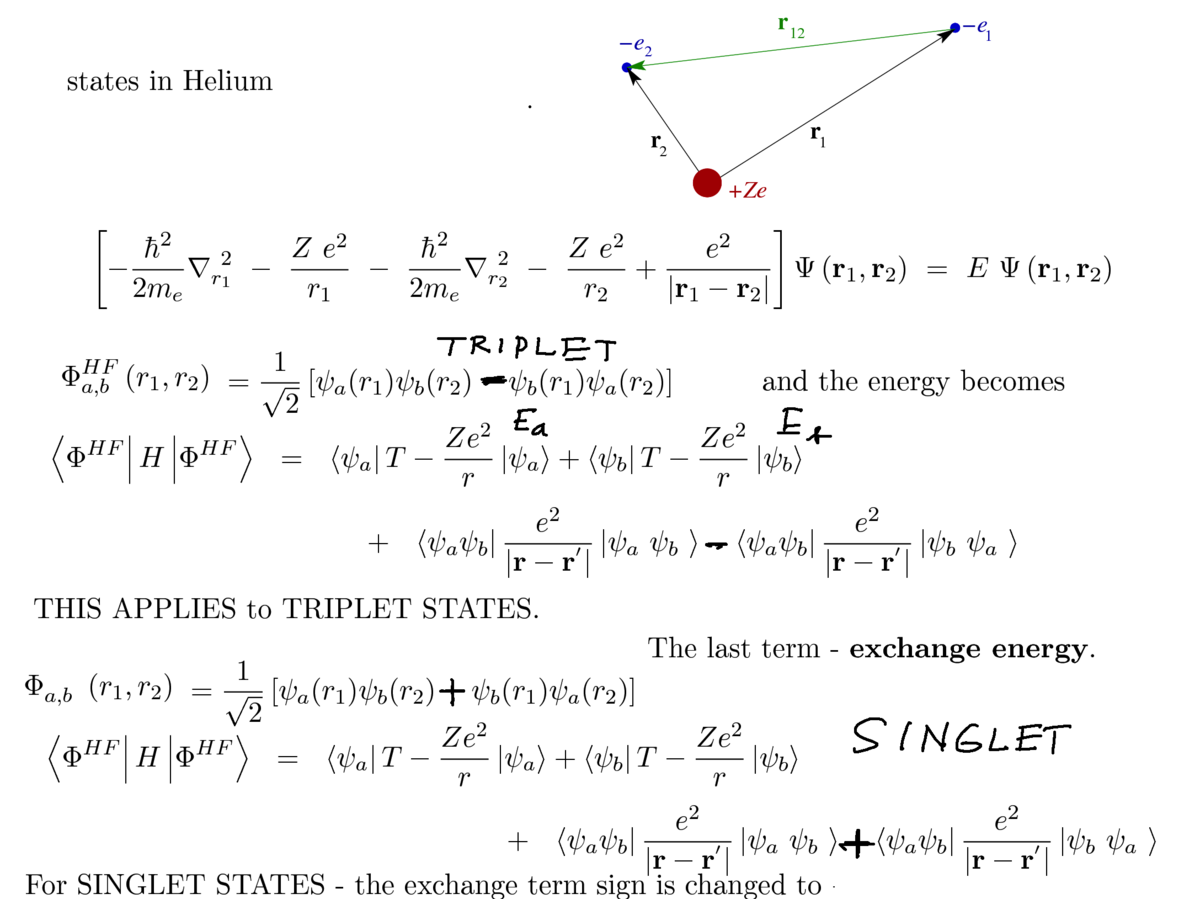
0080_triplet--singlet_exchange_interaction.png
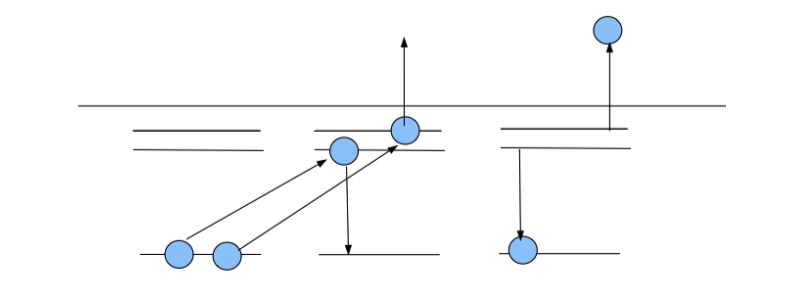
Doubly excited states of Helium
the previously discussed orthohelium - parahelium states - only one electron excited, as indicated
if both orbitals are excited states - the resulting state probably has the same energy
as "continuum states", i.e. such states that one electron is bound and the other escabed - free

0110_Double_excited_states.png
The original version (a textbook) of our above picture

0120_Double_excited_states.png
Schematics of Autoinization, Auger process and electron-scattering resonances
(resonance - enhancement fora particular frequency - in Q.M. - a particular energy )
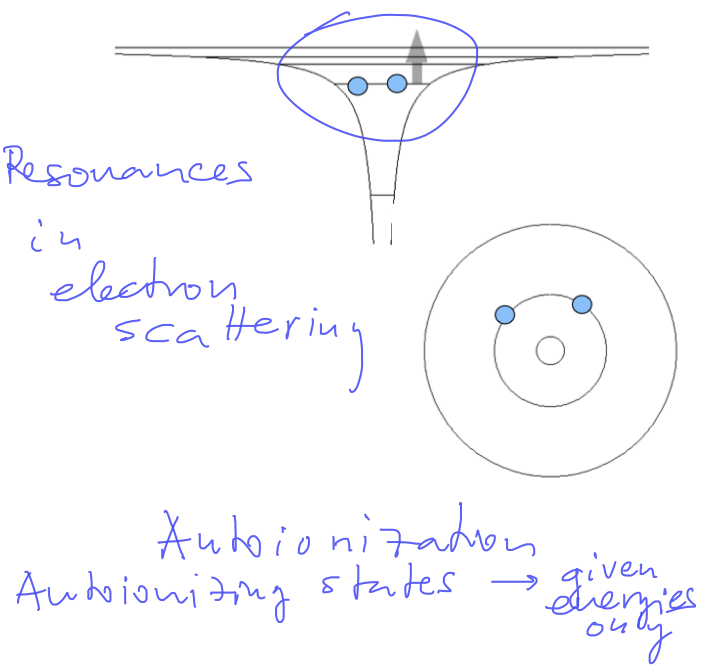
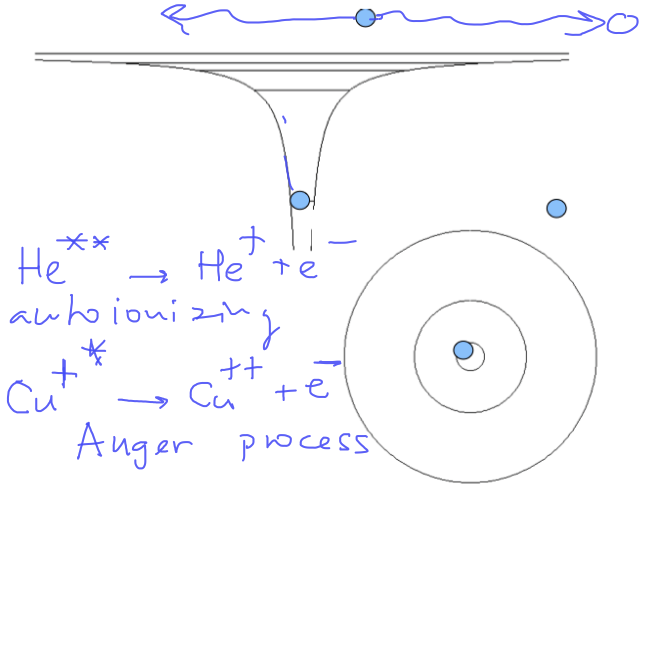
0130_Double_excited_Autoionization.png 0140_Double_excited_Auger.png
Another schematics of autoinization - doubly excited states - LATER in the course: non-radiative processes
0150_Double_excited_schematic.png
Exchange interaction --> effective spin-spin interaction
Purely formally, as far as the electrons are in given orbitals, the energy difference between singlet and triplet
can be formalized as an "effective spin-spin interaction" - favoring the parallel spins - as shown below

0160_Spin-Spin.png
Exchange interaction --> effective spin-spin interaction
Purely formally, as far as the electrons are in given orbitals, the energy difference between singlet and triplet
can be formalized as an "effective spin-spin interaction" - favoring the parallel spins - as shown here
But it turns out that exactly this is the correlation leading to FERROMAGNETISM in certain solid state
materials

0163_Spin-Spin.png
Exchange interaction -- this is the correlation leading to FERROMAGNETISM in certain solid state
materials - final arguments

0165_Spin-Spin.png
... and we started to look at Many electron atoms --> NEXT TOPIC