In this lecture we started by reviewing some of the last lecture, but concentrating mainly on the approximations
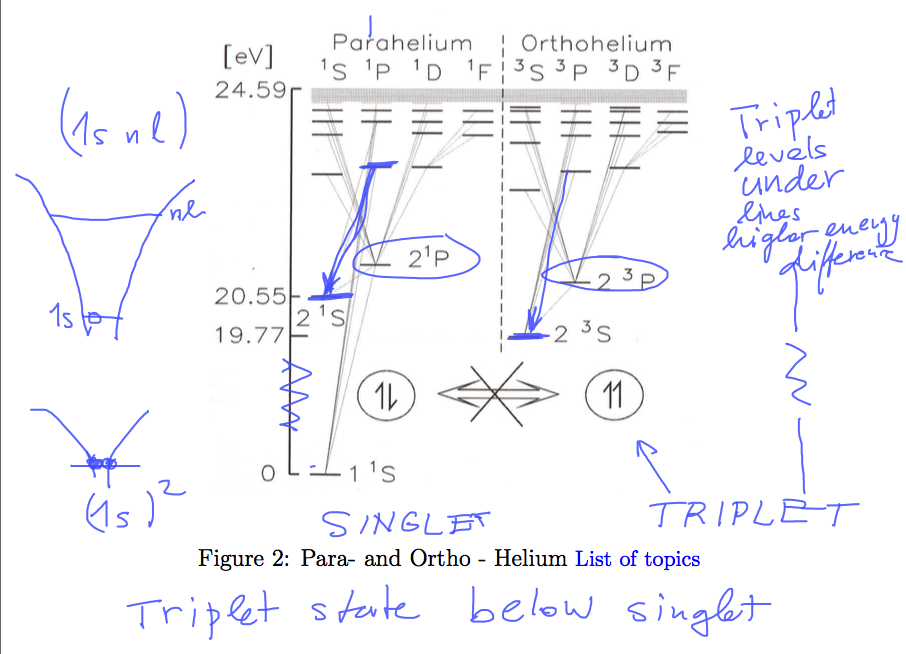
While the ortho - para problem from last lecture is about the EXCITED STATES of helium, this lecture is mainly
on the GROUND STATE, i.e. the two electrons are as much bound as possible, both close to the
1s state hydrogen-like with - with nucleus charged Z-times -- for helium Z=2
Homework: consider the statement:
The triplet states (type 1s nl ) (orthohelium) are more bound (deeper bound) than corresponding
singlet states (smae 1s nl ) (parahelium)
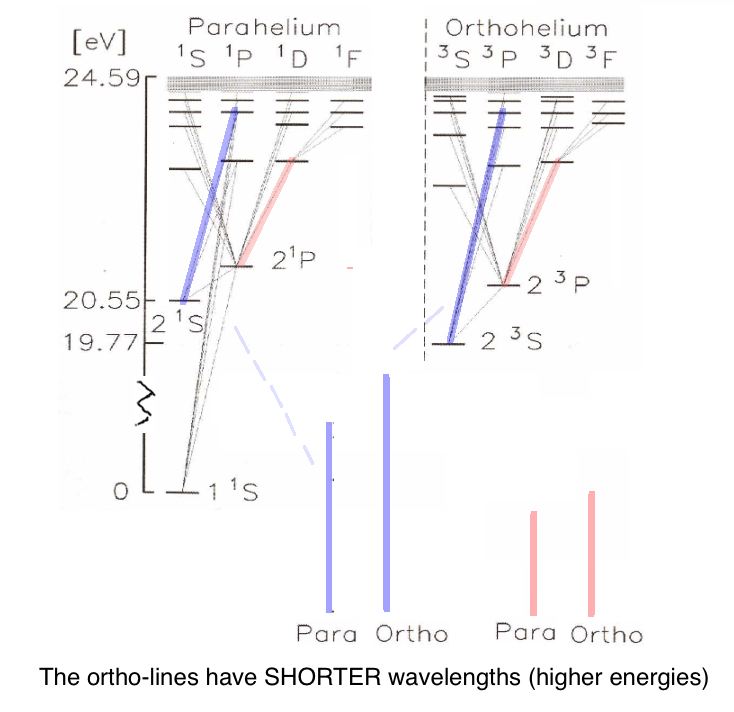
Thus all the orthohelium lines have all slightly shorter wavelength (higher transition energy)
then the corresponding parahelium lines
You should be able to explain this statement.
Below is the plate used for discussion, there is also a copy (cut) from 2015 plate: ../2015_08_27/0320_ortho_para_helium.png
in the last year's lecture ../2015_08_27/index.html
0002_triplet_singlet_revisited.png 2015_ortho_para_helium.png
We recall the energy - hamiltonian of previous lecture - the separation into "two hydrogen-like 1 electron subsystems"
- when the electron - elctron energy V12 was left out
Now we do the "1. order energy perturbation theory" with the same wavefunction: 2 1s electrons with Z=2
This is done by evaluating the expectation value.

0010_approximations_repulsion_perturbation.png
The repulsion integral - using multipole expansion

0013_repulsion_expect_evaluate.png
The evaluation is simple, but it takes lots of time

0015_repulsion_expect_evaluate.png
Angular inegrals are all zero due to the 1s --> L=0 M= 0 except tre one with L=0 M= 0 - which is ONE as indicated
The radial intgration - with the meaning of the symbols r> and r<

0016_repulsion_expect_RADIAL.png
The evaluation is simple, but many steps ...

0018_repulsion_expect_RADIAL.png
Here is the summary of the evaluation

0019_repulsion_expect_FINAL.png
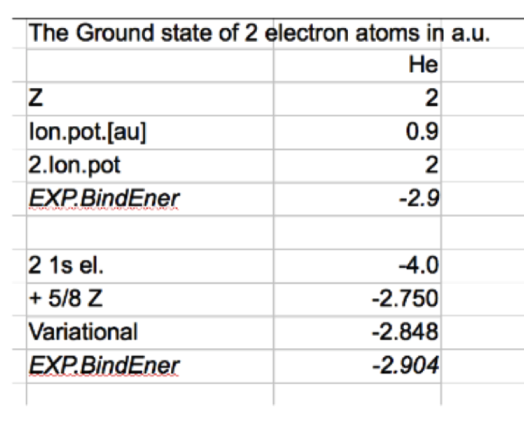
For any Z value the 2 electrons in 1s state each have expectation value of their repulsion given by the expression above.
Below we compare with experiment 2x (1s) means the simple hydrogen-like, with Z=2 and without repulsion
adding the expectation value of the repulsion - much closer to observed values
Note: the energy of netral HJe = 1. ionization potential + second ionization potential - as indicated
Towards the end: suggesting "Effective Z"

0030_approximations_repulsion_perturbation.png
The idea of effective Z - but how to find that Z ?
General theorem comes to help: expectation value of energy in the ground stat is smaller (or equal)
THAN for ANY state, whasover, whether it only peaks over the deepest potential regions, whatver

0040_Theorem_for_minimalization.png
The above theorem is the basis for variational method - stated below
We use parametric dependence - search for best function --> search for minimum Zeff --> z variable

0050_varying_the_wavefunction.png
The actors - 1s state, kinetic and potential energy;
Z - dependence and z- dependence The nucleus has Z, the wavefunction has z

0055_variational_method.png
Z - dependence and z- dependence The nucleus has Z, the wavefunction has z
Here we derived Zeff --> z = Z - 5/16 ( in He the Zeff is about 1.7 )

0060_variational_done.png
Comparison of the numbere, results 2x (1s) means the simple hydrogen-like, with Z=2 and without repulsion
and "1. order energy perturbation theory" with the same wavefunction: 2 1s electrons with Z=2 i.e. + 5/8 Z
and Variational - above
results_eV.png 0069_results_a.u.png

NEXT: Better variational - more advanced searches - and variations with correlations
configuration mixing, other 2-electron ions