Exchange Symmetry - as explanation of Pauli Principle - and Aufbau (build-up) principle for more-electron atoms
To "get" the Pauli principle - physicists postulated the identical particles - indistinguishable particles.
Via probability - and independent particles in orbitals
Exchanging particles must lead to the same probability (see below)
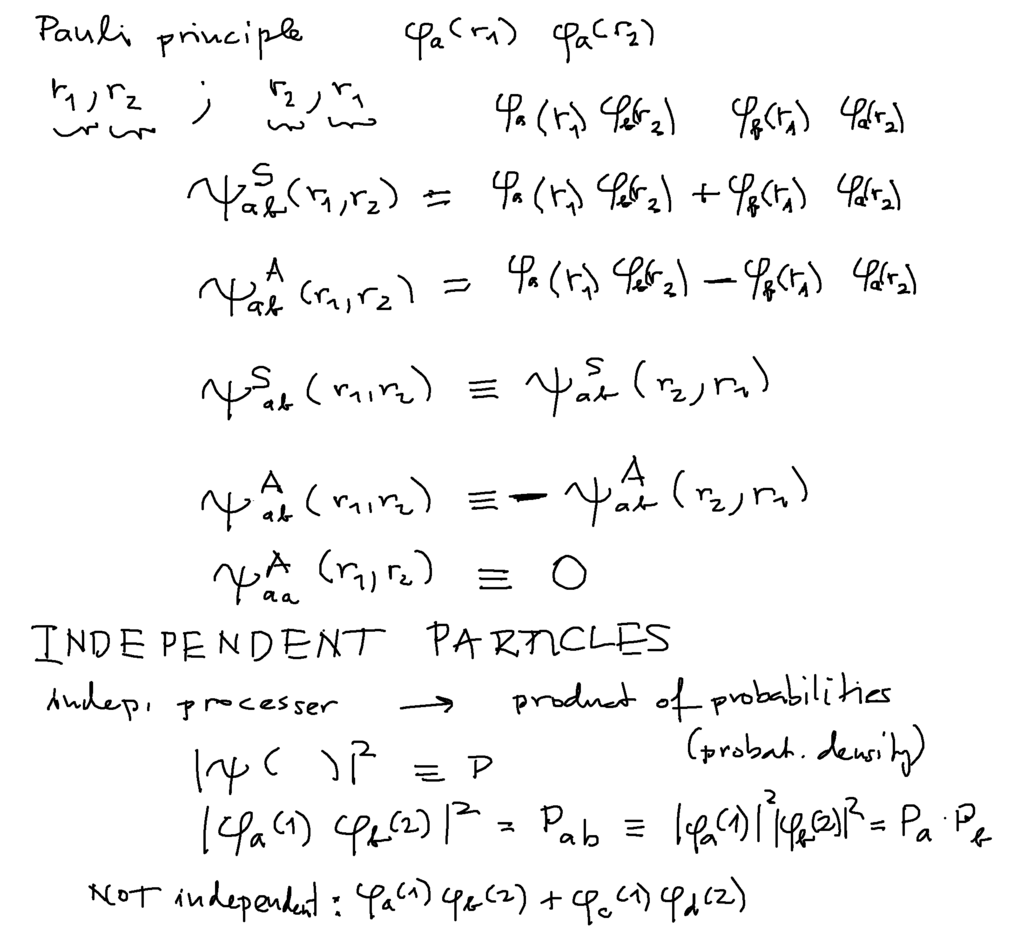
0010_Pauli_Principle--Symmetry_Indep_particles.png
above: Missing one statement if indistinguishable P( r1, r2) = P( r2, r1) P( r1,r2) = | Psi ( r1, r2 ) |2
THUS Psi( r1, r2) = Psi ( r2, r1) called Symmetric
or Psi( r1, r2) = - Psi ( r2, r1) called Antisymmetric
Below: This can be formulated formally defining exchange operator
Homework: applying exchange twice - we get identity
Eigenvalues of exchange operator can thus be +1 or -1
Below further: Electron Spin ( not really angular momentum - rather magnetic moment )
magnetic moment associated with angular momentum
BUT the proportionality constant is TWICE as large for the spin ( Landé factor )
The physical dimension of angular momentum : the same as the Action (classical mechanics), as Planck constant ( hbar )

0020_Electron_spin___starts_exchange_operator.png
Wavefunction for spin
Wavefunction for two spins
Wavefunction for spin and space
Antisymmetric and Symmetric combinations - ANTISYMMETRIC total for two electrons
SURPRISE - the straightforward antisymmetry for 2 total (space and spin ) functions is not the "right" answer
spins - move independently of space motions of the two - thus product of 2 spin function and 2 space functions

0030_antisymmetry_surprise_independent_L_S.png
This is found - and confirmed by experiment - space part nd spin part are "independent" - thus the PRODUCT wavefunctions

0032_antisymmetry_independent_L_S_TEXT.png
So what about two spins - 4 possibilities single one antisymmetric - three symmetric combinations
This snapshot from the notes

0033_Two_Spins_products.png
Product wavefunction of spins and space motions from the lecture
SInglet and triplet
The ground state must be a SINGLET - because the two electrons must be both in the same lowest possibility of space motion
space function symmetric - thus spin antisymmetric - spin SINGLET

0040_singlet_and_triplet.png
SO all the excited TRIPLETS are energetically bellow the excited SINGLET - explained below
TRIPLETS are ORTHOHELIUM and SINGLETS are PARAHELIUM (it is in spectrum only)
But no radiative "lines" from triplets to GROUND STATE (because the spins are arranged differently)

0041_Repulsion_weaker_in_Triplet.png
WHY ORTHO and PARA the triplets can not be reached by electromagnetic (single electron processes)
only via free states or collisions and re-arrangements
then populated statistically
there are 3 times as many triplets. Triplet lines more usual - so ORTHO (like in orthodox)
Singlet lines three times weaker, thus less usual - PARA (as in paranormal, parapsychology ... )
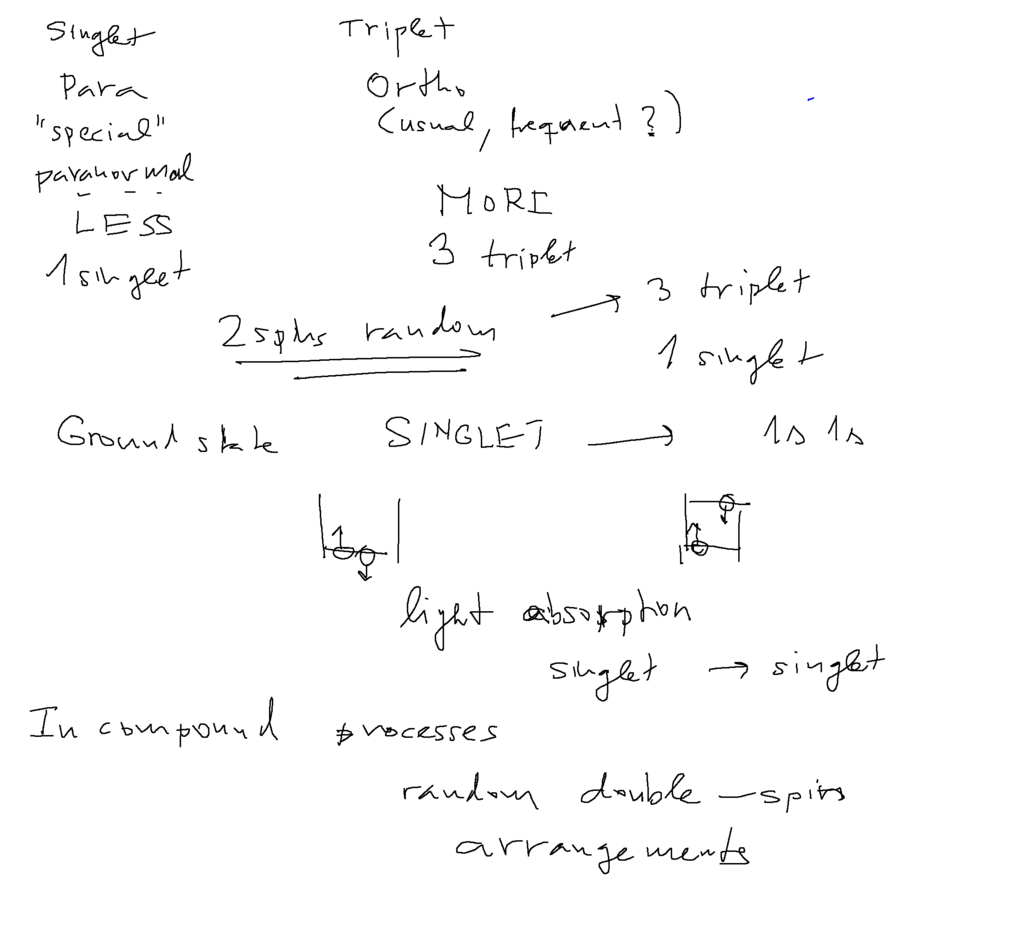
0050_why_ortho_and_para_hypothesis.png
Electron motion in helium - no analytic solution --> THUS approximations
The simplest "method" is toneglect the repulsion - can not be a very good approximation - but we shall improve it later
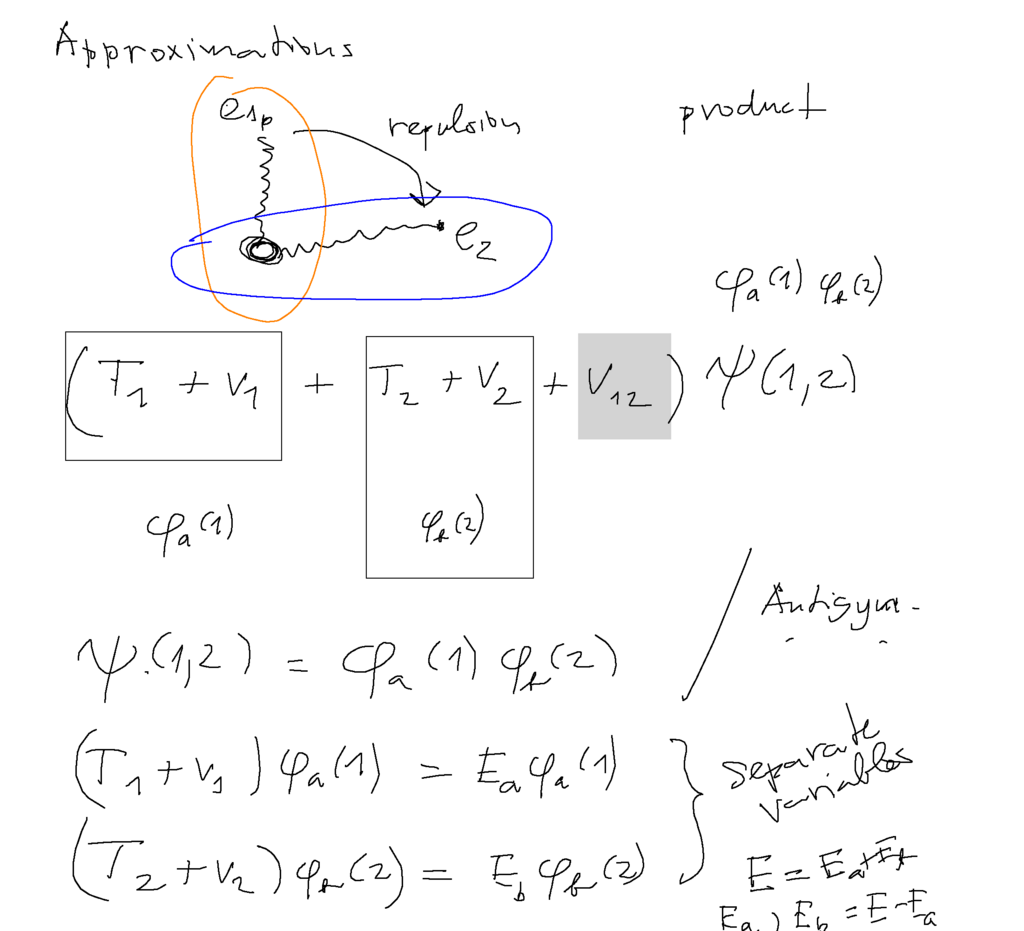
0060_Starting_Approximations.png
independent electron model for Helium - with repulsion included --> Next lecture