PHYS261 - autumn 2015

to index 2015_08_26 Previous lecture note LECTURE NOTE 2015_08_27 2015_09_02 Next lecture note

Atomic units and Helium - Introduction

An important part of physical approach are the systems of units, which are suitable for the studied systems.
Units suitable for the everyday life are not suitable for description of astronomical objects, and they are also
little suitable for the world of atoms and molecules. So the units are important, in spite of what some theoreticians
from time to time claim, for example introducing "natural units" which then "remove" all the "unimportant" constants.

First we look at the units, then we start our approach to the physics of Helium and two-electron atoms.

The first "atomic unit" - most famous - is the radius of the first orbit in the half-classical Bohr's first model of the atom.
This unit of length can be obtained by various arguments - some are shown in the first slide note.
The Bohr radius

0094_Atomic_units.png

after the Bohr radius is chosen as unit of length, we need two more. We can chose the energy and the time.
When dealing with energies, half way to suitable units is to use the ELECTRONVOLT - 1 eV - as a useful unit.
This is because the electronvolt is used in many connections ( warning: the chemists use a unite close to 1 eV,
but different. It is called kiloJoule per mol
1 kJ/mol -> 0.010364 eV (per particle)
1 eV -> 96.48 kJ/mol ( 23.06035 kcal/mol )
Note that the Coulomb energy expectation (27.2 eV), and not the H-atom binding (13.6 eV) is chosen for energy unit
(some people did just that, using 13.6 eV; this mixes things up a bit, see below, the Wikipedia case)

We calculate below the convenient atomic unit of time : it is 25 attoseconds - or 0.025 femtoseconds

0098_atomic_units_energy_time.png

Above - the usual and most reasonable choice of "atomic units.
Below - the confusion which can result from a "seemingly convenient" choice.
The difference is what one selects - should we have a 1/2 in the definition - or not.

The below quoted writers take this literally as two different choices - an absurd story results,
- who claim that these two choices "differ in the choice of the unit of mass and charge
https://en.wikipedia.org/wiki/Atomic_units
Below is shown that just the 1/2 is sort of misplaced.
The natural units "equation" is another absurdity often found in print .....

0099_Hartree_Rydberg_wikipedia.png

0099_Hartree_Rydberg_wikipedia.png

Helium and two-electron atoms.

The two-electron Quantum Mechanics - is simply more complicated than the hydrogen atom case.
Six coordinates, 2 kinetic energies and THREE potential energies;
One part of the potential energy is the electron-electron repulsion.

Last time we worked with VARIABLE SEPARATION into two ( independent - if lucky ) equations.
In He - not possible, due to the repulsion, which "mixes" the variables

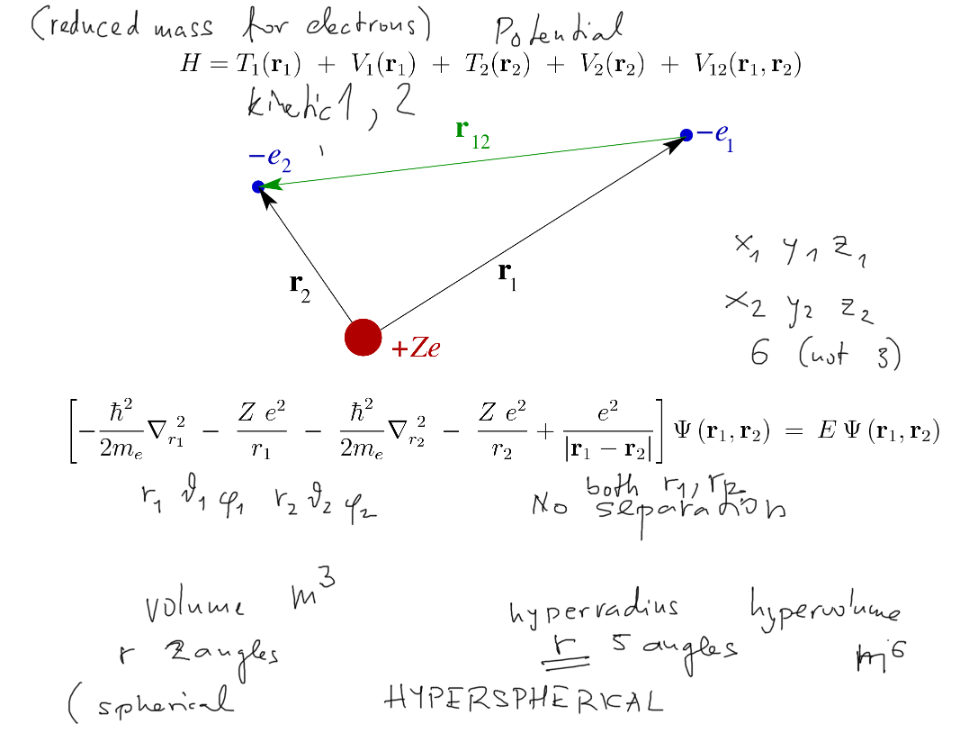
0100_He_coordinates_Hamilton.png

He atom - not exactly analytically solvable!!
Approximations necessary
we start by - for a while - neglecting the "complicating" electron repulsion.

Then we can do the separation - assuming that the solutions are products of function of each variable
Product --> independent particles -- as we shall discuss next time

With the separation -- approximation that each of the two electrons obeys
its own hydrogen-like Schrödinger equation
(two "parallel hydrogen atoms")

0110_Independent_electrons_Separation.png

OK - if this were the case - what about binding energy of the He ground state (two "parallel hydrogen atom ground states")

The energies are shown below (together with better approximations)
We see that this idea fails badly.
Total binding in He ground state is 79 eV, it takes 24.6 eV to make free the first electron (singly ionize), and the
second is hydrogen-like - to remove that is 4 times 13.6 eV --> 54.4 eV, thus the total 79 eV (experimental results)
Our "approximation" give twice 54.4, it means 108.8 eV.

We shall improve this next time, when we shall try to include the electron-electron repulsion in a somewhat better
version of outr approximation

0200_n_Energies_Approximations.png

Once we summarize what we do not understand, let us have a look at He spectra - and level schemes.
The old experimenters actually believed there were two "versions" of helium, which they called
orthohelium and parahelium (quite confusing names); but one should add that they were looking at
the transitions close to visible ... more on this when we treat this in detail

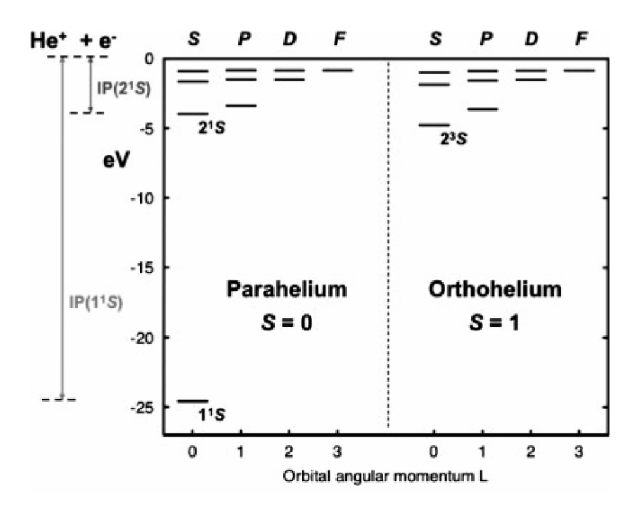
0300_ortho_para_helium.png

The orthohelium - parahelium differences indicate that the approximation ideas based on completely independent electrons
can not be really accurate - here we have the levels in some more detail.

Note again that the spectroscopist only "sees" the transition lines (wavelengths). The level schemes must be constructed.

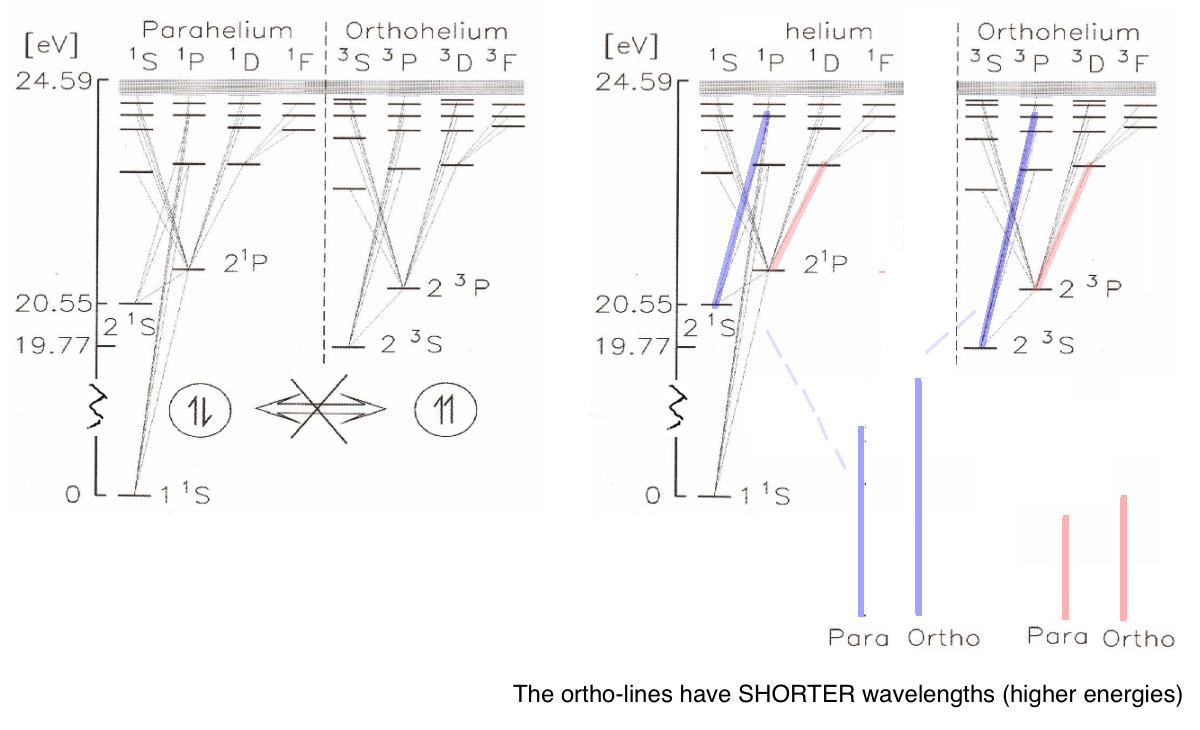
0320_ortho_para_helium.png

We will come back to this - the keyword is the role of electron spin - via the Pauli principle and "exchange symmetries".
Next time we continue with the GROUND STATE - starting with the electron repulsion calculations.