See also the PDF-note He_and_2-el_atoms.pdf
Last time we started by considering the oversimplified model - cutting away the electron-electron repulsion
In this lecture we consider a less drastic approximation - putting it on a more formal basis
First we had a look at the last introduction part - and discussed some details of polar plots.
The plots we looked at once more:
Finally we discussed the separation of variables - product wavefunction - but since the quation is LINEAR,
a sum of solutions is also a solution. THIS IS IN PARTICULAR RELEVANT for hydrogen, where we have
DEGENERATE energy eigenvalues - it means there are several different (linearly independent) solutions for
the same - degenerate - energy value (degenerate eigenvalue) E(n,l) for different l have the same energy, given by n
He ground state - perturbation theory - starts on the next plate

xcf_0000-Explaining_product_radial_angular.png
We often speak about independent electrons, particles - and use it as synonym for wavefunctions
which are products of parts that are functions of each particle's coordinates separately.
This is the story of separation of variables again - to get it from Schrödinger equation - we must consider
a hamiltonian with the interaction between particles are "switched off" (or "neglected" - neglected only during the
first stage - inventing the model). The interctions are then "switched on" in the next stage - see below - Perturbation theory

xcf_0010-Independent_Particles--Product_wavefunctions_probab.png
of a problem where the solutions are known (i.e. a simpler system - instead of H this system described by H0
Also mentioning the Dirac notation expectation values; Linear algebra notation in mathematics often only parantheses, not bra-kets
Then we start explaining the perturbation theory ...

xcf_0020-Perturbation--Expansion.png
i.e. with the same POWER of lambda (and then set lambda to 1, or simply cancel it)
This gives equations for CORRECTIONS of different ORDER. (we remain here at the first order for the energy)
We also see that this first order perturbation energy correction leads to energy value ( E0 + E0(1) ) which is the same
as the EXPECTATION VALUE of the total H calculated for the unperturbed phi zero.
Then we apply all this to He ground state
(in the last line of this plate)
In the yellow frame: we remind ourselves that in fact in physics
we usually have function of dimensionless quantities
sine of five kg is a nonsense -- what we really mean is
sin( m/mu ) where mu is the mass of 1 kg
Unfortunately, we often assume this so clear ......
This leads to such misfortunes as "natural systems of units"

xcf_0030-Perturbation-Ground_state_Helium.png
as the EXPECTATION VALUE of the total H calculated for the unperturbed phi zero.
In the last 2 lines above - all this is applied to the He ground state problem
Now we start evaluating the repulsion - i.e. its "expectation value" - or as discussed - the perturbation theory result
We start by repeating what 1s-state is - the formula from Introduction on hydrogen atom wavefunctions
( here we again put in light yellow frame the fact that these are functions of dimensionless variables, as r/ a0 )
( see the yellow frame and a comment above)
General method - Multipole expansion - see the meaning of r> and r<
the expression for 1 over the distance between two positions r1 and r2 appears in many applications
the mathematical trick is to expand it into a sum containing PRODUCTS of r1, r2 - separated terms

xcf_0040.png
Also the angle between the two r-vectors - theta-1-2 is mentioned, plus the meaning of r> and r<
Below is explained how to evaluate - General method - Multipole expansion
For our case, the GROUND STATE which contains only s-states, i.e. l=0, m=0 for both electrons, the sum in the
multipole expansion reduces to ONLY ONE non-zero term ( L=0, M=0; all the other ANGULAR integrals give zero )

xcf_0050.png
The answer for
< (1s)(1s) | Vee | (1s)(1s) > = 5 Z / 8
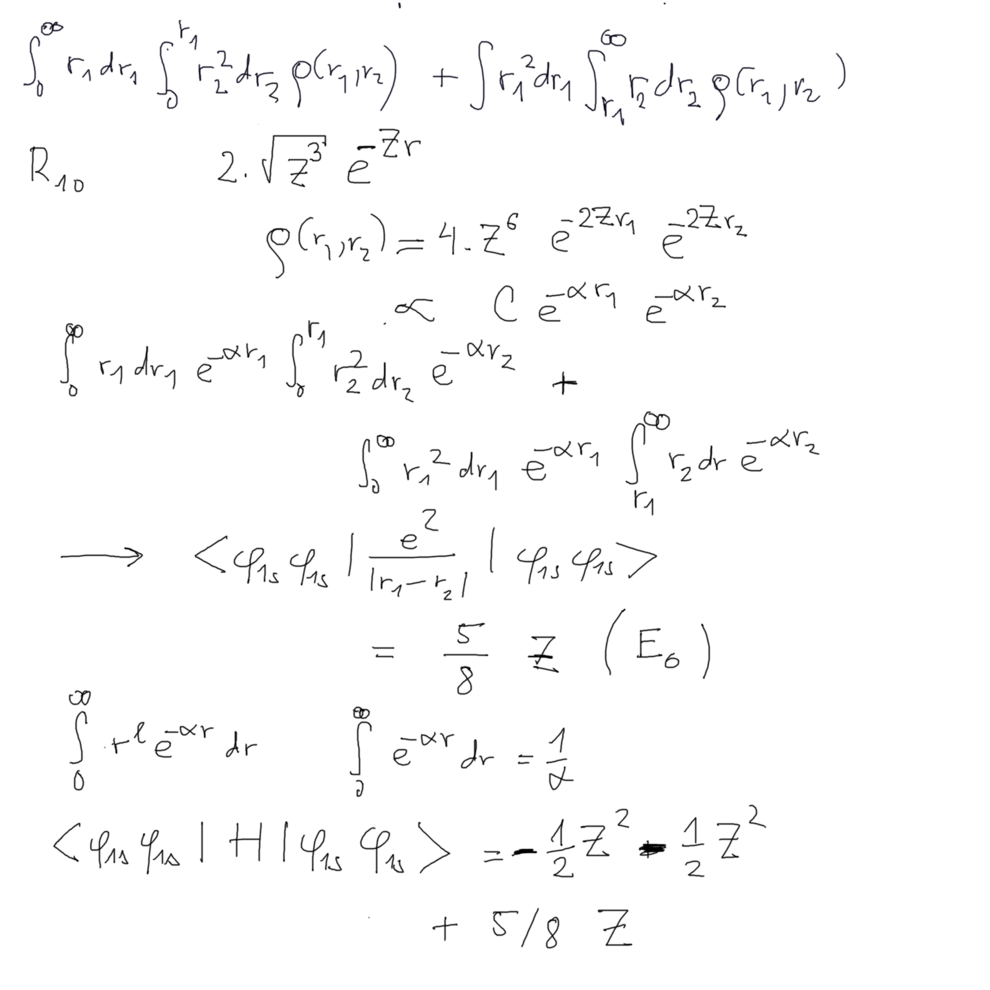
xcf_0060.png
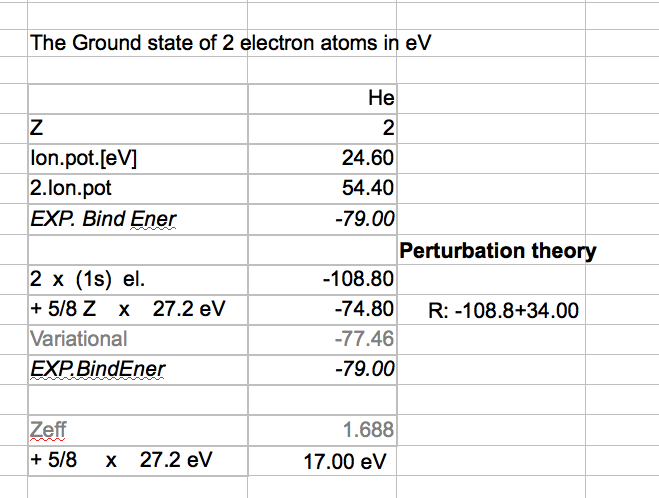
Last time we already made a comparison - here is the table again - with additional details
A000-spreadsheet-energies.png
A000-spreadsheet-energies.png |
See the detals of the terms in the summary below. Repulsion term with Z=1 would give 27.2 * 5/8 = 17 (eV) for Z=2 repulsion term is thus 34 (eV) The two 1s hydrogen-like for Z=2 108.8 = 54.4 + 54.4 54.4 = Z2 13.6 Theory - 74.8 eV Experiment - 79.0 eV |
) shows the details of the "Perturbation theory" - included above in the table

c000-product-function-perturbation.png
Below we include some details of the evaluation of the repulsion term for 1s 1s
These plates come from 2014 lecture note

g030-radial-integration-steps.png

g040-double-integral-two-parts.png
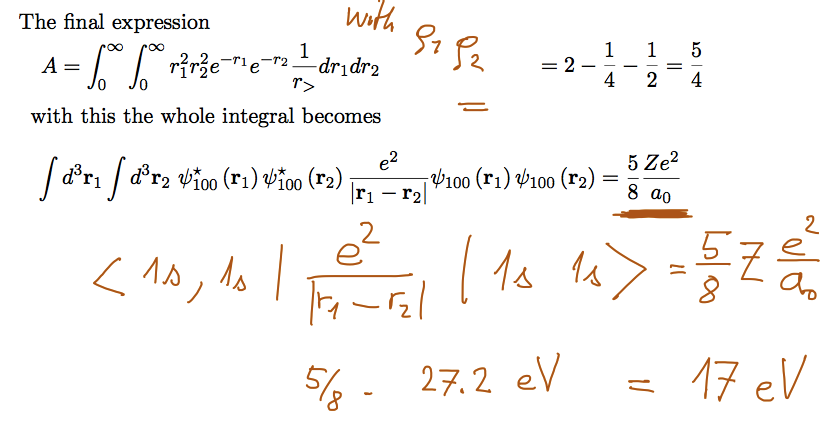
g050-expansion_evaluated_to_17_Z_eV.png
There would be possibly several L M terms and also the radial functions consist of more terms, higher power of r
NEXT TIME - GROUND STATE final approach - variational method; Configuration mixing (short)
and EXCITED STATES the role of spin - para and orthohelium
See also the PDF-note He_and_2-el_atoms.pdf
Consult also the last year's lecture note 2014_09_18/index.html for variational method
and 2014_09_02/index.html note for spin discussion