Helium and 2-2lectron atoms (ions)
Variational, Configuration Mixing, etc
First one theorem: expectation value of H in any state is always larger
than the Ground State energy
This is used in many variational calculations
Make the state depend on a variable ... e.g. z, then H(z) must have a
minimum (can not go under E_gs )
xcf_a010.png

xcf_a010.png
Variational model for our Helium
treatment
The perturbation expression with repulsion evaluated to 5/8
Z (previous lectures)
Assume that while nucleus has charge Z, the electrons can feel (an
effective) charge z
(shielding, screening of the nuclear charge by the other electron)
xcf_a020.png

xcf_a020.png
RESULT OF THE VARIATIONAL METHOD
z = Z - 5/16 i.e.
roughly z = Z - 0.3
See the table
Table_eV_binding_energies.png
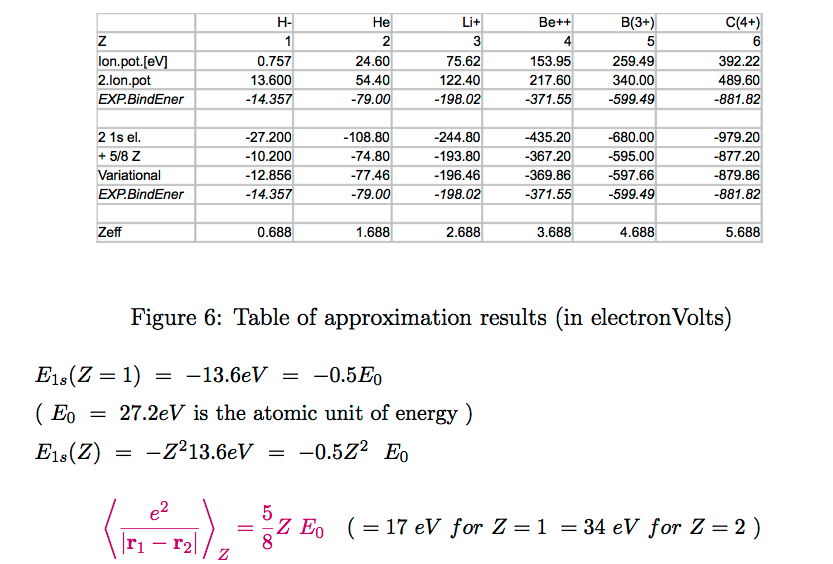
Table_eV_binding_energies.png
Here the variational method is summarized,
and we explore the "missing correlation" energy (note the about
1.5 eV for all listed Z)
OUTLINE Hyleraas 1929 work - variational method with correlated
function - what is correlated ?
xcf_a030.png

xcf_a030.png
Alternative description of correlations: CONFIGURATION MIXING
xcf_a040.png

xcf_a040.png
Exchange energy
Alternative
explanation
of the triplet - singlet energy difference
THIS
WILL
BE GENERALIZED to 3 and
many particles
xcf_a045.png
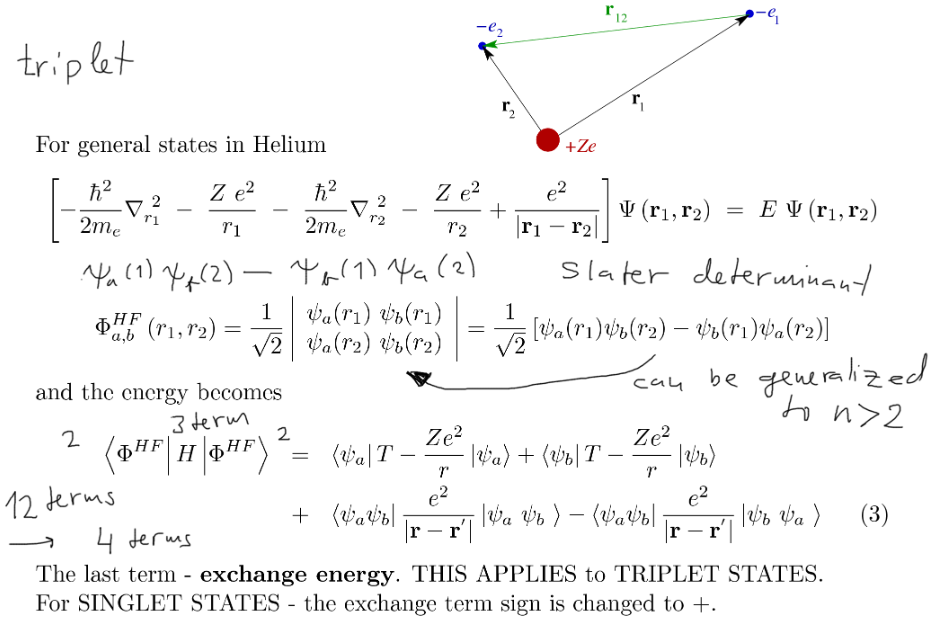
xcf_a045.png
How does it go - the
2
times 3 times 2 = 12 terms become just 4
terms !
Look here - we did it at the
whiteboard:
xcf_a050.png

xcf_a050.png
Doubly excited
states in Helium
Autoionization
The same energy as free electron
Bound only for some time
- lifetime - Decay Decaying states
x_100_doubly-excited.png
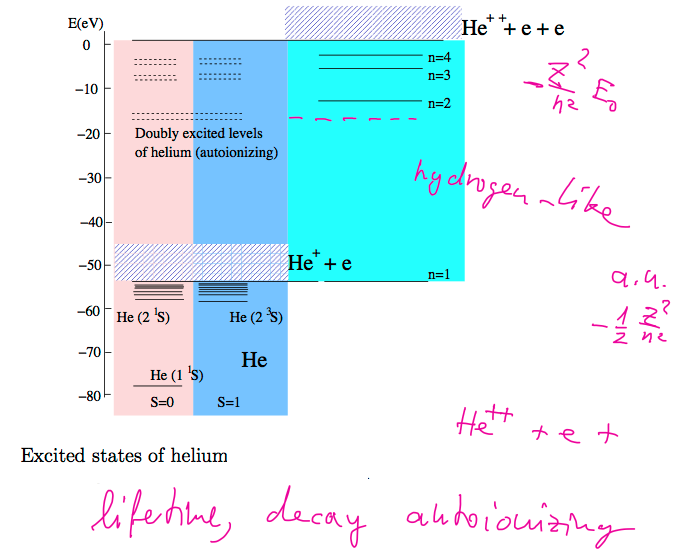
x_100_doubly-excited.png
x_200_doubly-excited.png

x_200_doubly-excited.png








