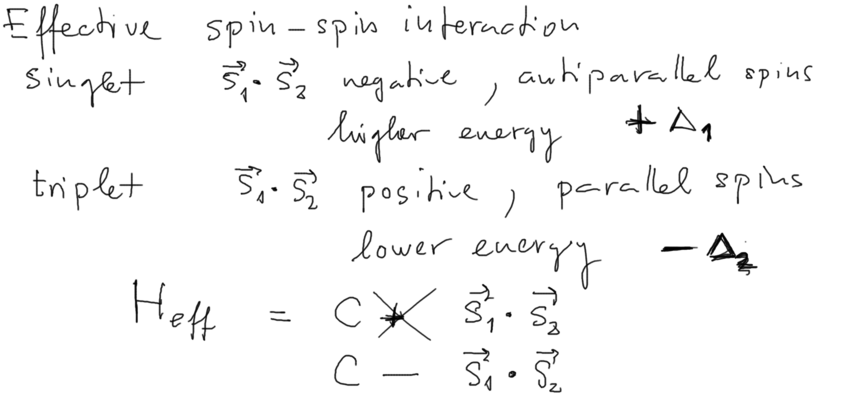Helium - Parahelium and
Orthohelium - Spin Angular Momentum
Exchange interaction - Ferromagnetism
see also
../2013_09_05/index.html
(
and
to
spome
extent
also
../2013_09_10/index.html
)
and
../2012_09_20/index.html
as
well
as
../2011_09_08/index.html
(
open
the
links
in
new
tabs
/
windows
for
easier work )
In this lecture we need first to review some points on ANGULAR MOMENTUM
in quantum mechanics.
( look at http://en.wikipedia.org/wiki/Angular_momentum_operator
)
Angular momentum is well known from classical mechanical problems
We experience it in various forms also in everyday life
( a good review in http://en.wikipedia.org/wiki/Angular_momentum
)
Commutators, operators, Levi-Civita epsilon. Levi-Civita epsilon
useful for definition of VECTOR PRODUCT
http://en.wikipedia.org/wiki/Levi-Civita_symbol#Three_dimensions_2
and also other parts of the text http://en.wikipedia.org/wiki/Levi-Civita_symbol
Spin operator behaves as (is constructed to behave as) angular momentum
- in terms of commutators,
"vector product with itself"
Pauli matrices (multiplication by h-bar ! )
( this link might be useful: http://en.wikipedia.org/wiki/Spin_(physics)#Mathematical_formulation
)
xcf_010.png

xcf_010.png
Pauli matrices - Spin operators
Addition of two angular momenta - Addition of 2 SPINS
( this article is somewhat useful, in general: http://en.wikipedia.org/wiki/Angular_momentum_coupling
Another illustration at this level: http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/vecmod.html
There are many texts at more mathematical level.
Clebsch-Gordan Coefficients text http://en.wikipedia.org/wiki/Clebsch%E2%80%93Gordan_coefficients
contains useful text, unfortunately the authors have gone crazy with
mathematics
( we should know http://en.wikipedia.org/wiki/Clebsch%E2%80%93Gordan_coefficients#Tensor_product_space
but with a simpler notation usual in physics )
For 2 spins - SYMMETRIC and ANTISYMMETRIC combinations - TRIPLET and
SINGLET
xcf_020.png

xcf_020.png
Addition of two angular momenta - Addition of 2 SPINS -
TRIANGLE CONDITION
Conservation of SUM OF 2 ANGULAR MOMENTA
For 2 spins - TRIPLET and SINGLET
xcf_030.png

xcf_030.png
a0010_2_spin_antisym_singlet_sym_triplet.png

a0010_2_spin_antisym_singlet_sym_triplet.png
a0020_singlet_triplet_-2-SPIN.png

a0020_singlet_triplet_-2-SPIN.png
a0030_orthohelium_triplet_lower_energy.png

a0030_orthohelium_triplet_lower_energy.png
a0040_orthohelium_triplet_REPULSION_REDUCED.png

a0040_orthohelium_triplet_REPULSION_REDUCED.png
xcf_040.png
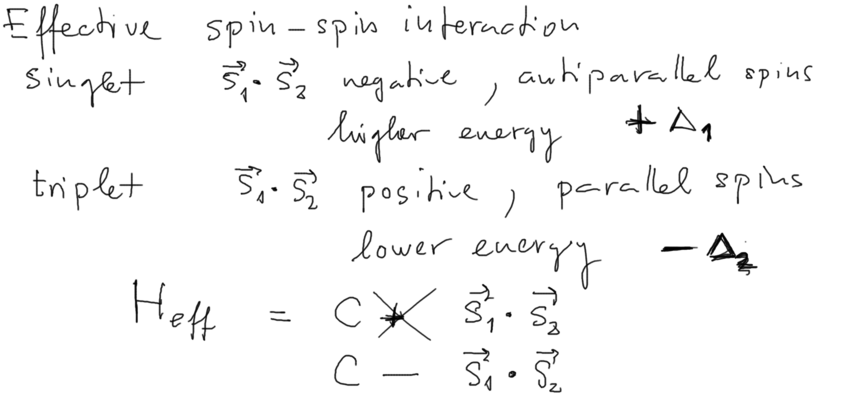
xcf_040.png
a0050_effective_symmetry_SPIN-SPIN-interaction.png

a0050_effective_symmetry_SPIN-SPIN-interaction.png
a0060_effective_symmetry_SPIN-SPIN-interaction.png

a0060_effective_symmetry_SPIN-SPIN-interaction.png
NEXT LECTURE
xcf_049.png

xcf_049.png