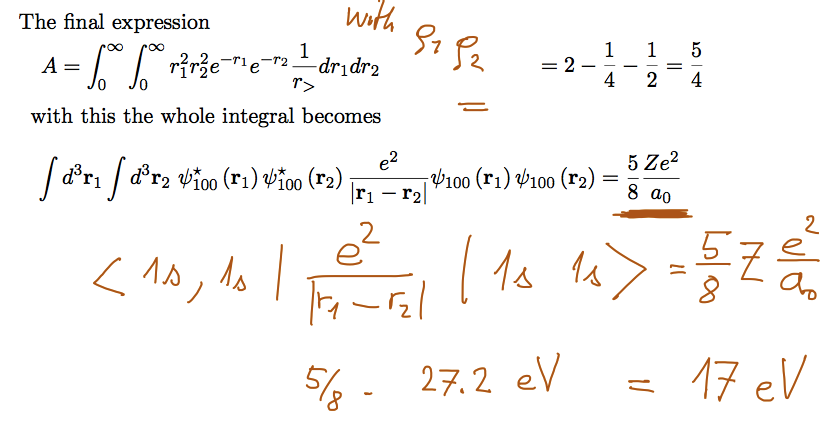Helium - 28.08.2014
1. Evaluation of repulsion; Perturbation Theory; Multipole expansion
2. Pauli principle and Spin - Parahelium, Orthohelium
1. Evaluation of repulsion;
Perturbation Theory; Multipole expansion
We start by mentioning the Fine structure constant - supplements atomic
units;
It does express the "weakness" of electro(magnetic) interactions
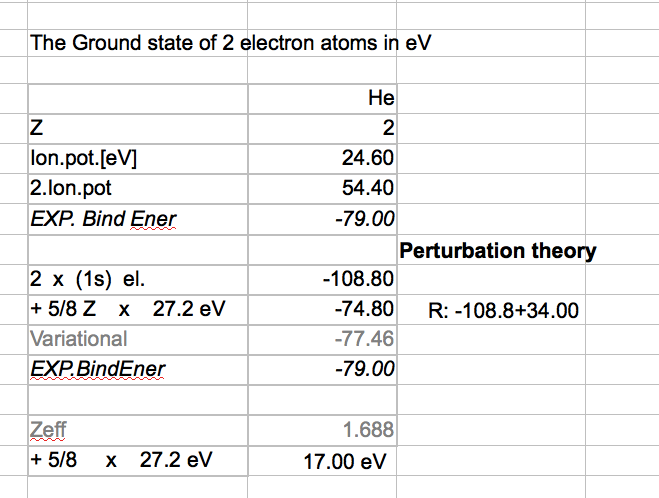
Then we start looking at the numerical values from the last lecture -
starting the perturbation theory
At the bottom of the frame - the spreadsheet of the numbers (this is
expanded below)
xcf_a010.png

xcf_a010.png
Independent electrons with
neglected repulsion give
4*13.6*2 = 108.8 eV for the total binding of the
two electrons.
Further we shall look how the repulsion can be evaluated
c000-product-function-perturbation.png

c000-product-function-perturbation.png
Spreadsheet,
includes the above reported repulsion
contribution 5/8*27.2*Z eV
The variational method will be discussed in the next lectures
A000-spreadsheet-energies.png
A000-spreadsheet-energies.png
Perturbation theory
from astronomy, applied mathematics - http://en.wikipedia.org/wiki/Perturbation_theory-
see
also
http://en.wikipedia.org/wiki/Perturbation_theory_(quantum_mechanics)
in particular (as sketched below)
http://en.wikipedia.org/wiki/Perturbation_theory_(quantum_mechanics)#First_order_corrections
(Note that the word "perturbation" is somewhat special; outside of
mathematical sciences
"perturbed"
means "thrown into a
state of agitated confusion" or
"worried or upset by something"
xcf_a020.png

xcf_a020.png
The energy correction
(1. order)
is the same number as the EXPECTATION VALUE of the perturbation term
In 2-electron system (He and related IONS) this expectation value is a
6-dimensional integral
Here we sketch the evaluation, below we go shortly through the details
xcf_a030.png

xcf_a030.png
How to evaluate the EXPECTATION VALUE of the perturbation term - the electron-electron
repulsion
In 2-electron system (He and related IONS) this expectation
value is a 6-dimensional integral
g010_Repulsion_term.png

g010_Repulsion_term.png
General method - valid for any pair of "orbitals" (the
electronic states are often called orbitals)
Multipole expansion, spherical harmonics.
An integral over any spherical harmonics (except of 00 ) over the
sphere surface (4 pi) is allways ZERO
This follows from orthonormalization, for example
g020_repulsion_6dim_to_double_radial.png

g020_repulsion_6dim_to_double_radial.png
So this reduces to a double radial integration, and the radial 1s
functions have a simple form.
The integrals of powers with exponentials are rather easily evaluated
g030-radial-integration-steps.png

g030-radial-integration-steps.png
Here we reproduce overview of the steps - dividing the integral into 2
terms according to what r< and r>
mean in different integration regions
g040-double-integral-two-parts.png

g040-double-integral-two-parts.png
The result has already been used above.
Note that the same approach can be used for ANY PAIR OF HYDROGEN-like
ORBITALS
g050-expansion_evaluated_to_17_Z_eV.png
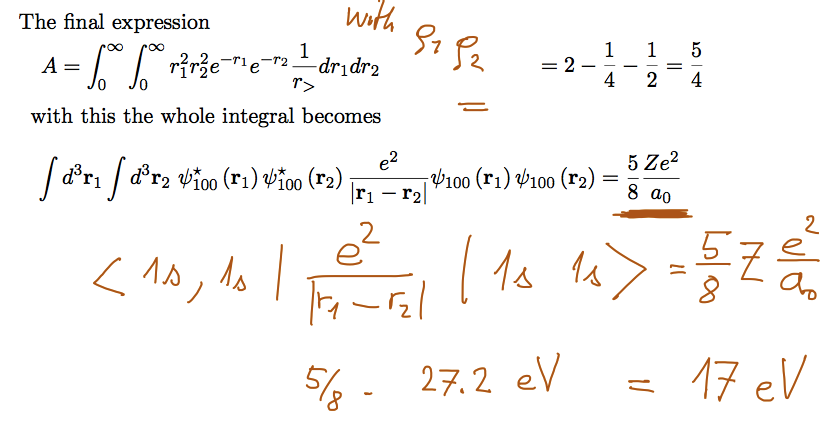
g050-expansion_evaluated_to_17_Z_eV.png
2. Pauli principle and Spin -
Parahelium and Orthohelium
c010-para-ortho.png

c010-para-ortho.png
Spectra of PARA and ORTHOHELIUM
c020-levels-para-ortho.png
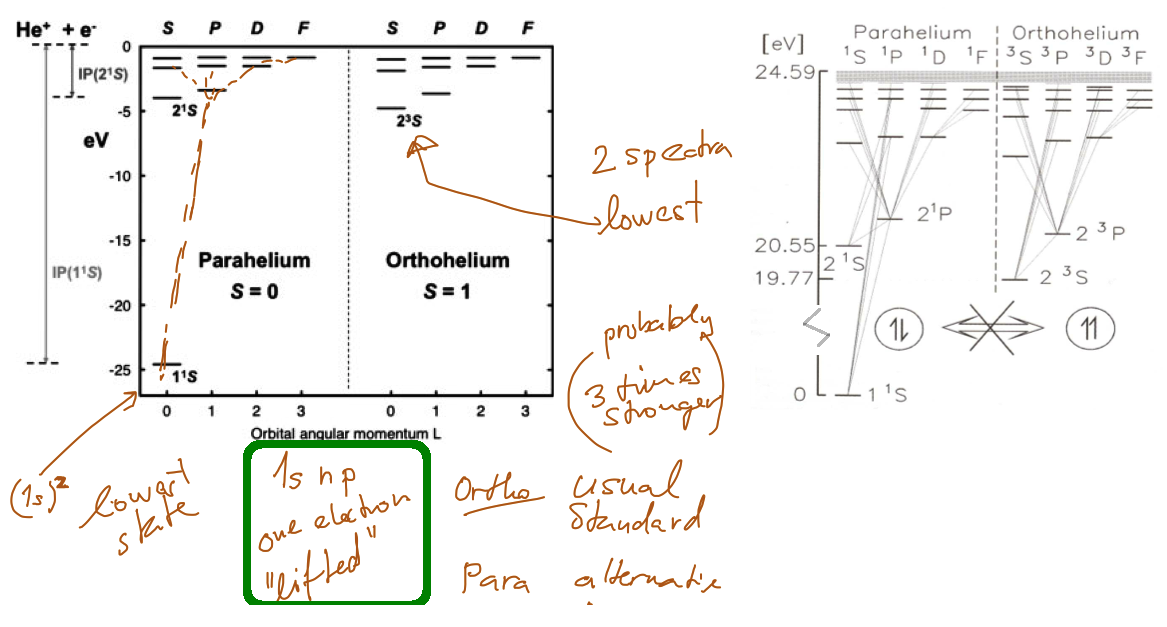
c020-levels-para-ortho.png
Spectra of PARA and
ORTHOHELIUM -detail
c030-levels-para-ortho-large.png
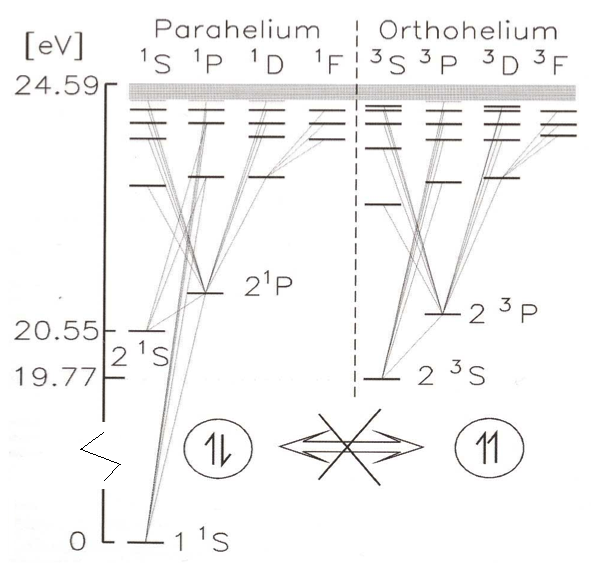
c030-levels-para-ortho-large.png
Exclusion principle
- justified by the "identical particle exchange independence"
Currently most known as exchange
symmetry
xcf_a040.png

xcf_a040.png
xcf_a050.png

xcf_a050.png
xcf_a060.png

xcf_a060.png
c040-Pauli-exclusion-exchange.png

c040-Pauli-exclusion-exchange.png
c050-antisymmetry_PRODUCT_independent.png

c050-antisymmetry_PRODUCT_independent.png
c060-antisymmetry_j-j-coupling.png

c060-antisymmetry_j-j-coupling.png
Next part:
functions for two spins; origin of spin; singlet og triplet spin states