Hydrogen-like atoms - last
part; Starting Helium
First we look back at the quantum mechanics courses,
hydrogen atom etc.
What determines the bound states? The probability density - square of
the wave function.
That gives the normalization.
But it also requires that the integral over the whole space exists.
Solutions of the (partial) differential equation for general energy
value run to infinity. Only in some few cases
they tend to zero for "outside" regions. Those energies are then the
physical solutions.
Important to remember the 1s (l=0) state (ground state) shape:
simple exponential.
How do the other states behave? ---- We discuss the radial functions
for l > 0
They have a "hole" close to the nucleus. ( r to the power of l
when r close to zero )
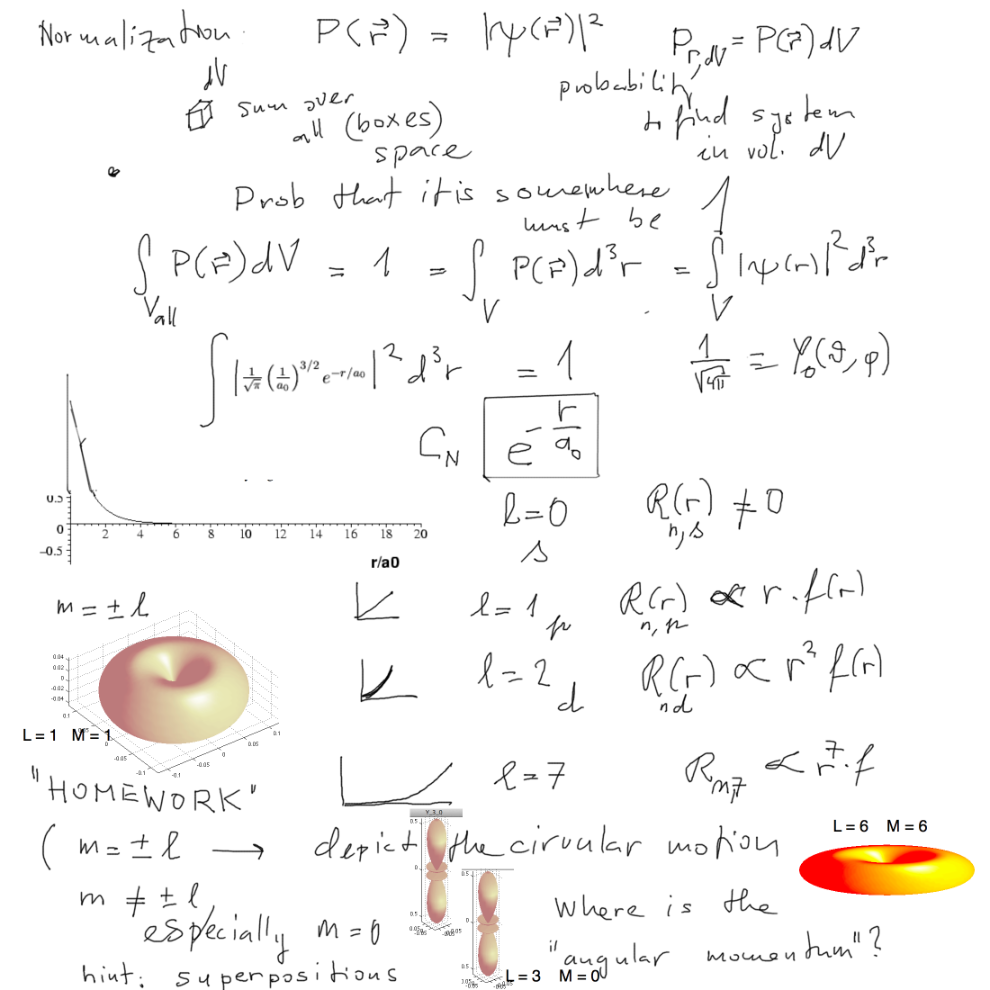 0010.png
0010.png
Here we formulated a "homework" - above
For M=L - circular - the angular function is limited to directions
close to x,y plane
(plotted is the Y_LM abs. value squared as function of theta and phi)
So the "doughnut" shape is considtend with the classical idea - but
where is the motion?
Question 1: where is the circular motion? Hint:
remember the probability density current?
provided you answered question 1 -
Question 2: O.K., but where is the motion in e.g. L=6, M=0 ( see
below)
Here is a collection of some other polar plots, but here we show
the circular states (maximum m=l )
and
compare
with
some
small m and m=0 states
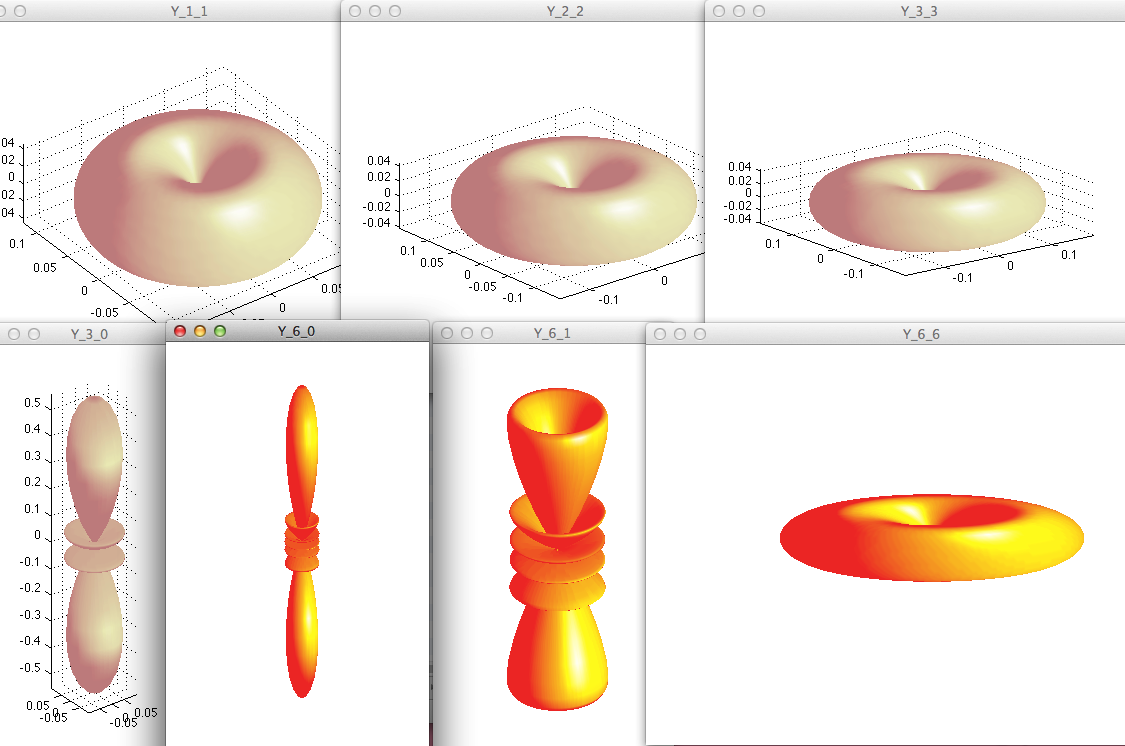 0012_Matlab-Doughnut_M-equal_L-rotation.png
0012_Matlab-Doughnut_M-equal_L-rotation.png
Atomic units (
see
also
the
end
of the Helium text He_and_2-el_atoms_2013.12.04.pdf)
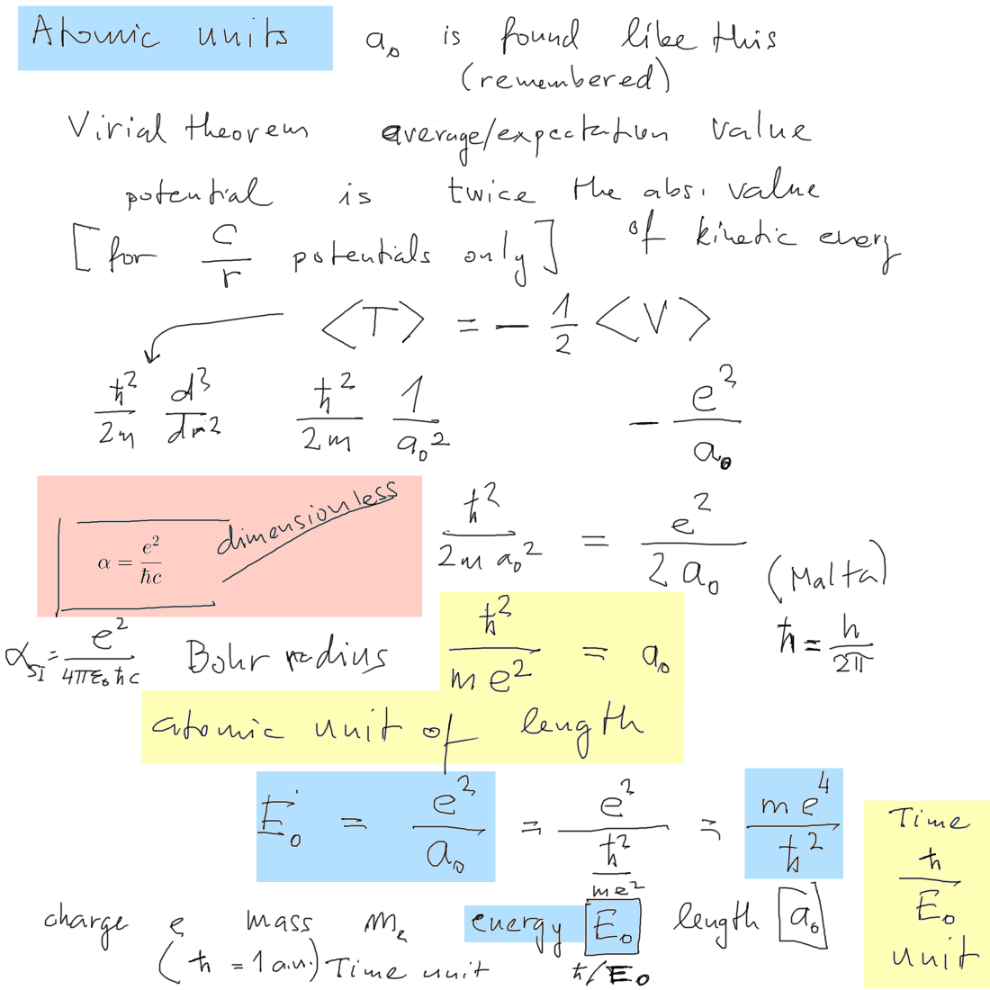 0020.png
0020.png
BELOW we also discuss the SI units ( MKSA - 4 fundamental units -
and rationalized - 4 pi )
compared to Gaussian approach ( cgs - 3 fundamental units and no
adjusting of 4 pi )
The atomic units follow the Gaussian approach, the three fixed values
are LENGTH (Bohr radius) ENERGY (27.2 eV = 2 x 13.6 eV)
and ENERGY x TIME - the hbar is the unit, giving the unit of TIME as
hbar / 27.2 eV
The more precise value of the energy
unit
is 27.21138505 eV
( see also the end of the Helium text He_and_2-el_atoms_2013.12.04.pdf)
 atomic_units.png
atomic_units.png
The more precise value of the energy
unit
is 27.21138505 eV
HERE we discuss the SI units ( MKSA - 4 fundamental units -
and rationalized - 4 pi )
compared to Gaussian approach ( cgs - 3 fundamental units and no
adjusting of 4 pi )
The atomic units follow the Gaussian approach, the three fixed values
are LENGTH (Bohr radius) ENERGY (27.2 eV = 2 x 13.6 eV)
and ENERGY x TIME - the hbar is the unit, giving the unit of TIME as
hbar / 27.2 eV
 0035.png
0035.png
Above it says ( elementary charge - i.e. minus electron charge ) is
the unit of charge.
Not really! We do not need a "unit" - it is determined by the unit
potential energy - so two charge have
a potential energy of 1 a.u. at distance 1 a.u. of length - then they
can be used as a unit of "charge"
The spectrum of hydrogen
(from http://physics.unm.edu/Courses/Finley/p262/Hydrogen/WaveFcns.html
)
with a discussion and a mention of SELECTION RULES
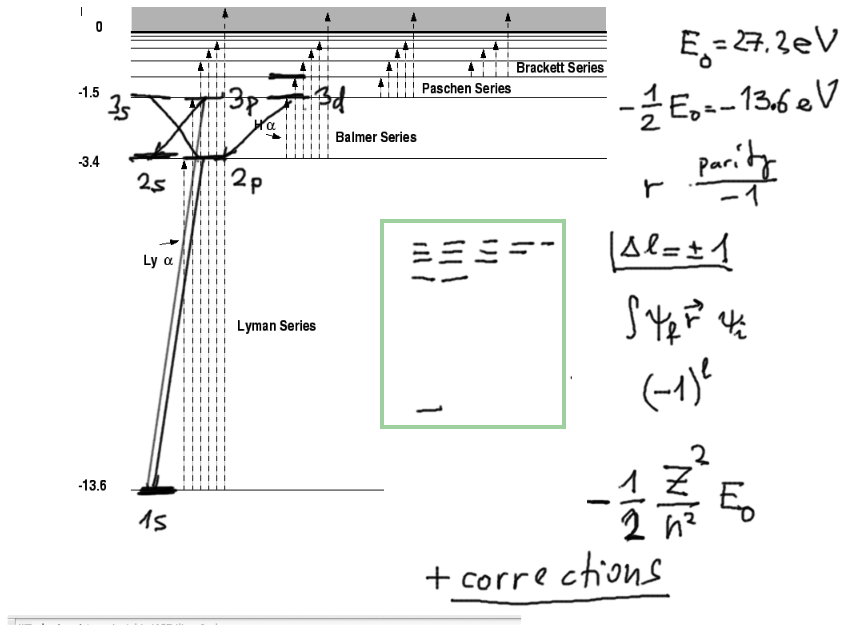 0031.png
0031.png
About corrections to Energy
Level and lines diagram from http://physics.nist.gov/PhysRefData/ASD/lines_form.html
This diagram requires Java in the browser, at present de-popularized
due to possible security problems
when used on untrusted sites ( we can trust NIST - http://www.nist.gov)
The atomic database: http://www.nist.gov/pml/data/asd.cfm
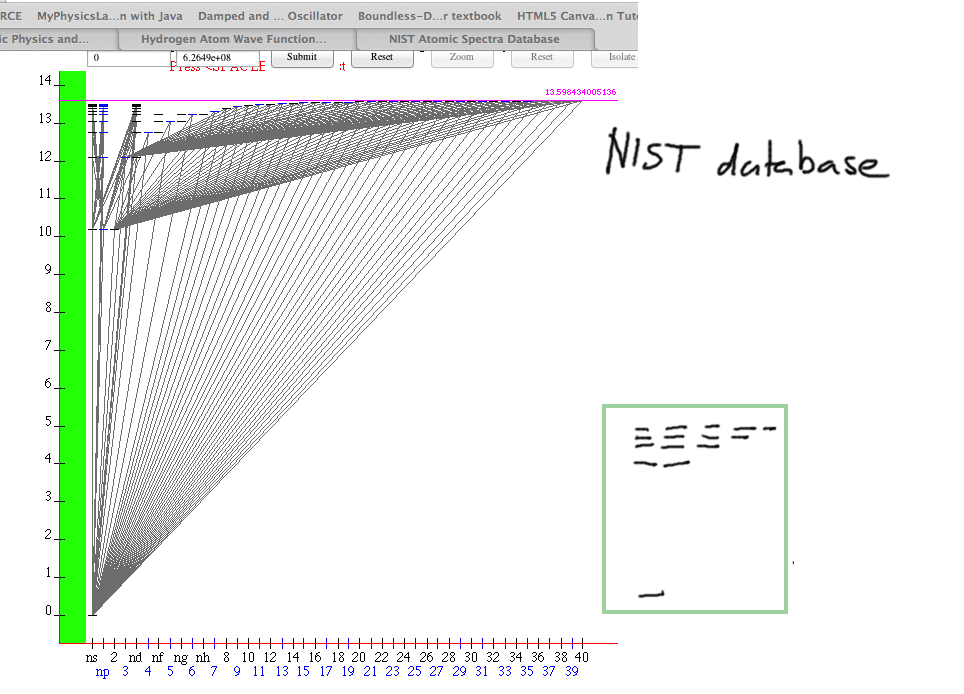 0032.png
0032.png
Helium and
2-electron atoms
starting with the hydrogen-like system - the Helium ion
Helium ion spectrum at http://physics.nist.gov/PhysRefData/ASD/lines_form.html
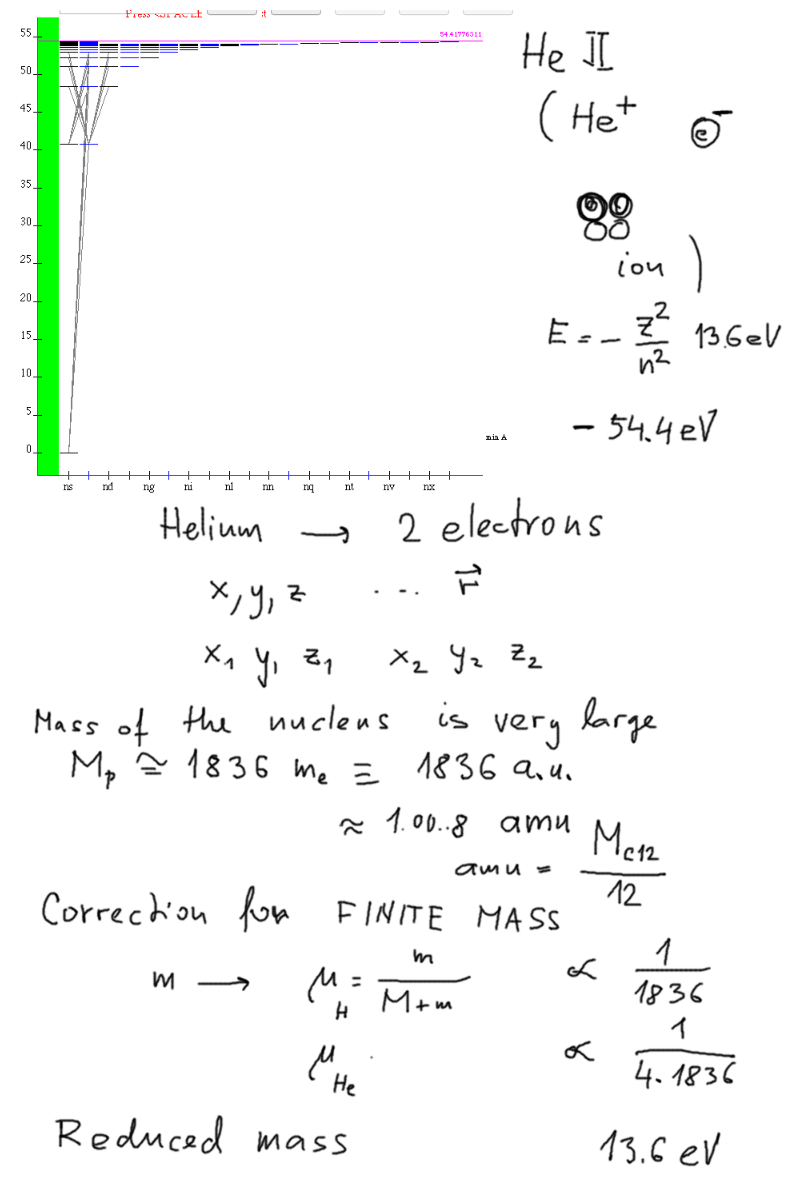 0040.png
0040.png
NOTE THE BOUND STATE OF He+ - - 54.4
eV
Helium and 2-electron
atoms
Using the slides in He_and_2-el_atoms_2013.12.04.pdf
Helium isoelectronic sequence - some examples mentioned
 0053.png
0053.png
 0054.png
0054.png
 0055.png
0055.png
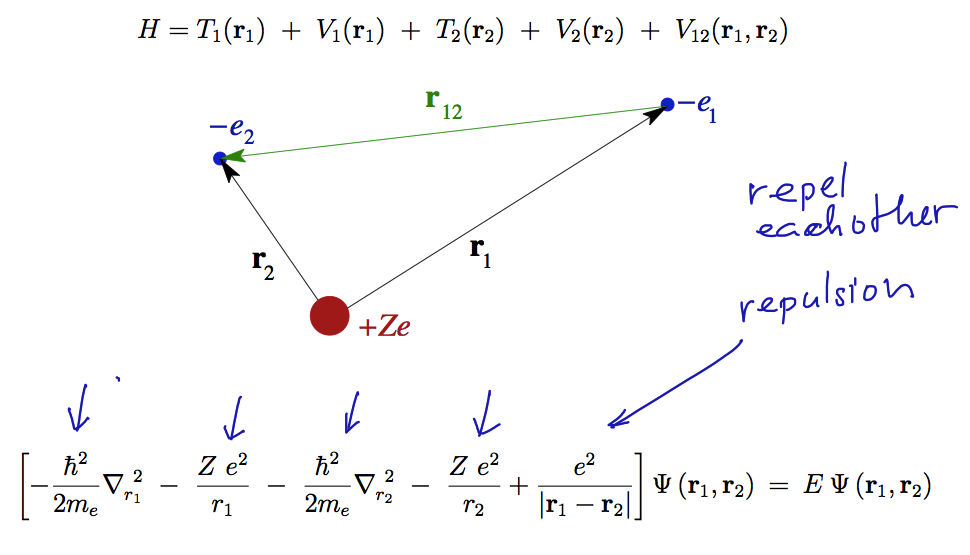
We continue to the
hydrogen-like based simple picture of helium, neglecting the repulsion
 0058.png
0058.png
We continue to the hydrogen-like based simple picture of helium,
neglecting the repulsion
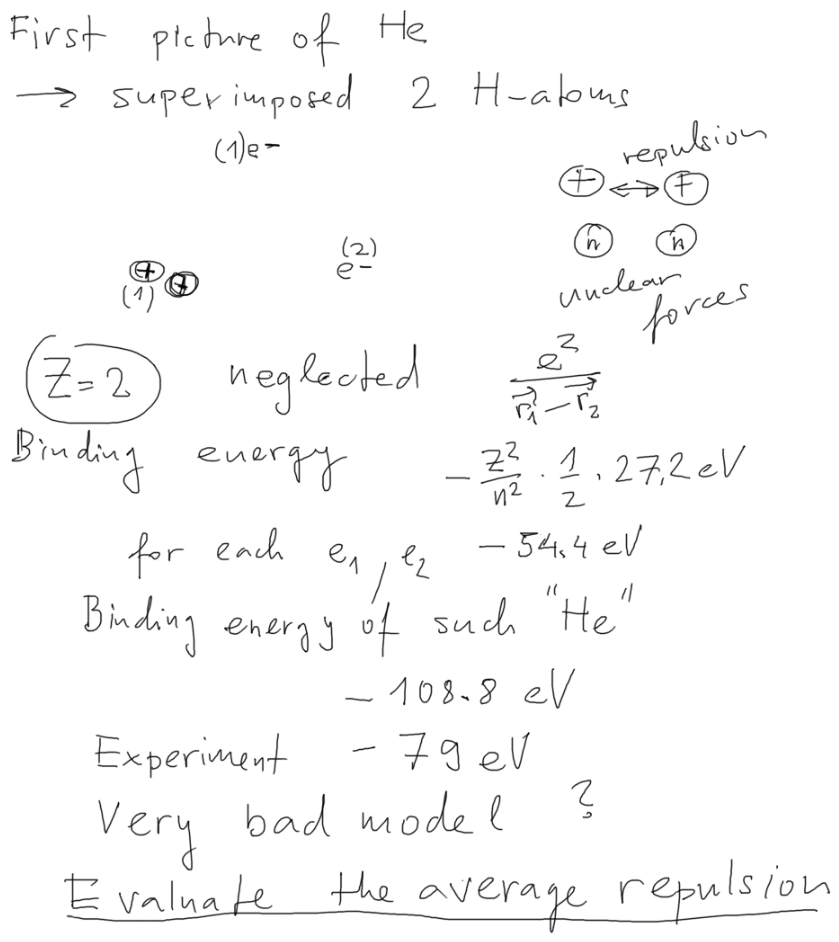 0059.png
0059.png
Next time we will continue to the hydrogen-like based simple
picture of helium, including the
repulsion
It can be
called
Perturbation theory
 0062.png
0062.png
 0010.png
0010.png  0012_Matlab-Doughnut_M-equal_L-rotation.png
0012_Matlab-Doughnut_M-equal_L-rotation.png  0020.png
0020.png  atomic_units.png
atomic_units.png  0035.png
0035.png  0031.png
0031.png  0032.png
0032.png  0040.png
0040.png  0053.png
0053.png  0054.png
0054.png  0055.png
0055.png  0058.png
0058.png  0059.png
0059.png  0062.png
0062.png