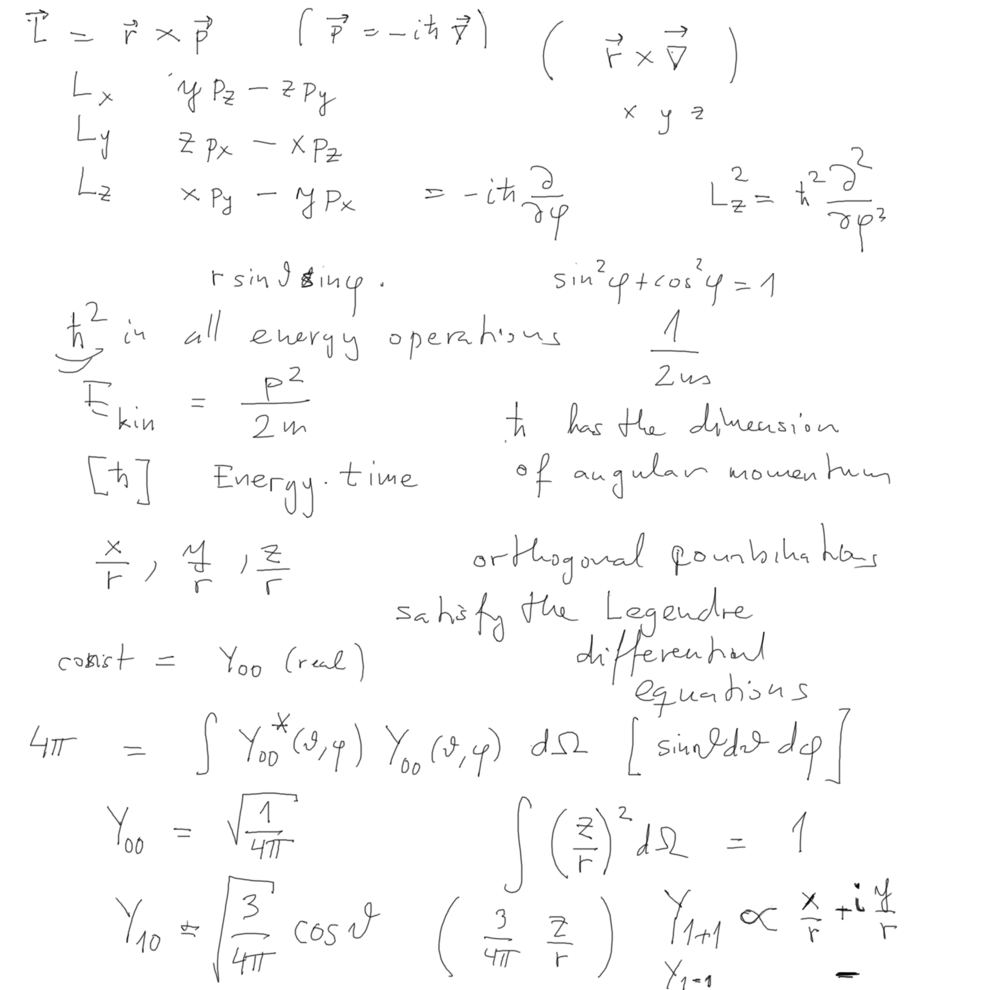PHYS261 - Atomic Physics and Physical Optics

to index 2014.08.19 Previous Lecture Note LECTURE NOTE 2014.08.21 2014.08.26 next lecture note

Basic Knowledge - Hydrogen Atom

Here we continue the introduction, mainly directed to basic knowledge
about the hydrogen-like atomic systems.

Extra pages on graphics Graphical study of Hydrogen Bound States (MATLAB)

These are mentioned in most introductory courses of Modern Physics, Quantum mechanics etc
Those are:
     Schrödinger equation for Coulomb potential
     Separation of radial and angular parts; Spherical harmonics
     Eigenvalues; Bound states of hydrogen
     Energy levels; Spectra of hydrogen
     Selection rules

Most of these basic topics are covered for example in these
LINKS:
Hydrogen atom wavefunctions http://en.wikipedia.org/wiki/Hydrogen_atom#Wavefunction
Laplace operator http://en.wikipedia.org/wiki/Laplace_operator#Three_dimensions
Legendre Polynomials http://en.wikipedia.org/wiki/Legendre_polynomials
Spherical harmonics http://en.wikipedia.org/wiki/Spherical_harmonics
Table of them http://en.wikipedia.org/wiki/Table_of_spherical_harmonics

List of Radial functions: http://en.citizendium.org/wiki/hydrogen-like_atom#List_of_radial_functions
see also the whole article http://en.citizendium.org/wiki/hydrogen-like_atom - better than wikipedia

Schrödinger equation for radial potential (central potential, spherically symmetric, isotropic .......)
and thus for the point charge Coulomb potential.
Separation of Variables, Radial and Angular; Angular Momentum operator - see also below
xcf_b011.png

xcf_b011.png
Separation r and angles; Further separation - theta and phi;
For phi - instead of boundary condition - the periodicity over 360 degrees is used

Angular Momentum operator (Squared L) - Angular part -> Legendre Polynomials http://en.wikipedia.org/wiki/Legendre_polynomials
xcf_b020.png

xcf_b020.png

Angular Momentum operator --> angular variables only - see the dimensional analysis
Angular Momentum has the dimension of Action - Planck's constant.
Angular momentum quantized - in units of h-bar
xcf_b030.png

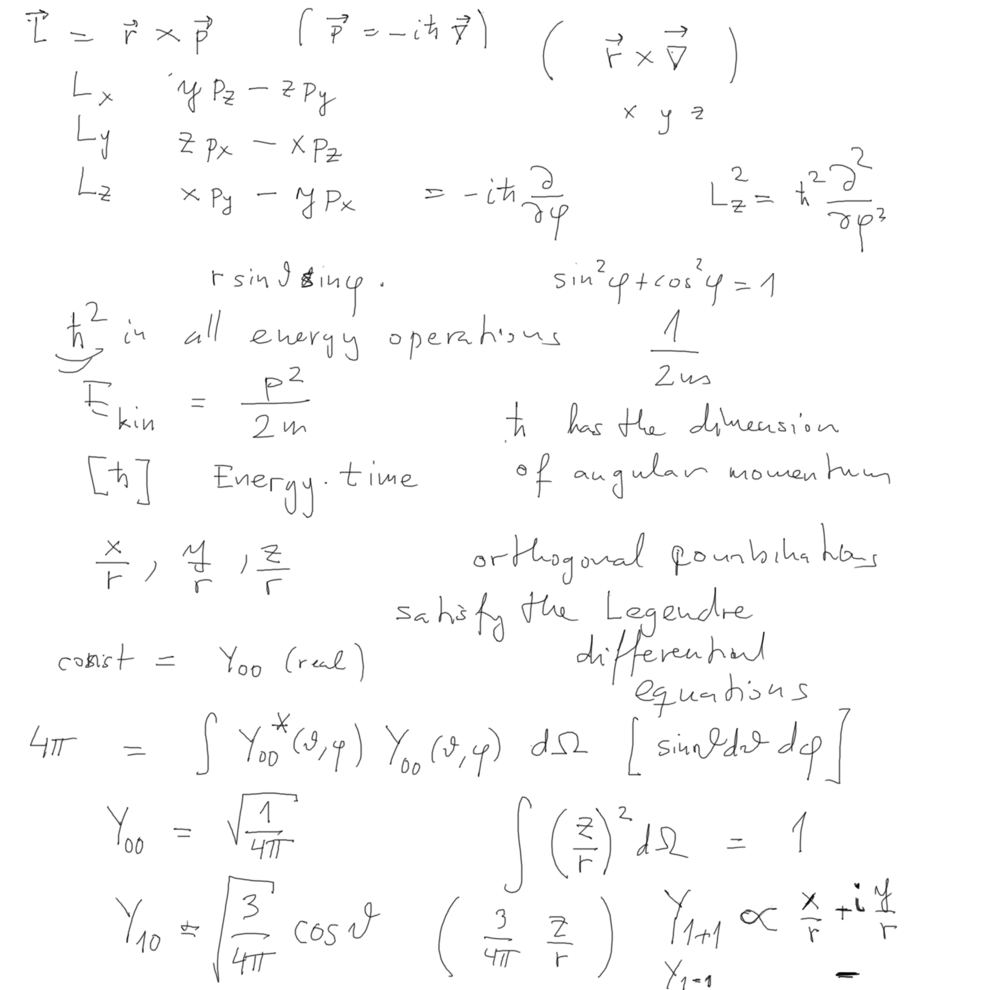
xcf_b030.png

Spherical harmonics are (also) orthogonalized polynomials of x/r y/r and z/r - see above

Spherical harmonics, polar plots, Popular Culture, Wikipedia
Note: wikipedia has chemistry - prefered REAL-valued spherical harmonics as illustrations

xcf_b040.png

xcf_b040.png
See the complex valued Ylm - extra pages on graphics Graphical study of Hydrogen Bound States (MATLAB)

xcf_b050.png

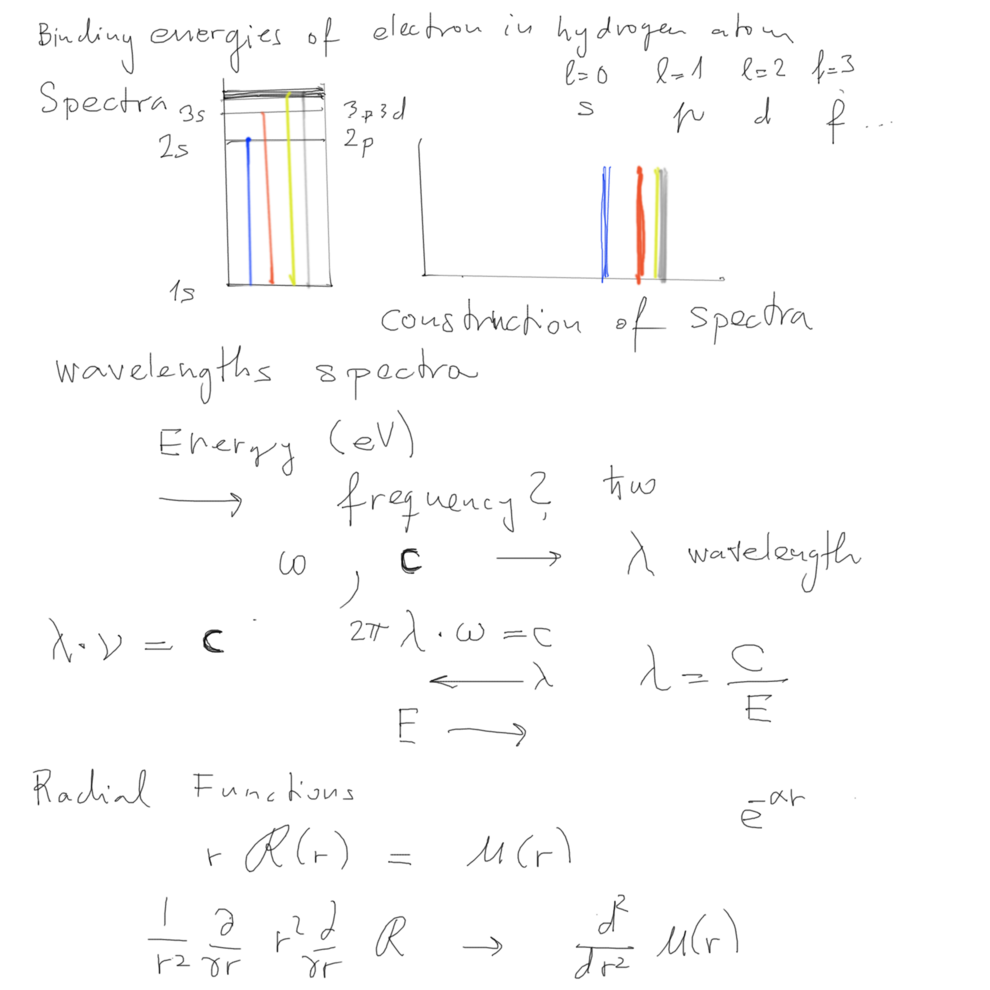
Solutions are called Laguerre Polynomials multiplied by exponential

List of Radial functions: http://en.citizendium.org/wiki/hydrogen-like_atom#List_of_radial_functions
see also the whole article http://en.citizendium.org/wiki/hydrogen-like_atom - better than wikipedia

Energies: 13.6( Z2 / n2 ) eV (electronVolts)

Ask Google: 1 electron volt = 1.60217657 × 10^-19 joules

Build energy levels - combine to spectra
Relation of wavelengths - energies
xcf_b060.png

xcf_b060.png

Psi_hydrogen_citizendum.png

Relation of wavelengths - energies - program lines for Octave or MATLAB

energ_eV  = 1238.6 / lambda_nm

200.00 nm         6.19 eV
    225.00 nm         5.50 eV
    250.00 nm         4.95 eV
    275.00 nm         4.50 eV
    300.00 nm         4.13 eV
    325.00 nm         3.81 eV
    350.00 nm         3.54 eV
    375.00 nm         3.30 eV
    400.00 nm         3.10 eV
    425.00 nm         2.91 eV
    450.00 nm         2.75 eV
    475.00 nm         2.61 eV
    500.00 nm         2.48 eV
    525.00 nm         2.36 eV
    550.00 nm         2.25 eV
    575.00 nm         2.15 eV
    600.00 nm         2.06 eV
    625.00 nm         1.98 eV
    650.00 nm         1.91 eV
    675.00 nm         1.83 eV
    700.00 nm         1.77 eV
    725.00 nm         1.71 eV
    750.00 nm         1.65 eV
    775.00 nm         1.60 eV
    800.00 nm         1.55 eV
    825.00 nm         1.50 eV
    850.00 nm         1.46 eV
    875.00 nm         1.42 eV
    900.00 nm         1.38 eV
    925.00 nm         1.34 eV
    950.00 nm         1.30 eV
    975.00 nm         1.27 eV
   1000.00 nm         1.24 eV

lambda_nm = 1238.6 / energ_eV

1.00 eV      1238.60 nm
      1.10 eV      1126.00 nm
      1.20 eV      1032.17 nm
      1.30 eV       952.77 nm
      1.40 eV       884.71 nm
      1.50 eV       825.73 nm
      1.60 eV       774.12 nm
      1.70 eV       728.59 nm
      1.80 eV       688.11 nm
      1.90 eV       651.89 nm
      2.00 eV       619.30 nm
      2.10 eV       589.81 nm
      2.20 eV       563.00 nm
      2.30 eV       538.52 nm
      2.40 eV       516.08 nm
      2.50 eV       495.44 nm
      2.60 eV       476.38 nm
      2.70 eV       458.74 nm
      2.80 eV       442.36 nm
      2.90 eV       427.10 nm
      3.00 eV       412.87 nm
      3.10 eV       399.55 nm
      3.20 eV       387.06 nm
      3.30 eV       375.33 nm
      3.40 eV       364.29 nm
      3.50 eV       353.89 nm
      3.60 eV       344.06 nm
      3.70 eV       334.76 nm
      3.80 eV       325.95 nm
      3.90 eV       317.59 nm
      4.00 eV       309.65 nm
      4.10 eV       302.10 nm
      4.20 eV       294.90 nm
      4.30 eV       288.05 nm
      4.40 eV       281.50 nm
      4.50 eV       275.24 nm