PHYS261 - autumn 2015

to index 2015_09_02 Previous lecture note LECTURE NOTE 2015_09_16 2015_09_17 Next lecture note

Helium: Ground state - Variational Method. Excited States. Electron Spin.

In this lecture we looked at the basis for the so called Variational Method- for the GROUND STATE, based on the
extension - and reformulation - of the Perturbation theory (for repulsion) discussed before.

Then we started with treatment of EXCITED STATES (i.e. not the GROUND STATE).

Then we started with the role of ELECTRON SPIN

First - the perturbation result - for the ground state, as function of Z of the nucleus. We separate the
kinetic, potential and electron repulsion terms, showing their Z-dependence.

What is variation, Calculus of variations?
       wikipedia says: en.wikipedia.org/wiki/Calculus_of_variations
        Calculus of variations is a field of mathematical analysis that deals with maximizing or minimizing functionals.
       Functionals are mappings from a set of functions to the real numbers
                                  ( as Functions are mappings a set of numbers to numbers)

We shall se why A MINIMUM of a FUNCTIONAL is important in Quantum Physics
( but also in many other physics applications )

How to get to a 'set of functions' in our case - see bottom of the plate -
                     each electron 'sees' unknown    Screened z      instead of Z of the nucleus

0000_perturbation_Functionals_variation_from_mapping.png

End of the above plate: each electron 'sees' unknown    Screened z      instead of Z of the nucleus

Theorem     The exact solution for the GROUND STATE gives the lowest energy expectation
Proof next plate - for any system

0010_Ground_state_extremum_expectation_value_Hamiltonian.png

The above is thus the basis of the variational method:
             1. Find the set of possible solutions
             2. Find the minimum of the FUNCTIONAL ( i.e. the expectation value of the hamiltonian operator)

This function is then "closest to" the real solution

Below we thus see that the best screened z is given by   z = Z - 5/16        (   or about   z = Z - 0.3   - for all Z )
       i.e. the "best independent electron approximation"

0030_result_variational_z_from_Z_for_2-electrons.png

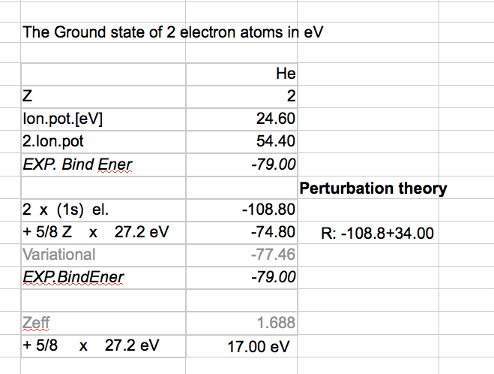
Comparison with experiment - He only

0035-spreadsheet-energies.png

Comparison with experiment - a series of Z-values for 2-electron systems

0037_TABLE_all_and_variational_six_Z_for_2-electrons.png

What to do to get electron correlations not a product - well then sum of products - configuration mixing
Configuration mixing will be visited several times later

0040_NOT-independent_correlation_Configuration_mixing.png

- or construct functions which might be good "candidates"

Functions where electrons are NOT INDEPENDENT - not a product ( Hylleraas 1930 )

en.wikipedia.org/wiki/Egil_Hylleraas

0050_Hylleraas_Variational.png

Excited states, the role of the spin
Excited states - one electron is in n,l state instead of 1s - we call this singly excited.
Also here the repulsion, configuration mixing etc will play a certain role
- but we look mainly at the role of exclusion principle (Pauli) - spin has "two possible eigenstates"

What is spin? Not really "angular momentum"
Postulated by Pauli and contemporaries; Derived from Dirac equation - it is mainly an extra (internal)

magnetic moment

0060_Helium_excited_states___Aufbau__Angular_momentum_Spin.png

Angular momentum operator - comes into the kinetic energy naturally
Commutation rules - spin operator was found to obey the same rules - Pauli matrices
Comment: we have forgotten to look into Pauli Matrices here - it will be visited later

"Exchange symmetry" - permutations and all that mentioned - next time

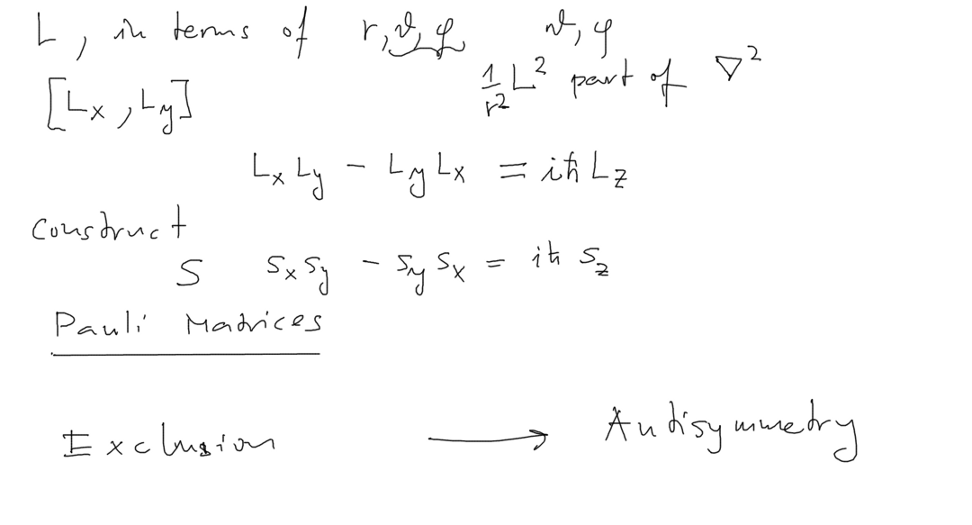
0070_Angular_momentum_Spin_exclusion_principle.png

"Exchange symmetry" - permutations and all that mentioned - next time