PHYS261 - autumn 2015

to index 2015_09_16 Previous lecture note LECTURE NOTE 2015_09_17 2015_10_07 Next lecture note

Helium and 2 electron atomic systems: more on spin. Orthohelium, Parahelium.
Doubly excited states. Configuration Mixing - from the expansion theorems.

First we revisited the magnetic moment - angular momentum - and spin relations.

And addition of angular momentum mechanisms

Two types of helium spectra - Orthohelium, Parahelium. The origin of the energy differences

Doubly excited states of Helium (this will not be of interest for other 2-electron systems - why? )

Configuration Mixing - from the expansion theorems.

Angular momentum - Magnetic Moment g=1 for L to M g=2 for s to m ( spin )
en.wikipedia.org/wiki/Magnetic_moment Long article on magnetic moment, definition etc
en.wikipedia.org/wiki/Magnetic_moment#Magnetic_moment_and_angular_momentum
en.wikipedia.org/wiki/Magnetic_moment#Magnetic_moment_of_an_electron

xcf_0000_Magnetic_Moment.png

Above, bottom: 2 electrons product wavefunction including spin description
( the spin 'wavefunction' is not really a function as e.g. 1s state radial; for us it can be a 2x1 (column) matrix )

Next plate: We find many illustrations of addition of angular momenta - from 'sort of everyday life'

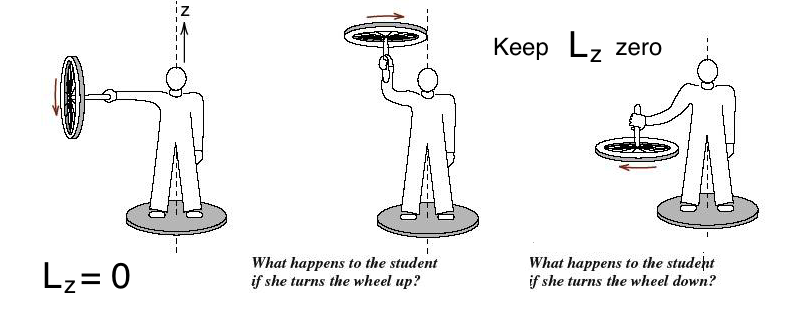
xcf_0005_addition_angular_momentum.png

Addition of angular momenta - see the trianle rule below

Pauli Exclusion Principle -- and Exchange symmetry - Identical Particles
the Aufbau Principle --> Exclusion Principle   (Build-up Principle)
                                            Exclusion Principle    justified by Fermi Statistics
                                                                                 identical particles --> Invariance for exchange of particles
the exchange of positions must not change the PROBABILITY DENSITY    ; phase      --> plus / minus 1

Antisymmetry - the    minus 1 possibility    --> leads to exclusion principle
                                                                                                   exclusion principle TRUE IF electrons are Fermions

xcf_0010_exclusion_principle.png

Above:    the exchange of positions must not change the PROBABILITY DENSITY
Below:
           But we must include both spin and space!
                                And spin and space must be INDEPENDENT
                                                                                   INDEPENDENT --->    PRODUCT wavefunctions

xcf_0020_Fermi_Bose_identical_particles_exchange_symmetry.png

Space SYMMETRIC      spin ANTISYMMETRIC
Space ANTISYMMETRIC        spin SYMMETRIC

L-S coupling        vs     j-j coupling

xcf_0030_Exchange_Symmetry_L-S-j-j-couplimgs.png

Above: spectroscopic notation
Below: towards the explanation of the ORTHOHELIUM - PARAHELIUM energy difference

xcf_0035_Triplet_SInglet_SYM_ANTISYM.png

Overview of the "symmetry properties" i.e. how must the states be combined

xcf_0039.png

ORTHOHELIUM - PARAHELIUM difference in energy explained

xcf_0040_Triplet_SInglet_SYM_S-1_ANTISYM_S_0.png

Two spin states explained singlet S=0 ( 2 S + 1 = 1 ) triplet S=1 ( 2 S + 1 = 3 )

xcf_0041.png

ORTHOHELIUM -     PARAHELIUM    difference in energy explained
triplet S=1     (SYM)    singlet S=0       (ANTISYM )
space    ANTISYM              space SYM
repulsion     reduced, small       repulsion LARGE
                                                                                          ORTHOHELIUM below     PARAHELIUM

xcf_0043_Symmetric_Antisymmetric_Spectra.png

Ground state and singly excited states - the Configurations

xcf_0100_Doubly_excited_States.png

Doubly excited states       - detailed energy levels

This energy level diagram shows the binding energies of the ground state,
ortho-helium, parahelium singly excited states, the ionization threshold state and
the spectrum singly ionized helium - and the threshold for doubly ionized He - the alpha-particle

The electron repulsion "pushes" the doubly excited states of He to regions above the
    single ionization threshold   ( see diagrams on autoionization below )
so that all doubly excited states are autoionizing states
                (    this is not allways the case for other Z than 2, but very energy relations shown below are valid )

A de-excitation via an autoionization is often calle Auger process or non-radiative transition as opposed to radiative deexcitation

xcf_0110_Doubly_excited_States.png

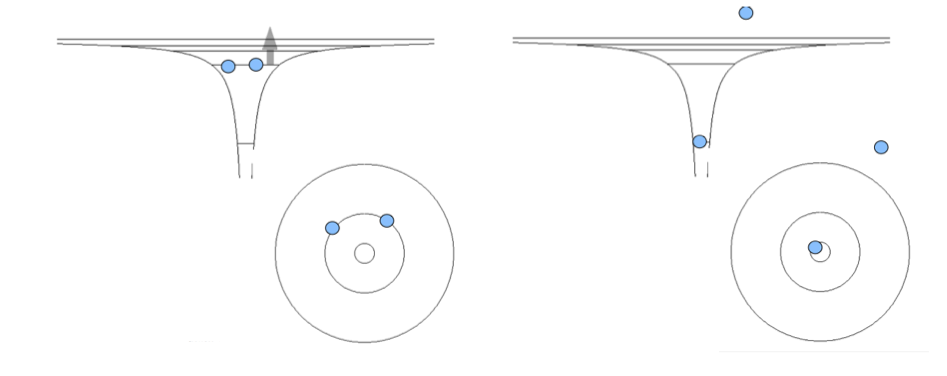
Doubly excited states energy diagrams

xcf_0115_Doubly_excited_and_de-exciting.png

Doubly excited states - AUTOIONIZATION

The energy is conserved;
We see that the sum of energies in the second and third picture
are EQUAL. Therefore the system can go from one to the other state - no energy involved

The first picture - to get there, we must somehow excite 2 electrons at the same time

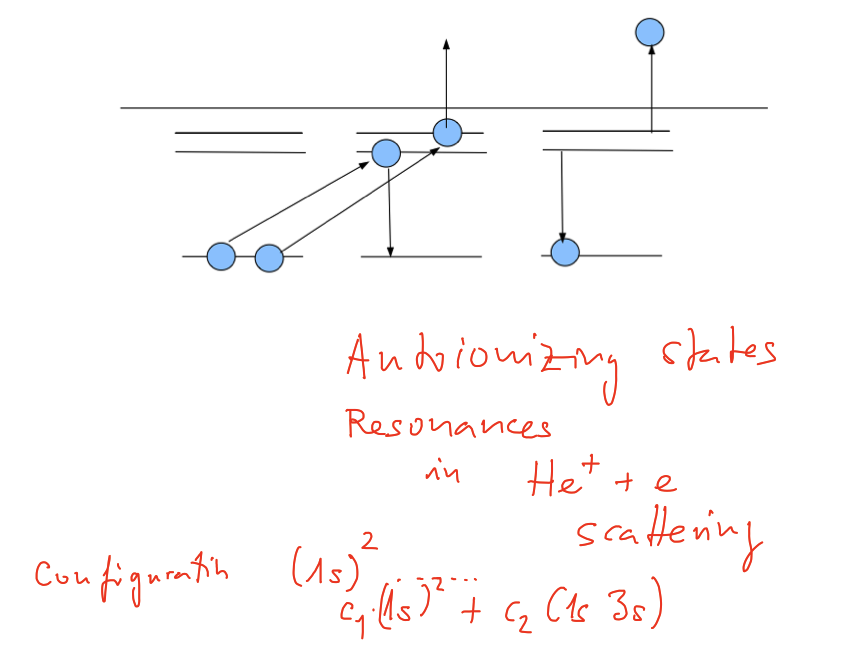
xcf_0130_Autoionizing_states.png

Configuration mixing - formal argument - Expansion in a basis

xcf_0200_Configuration_mixing_from_expansions.png

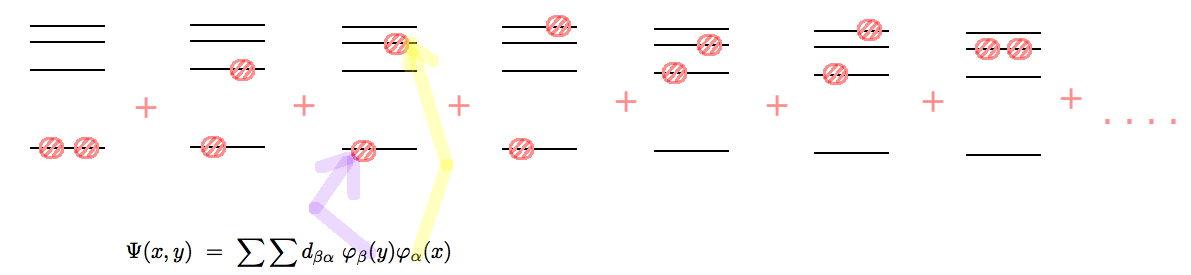
The above formal configuration mixing formula illustrated as a sum of energy-level diagrams

configuration_mixing.png

The concept of configuration mixing is important in many areas of quantum many-body theories;
For atoms, molecules, solids, Nuclei etc ....