Links are given below.
Matlab scripts are available - some are linked to, some will be made available later (they need editing)
The radial functions and spherical harmonics are in hydro_YLM/index.html and
the last part of this page is also in visual_N_5_L_2/index.html (for a simpler look)
Most of the basic topics which we might need are covered for example in these LINKS:
Hydrogen atom wavefunctions http://en.wikipedia.org/wiki/Hydrogen_atom#Wavefunction
Laplace operator http://en.wikipedia.org/wiki/Laplace_operator#Three_dimensions
Legendre Polynomials http://en.wikipedia.org/wiki/Legendre_polynomials
Spherical harmonics http://en.wikipedia.org/wiki/Spherical_harmonics
Table of them http://en.wikipedia.org/wiki/Table_of_spherical_harmonics
List of Radial functions: http://en.citizendium.org/wiki/hydrogen-like_atom#List_of_radial_functions
see also the whole article http://en.citizendium.org/wiki/hydrogen-like_atom - better than wikipedia
National Institute of Standards and Technology (NIST) atomic data databases http://www.nist.gov/
See also https://en.wikipedia.org/wiki/National_Institute_of_Standards_and_Technology
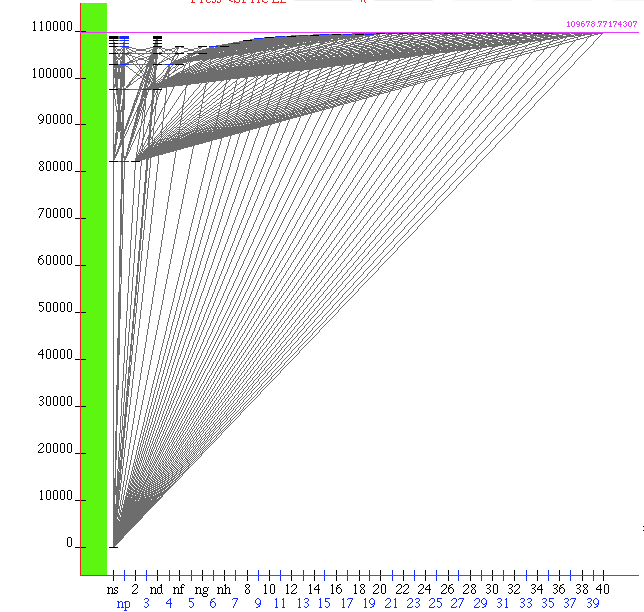
Spectrum of hydrogen from states up to L=40 - details remain hidden due to resolution
This is a Java Applet at http://physics.nist.gov/PhysRefData/ASD/lines_form.html - The Grotrian Diagram (Java)
/ unfortunately, Java Applets might soon be forbidden in all browsers - keep one old for your studies ... /
see also last year's 2014_08_26/index.html
zNIST_hydrogen_2015.png
Spherical coordinates; Laplace operator in spherical coordinates
Kinetic energy - separates to radial motion and the angular momentum squared term - just as in classical physics
for RADIAL POTENTIALS - or as we say spherically symmetric potentials - potential depends only on distance r
Operator denoted Lambda squared
xcf_1000.png
A partial-differential equation is "separated" to several (two) equations in subsets of variables
-- if the differential operator (must be LINEAR) can be written as sum of terms depending each on one of the subsets
Here we show this for a case of totally TWO variables, the total diff. op. L can be written as a sum of L_ksi and L_eta
Then some solutions can be found as PRODUCT of two functions.
Assuming one such solution, we find that the equation separates into two equations - because of each term is seen to be a constant
A general solution can then be a sum of various such product solutions - due to the LINEARITY of the original differential (partial) operator.
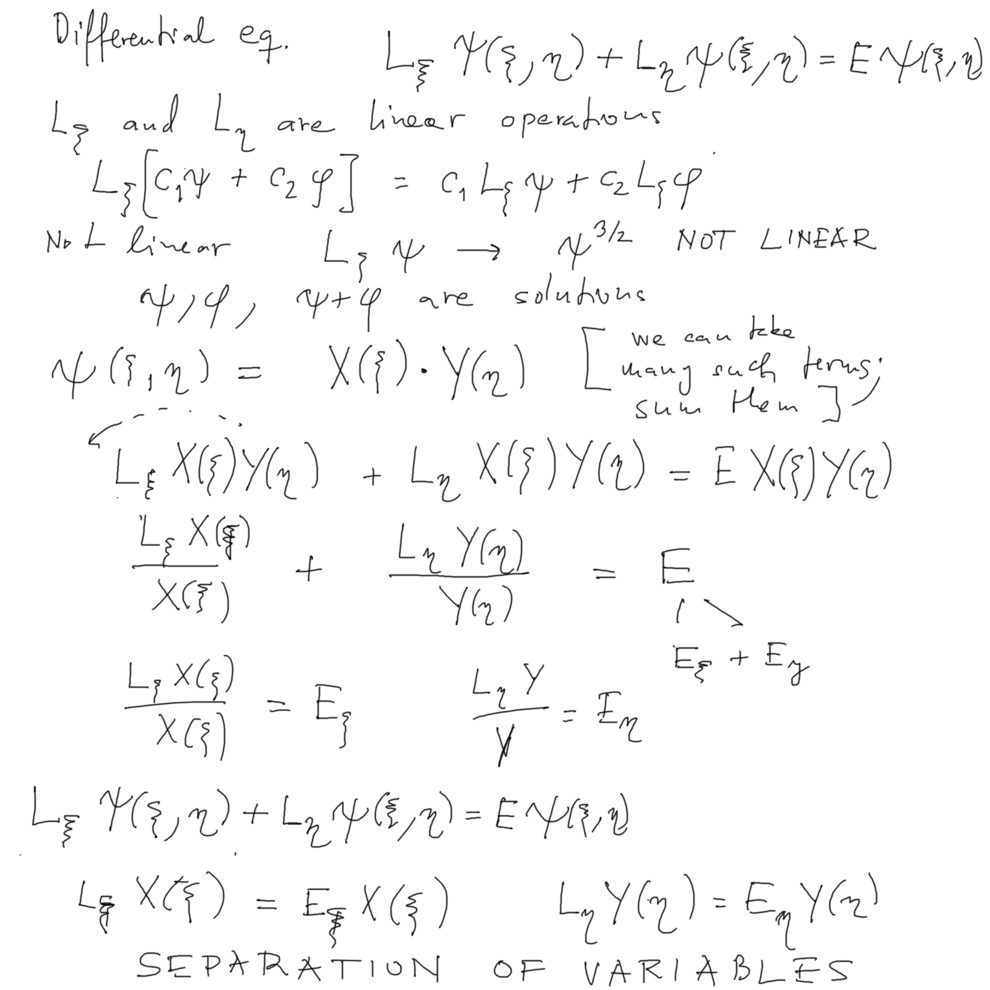
xcf_1010.png
And the equation for so called SPHERICAL Harmonics
The type of spherical harmonics used in atomic physics might differ from spherical harmonics used in other fields
(e.g. chemistry - there are often used the "real spherical harmonics" - linear combinations of those used here )
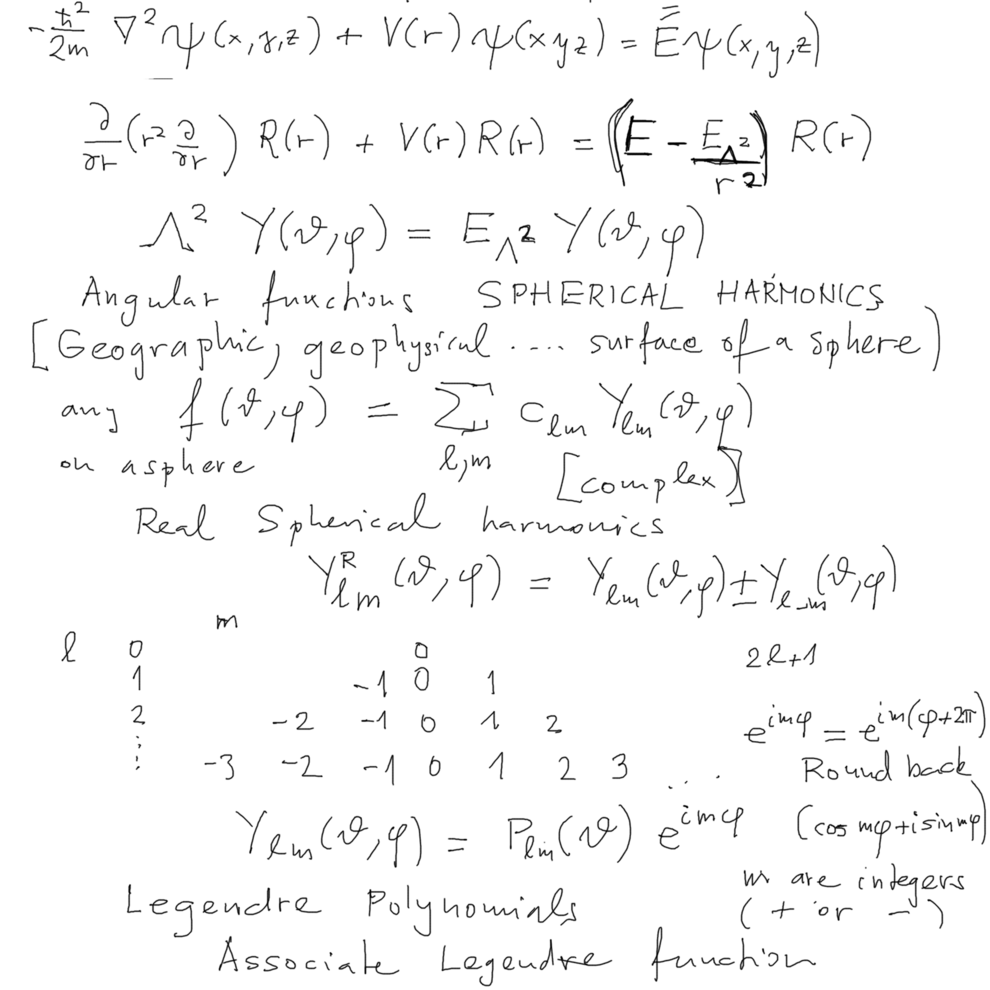
xcf_1020.png
... Orthogonal polynomials; orthogonality of functions; expansion in sets of functions ..... etc
xcf_1030.png
hydro_YLM/index.html this contains both the the polar plots of Spherical Harmonics and the plotting of Radial Functions and densities.
Polar plot - theta from 0 (up) to pi (down) - phi goes the 360 degrees - 2 pi. Just like the geographic system, but there theta goes from -90 to 90.
(and the mathematics would be slightly uglier for our integrations)
xcf_1040.png
List of Radial functions: http://en.citizendium.org/wiki/hydrogen-like_atom#List_of_radial_functions
( see also the whole article http://en.citizendium.org/wiki/hydrogen-like_atom - better than that on wikipedia)
z-Psi_hydrogen_citizendum.png
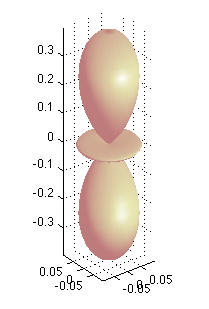
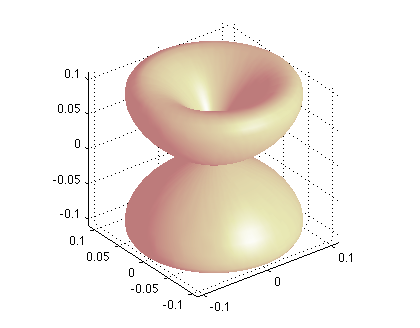
There are many examples - usually one shows the spherical harmonics, and the radial functions
We have seen at those, but below are also visualizations of total "probability density"
A systematic comparison is given at the end
See the details in hydro_YLM/index.html
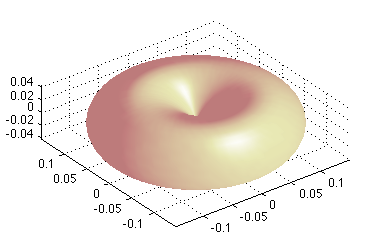
z_0012_Matlab-Doughnut_M-equal_L-rotation.png
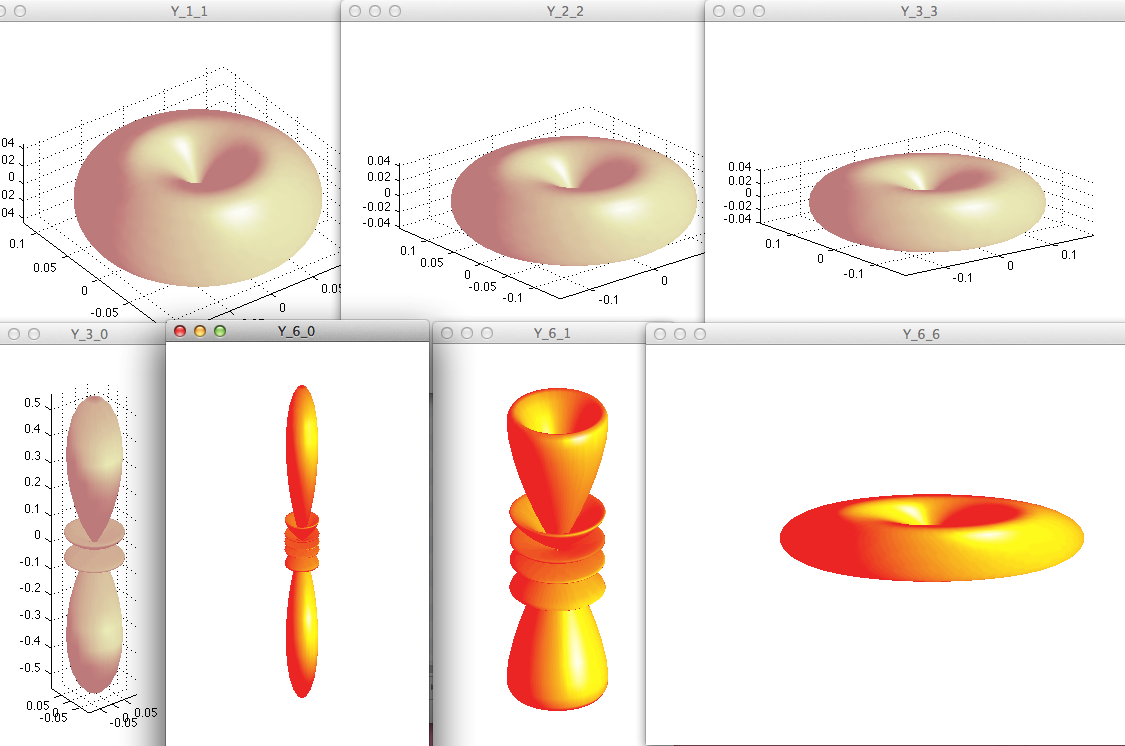
z_0012_Matlab-Doughnut_M-equal_L-rotation.png
zPsi_7_3_2.png
zPsi_7_5_3_newcol.png
zPsi_5_3_2.png
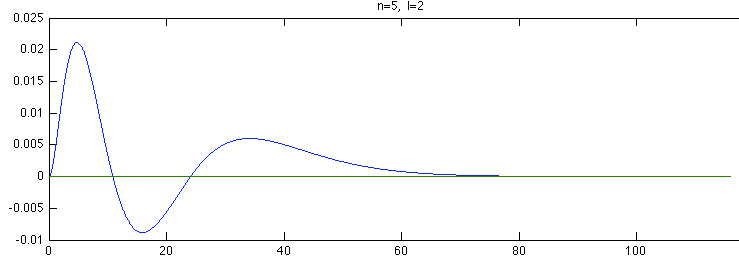
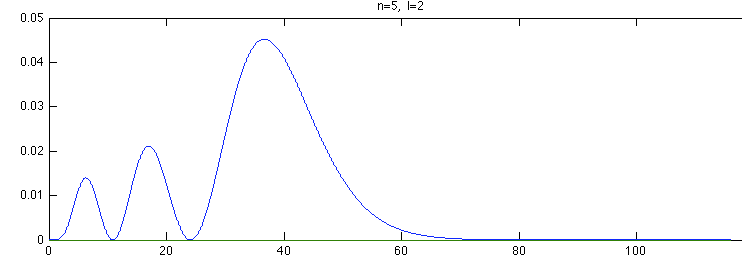
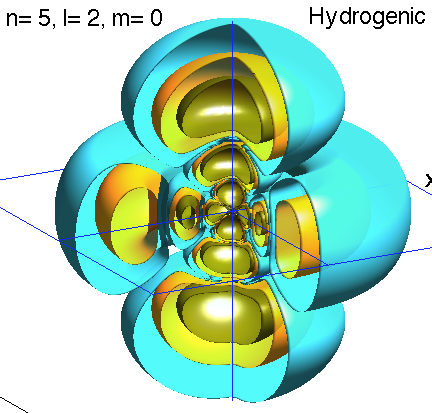
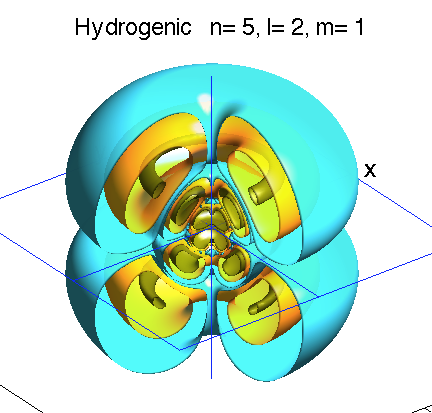
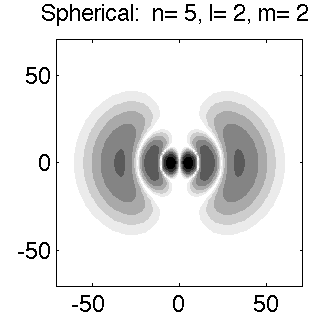
Below is a systematic comparison of all the features for n=5 l=2 m=0, 1, 2
Computer Algebra in Matlab - the radial function ( so
called pretty-print in 1980-style )
