Light and atoms - Part 1
Quantum mechanics of time developement
Stationary states - eigenstates of H vs superpositions of states
An eigenstate of H - eigenvalue of Energy - stationary probability distribution - NO CHANGE

sc_0100.png
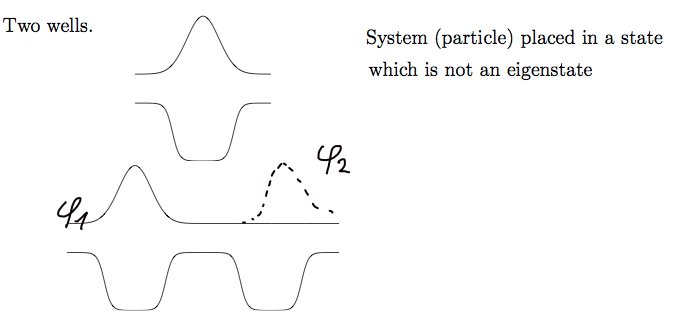
We discuss first a very simple problem - two identical potential wells for one electron
The state in one well is known - what happens when 2 wells are present
First generally about superposition of 2 eigenstates - the original simple sum will be
modified by the additional phase
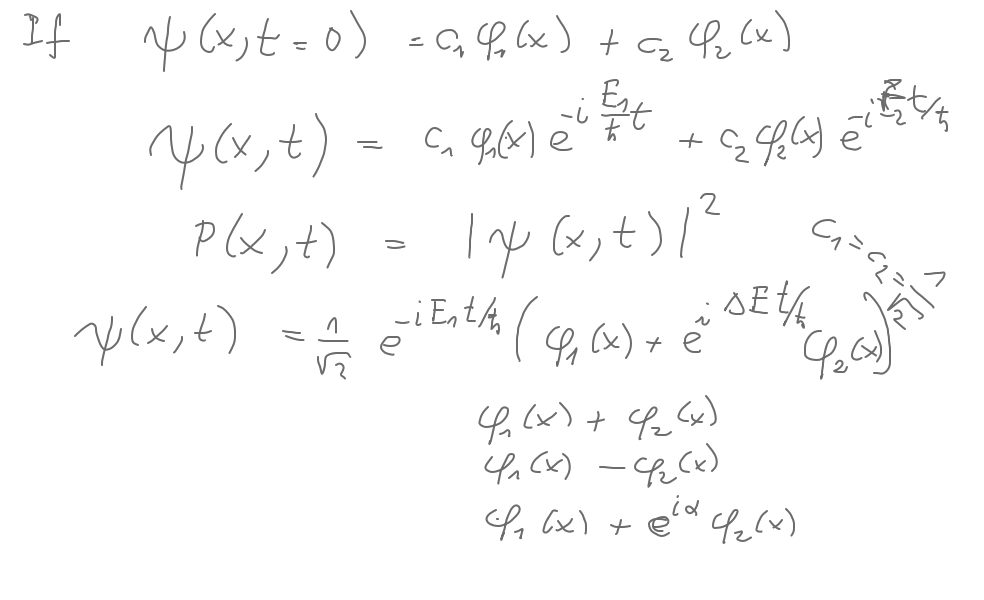
In the above: TASK consider phi1 to be an 1s-state and phi2 an 2p0-state - opposite parity. Their superposition will be
a density concentration on the positive z-half. As the phase changes with time, it can become also simply (-1).
What would happen? Make a sketch of the situation - for simplicity you can draw a similar 1-dimensional problem.
The 2-well animation spread out in time
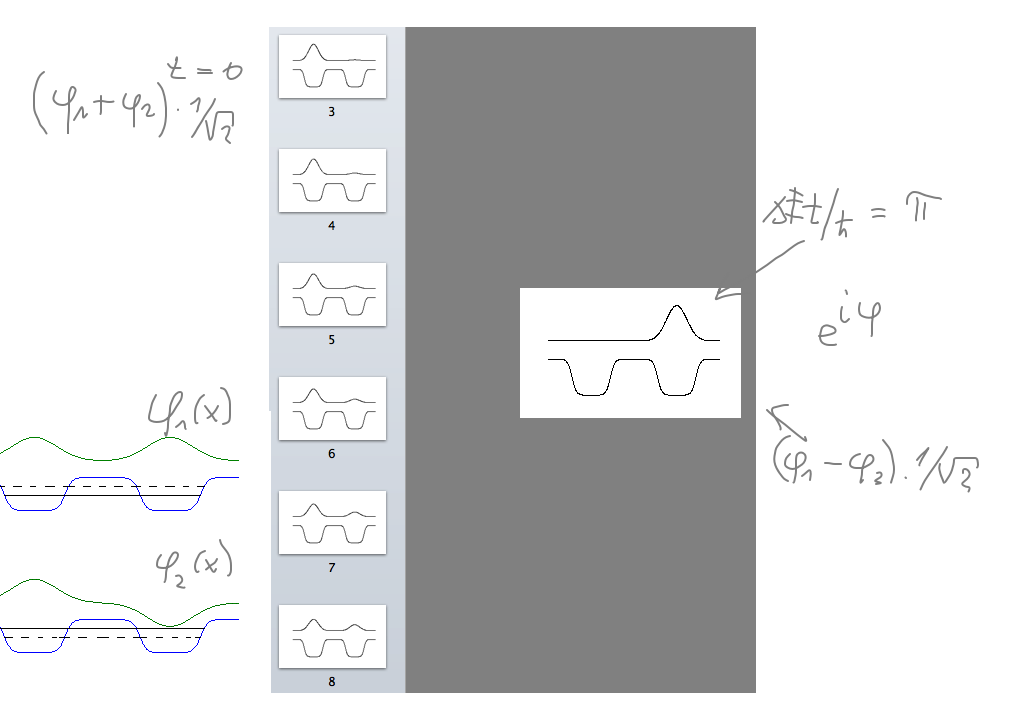
sc_0300.png
Well known result illustrated by animation (copied from last year)
 |
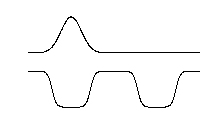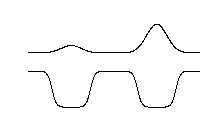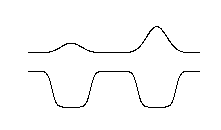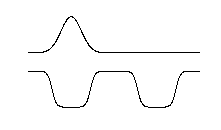 This animation shows time developement of PROBABILITY DENSITY |
We know that eigenstates of the whole H = H0 + V1 + V2 form a sort of split doublet (if the wells are moderately separated)
More details are below
Physics: the "electron" is placed in a state at t=0 confined to ONE WELL ONLY (1 well eigenstate)
The probability is seen to be OSCILLATING between the two wells
This is seen from the EIGENSTATES of the whole problem
Note that we discuss two "sets" of state, the phi - eigenstates of simplified system, and the psi eigenstates of the whole
system
The probability flows back and forth in this simple case.
There are many realization of this 2-state time developement, usually described by the following matrix
| a b |
| b* c |
Here we model it by two wells ( b is then a probability amplitude of transfer from one well to the other )

sc_0400.png
We assume here that the approximation of states being linear combinations is sufficiently precise
( we should remember that the actual solutions must be somewhat different; if the wells
are "further from each other", this approximation is better. However, this is a detail not important
for the understanding of the mechanism )
Note that there are two set of states as indicated - this will be discussed several times below

sc_0500.png
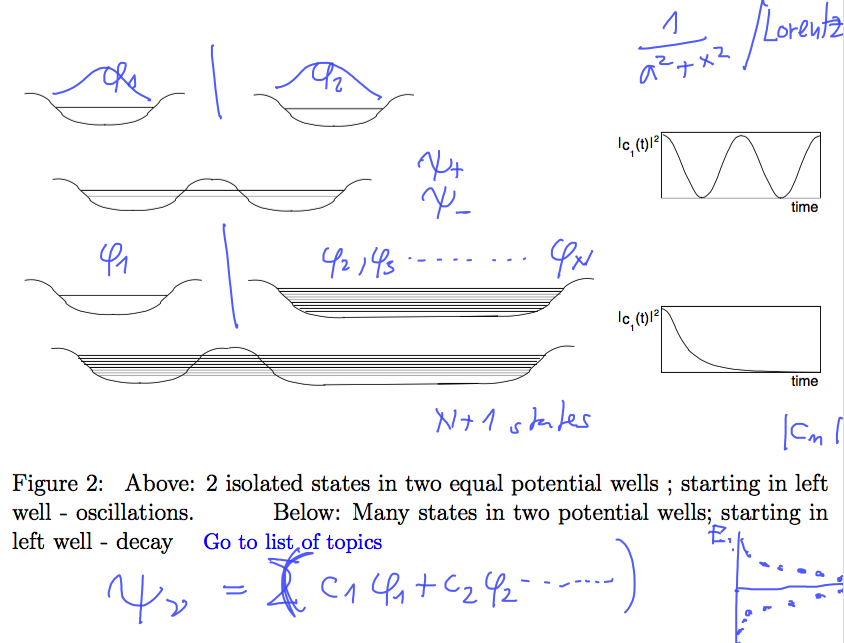
In 2-state ( 2 well ) case we get the 2 eigenstates (which are stationary - but delocalized - probability to be "both places" )
One possible description is in terms of the two eigenstates
Now considering the "asymetric case" - where the other well has a "quasi-continuum" of eigenstates
There will also be "splitting", there will be N+1 eigenstates
The "amplitude" of the "left" state in each of the eigenstates will be roughly such that
its square follows
the Lorentz profile - this will be also discussed later see next lecture here
In this asymmetric case, the probability simply "flows away" - if N is large enough
- exponential decay in the continuum limit
sc_0600.png
Solving TDSE - Time Dependent Schrödinger Equation - by expansion in eigenstates ODE ordinary diff. equation
This can be done exactly ( as exactly as the expansion is) - by solving the below shown system of couple ODE
or
it is used as a basis for so called Time dependent perturbation theory
Below - Solving TDSE using expansion with time-dependent expansion coefficients

sc_0700.png

sc_0800.png
Solving TDSE using expansion with time-dependent expansion coefficients
Time dependent perturbation theory
in simple terms it is an assumption that the initial state basicaly continues to be close to 100%
while the amplitudes of the "final states" remain very very small forever
Here, eventually, it will be used for finding not the probabilities, but rate of change of the probability
In some other applications, the actual probability is estimated (atomic and molecular collision theory etc)

sc_0900.png
NEXT: Fermi Golden rule
The natural line width
Density of states for photons