Light and Atoms Part 4
1. Overview of the time-development - and harmonic systems
2. Electromagnetic waves - the field - and quantization
3. The model for an atom and the field
4. Putting it all together - Golden rule evaluation
5. Approximations
6. Discussion of the result - Atomic units
First plate:
Golden Rule - recall the 1 level embedded in continuum of the other type levels
Our system - 2 subsystems
the atom
the field (... its collection of eigenmodes)
actually, each eigenmode has its own Harm.Osc.-number state
The interaction part Hint - still not described ( denoted also as HI )

00010.png
Some of the features of radiation mode electromagnetic field - no scalar potential; E and B symmetric, Vector "potential" A
Gauge invariance with respect to modifying vector and scalar potential

00023.png
Wave equation for A; we can quantize A - i.e. eigenmodes of the A-waves; The energy of the field (energy density)

00024.png
To set up the quantized field - we need the transformation to the dimensionless analogues of Q and P in the Harm.Osc. part
Shortcut - since we do not have the "displacement" idea in a simple way - but we have
two expressions for total energy - the integral over density - and the sum over number operators
The requirement that these two are EQUAL leads to the complicated pre-factor in the square root (eq. 43 in the snapshot)

00025.png
Towards the discovery of the Hint ( denoted also as HI ) - the hamiltonian via lagrangian
A short reminder of what is the Lagrange method; Newton equations, potential energy; this only for conservative forces

00040.png
This is to remind us about no scalar potential; but the Lorentz Force is general (this plate reappears modified below)

00045.png
( Here we started by remembering the "current" .... )
The interaction term is derived from the hamiltonian of a charged particle in electromagnetic field
which appears as a modification of the kinetic energy term
Note tht the relation p = m v is not valid any more - we should return to this point later

A4.png
Summary of the model - and the interaction term

A5.png
Applying the Golden Rule

B1.png
Why is there the "electron" coordinate in the description of the FIELD
The field is described in terms of the eigemodes - but each eigenmode is present in the the space points
( see the eigenmodes "displacements" in the vibrating chain example)
Finally, all the dimensional quantities are collected

B2.png
The final expression for the rate - discussion of the angular integration ( here taken in a very short version
we should return to this point)

C2.png
Schematics of the matrix element evaluation ( the field quantities are blue, electron quantities are red )
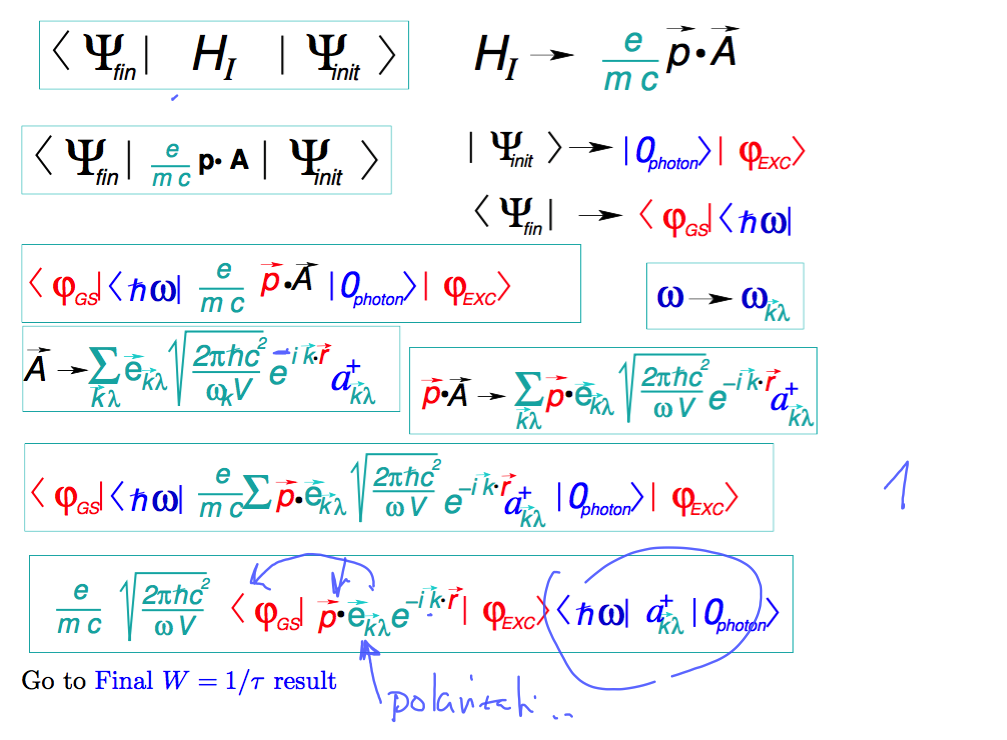
C4.png
So called dipole approximation - this leads to a simpler expression
also called long wavelength approximation

A6.png
Discussion of the final expression for the transition rate and the associated "lifetime"
transformed to atomic units - the fine structure constant alpha to the third power!!
- it scales with Z - fourth power

C6.png
Next time: Summary;
missing steps and clarifications;
STIMULATED EMISSION