1. How to work with continuous systems - fields - in Quantum Mechanics - Vibrating systems
2. Normal modes of harmonic systems
Normal modes of coupled vibrations
3. Normal modes - total energy is a sum of energies in normal modes - independent oscillators
4. Quantum mechanics of a Harmonic Oscillator - Algebraic Method
5. "Quanta" - creation and anihilation operators
Review of the last work: the Quantu mechanics of time developement in one slide

sc_0100_resume_of_time-dependent_QM.png
Continuous systems --> Discretization, Mesh of points
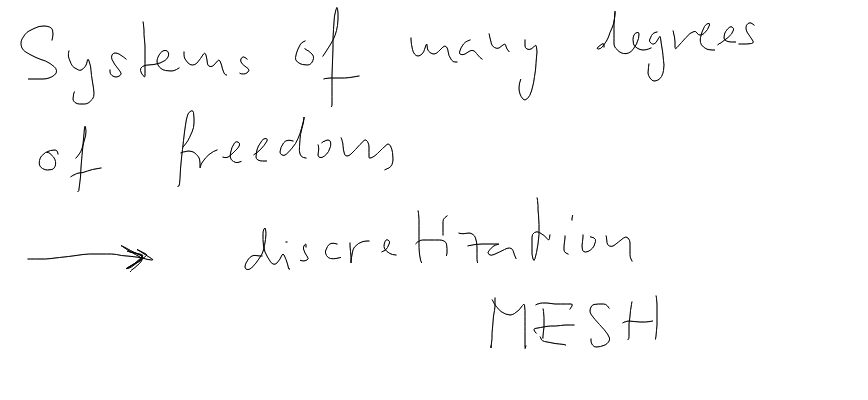
sc_0200.png
Topic in classical mechanics: Small vibrations (i.e. LINEAR SYSTEMS) Normal modes or Eigenmodes
In the following - Linear algebra; From one particle to a system - coordinates placed in a column vector
scalar product matrix product of transverse (row vector) with the column vector in question
"coupling terms" - nondiagonal terms in a matix
(for generality - we allow that also the "mass matrix" can be present - usually that will be diagonal)
Finding the eigenmodes - means than finding the eigenvectors and eigenvalues of the problem - as outlined below

sc_0210_General_coupled_oscillations.png
We ( from Goldstein's classicalt book ) even get all new "masses" equal to one
and the original total energy
is then written as a sum of independent terms (no matrix, no coupling)
These resulting independent oscillations we call normal modes - or eigenmodes

sc_0220_NORMAL_MODES_coupled_oscillations.png
Examples - vibrations of a "string" or "rope" realized as "discretized" into balls on strings
the dynamic variables are then the displacements un of each "ball" - kinetic energy straightforward;
the deformation energy of each string is 1/2 k ( un - un )2 where k s the string constant - see later how it relates to frequency omega
( this comes in the section on a single Harmonic oscillater later)
In 1 dimension - only longitudinal displacements - but we plot them in the y-direction
Also - relation between the shown sum over eigenmodes and Fourier expansion
For large systems the normal modes will be of sine / cosine form
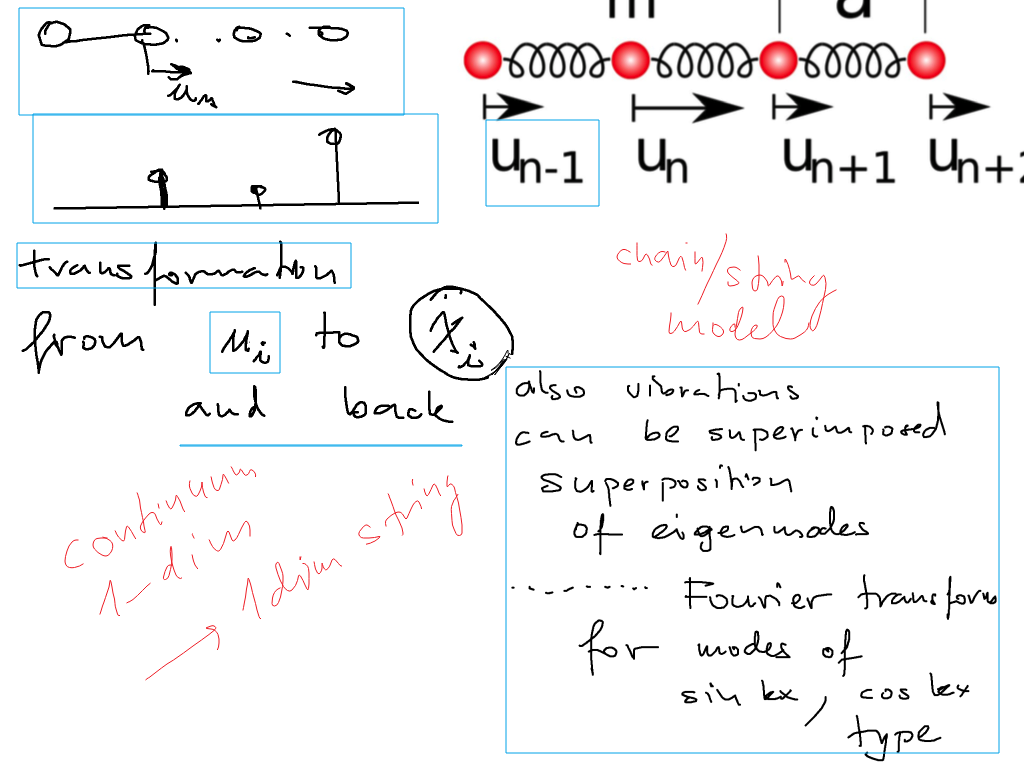
sc_0300_rope_as_string_of_balls.png
The eigenvalues (eigenfrequencies) and eigenvectors (eigenmodes) can be visualized by a simple matlab code
The coefficients of expansion are shown as y at the position of n*a
The diagonalized matrix is shown below for the case N=10
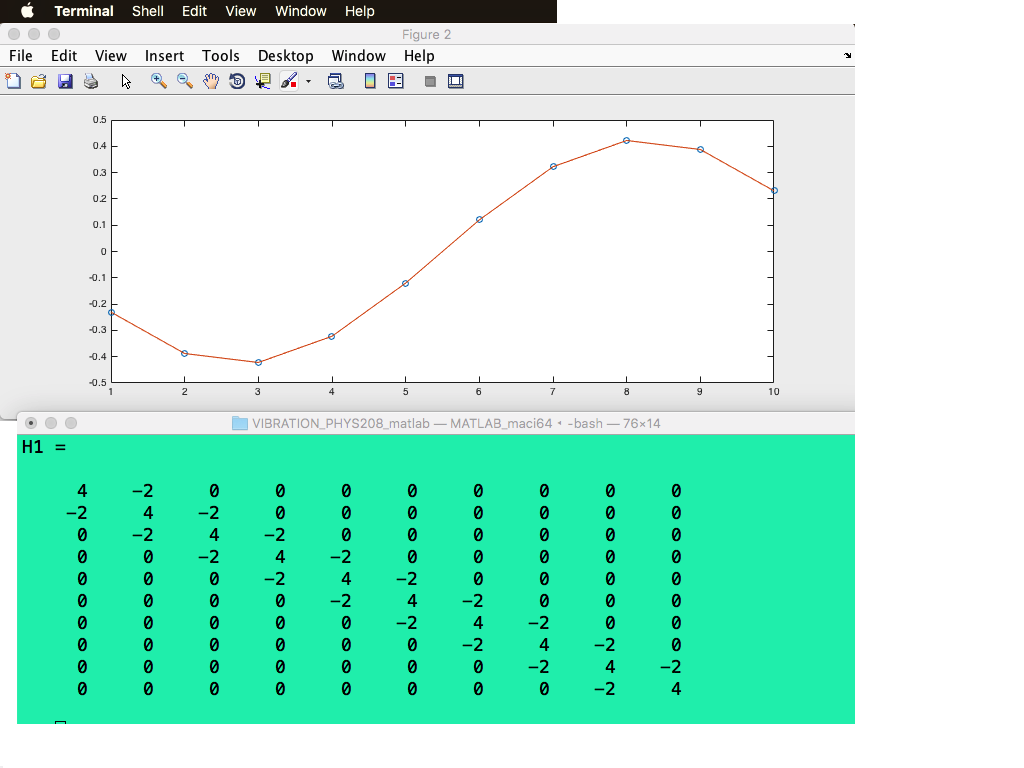
sc_0400Matlab_eigenvalues_matrix.png
More about the vibrating (longitudinally) strings
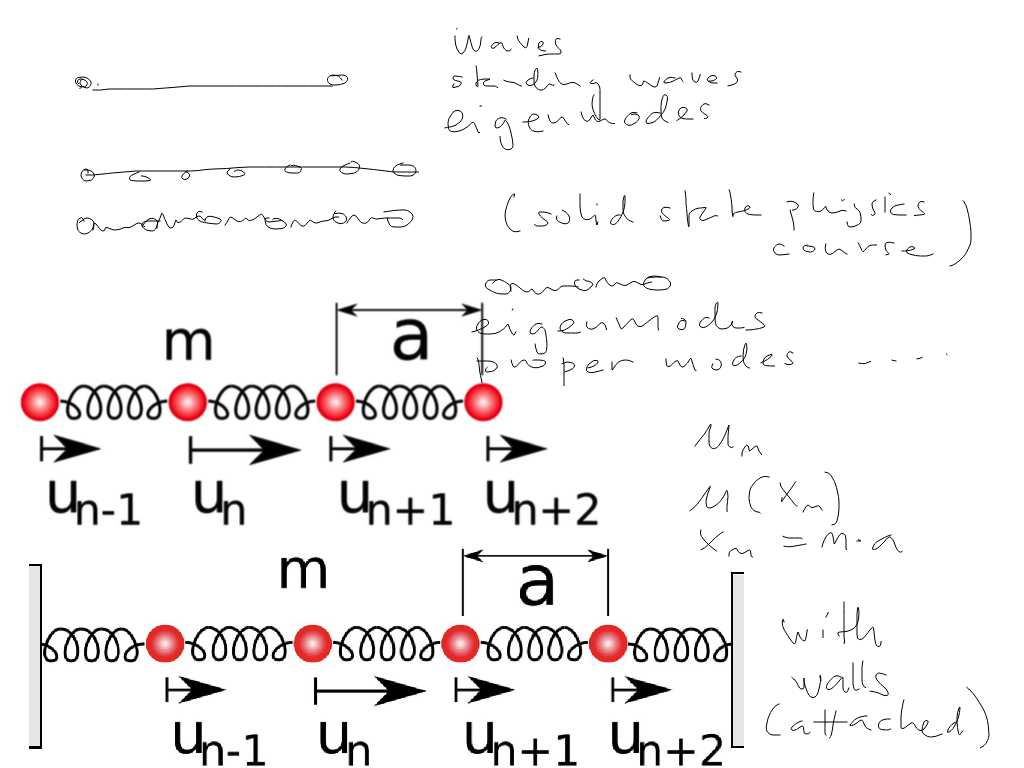
sc_0500_waves_in_1-dimension.png
ANOTHER MODE from the above matlab code ...
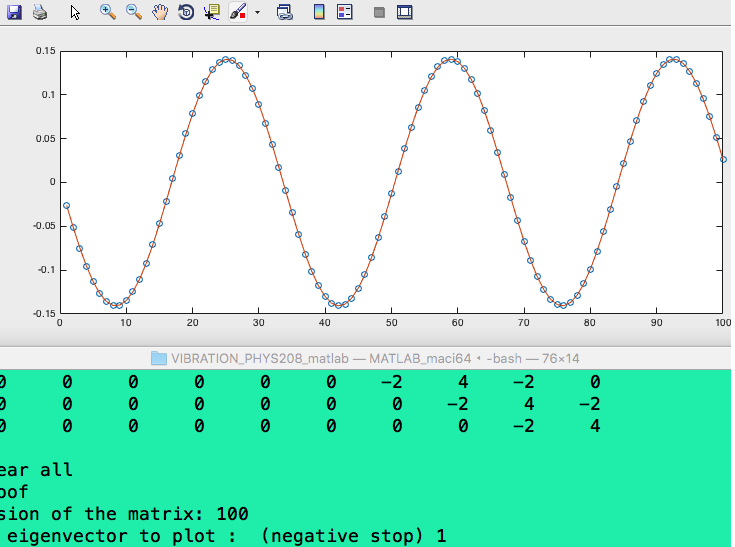
sc_0700_Matlab.png
Algebraic method for an harmonic oscillator
the variable is not x but q - and the tricks are to transform q and p to dimensionless Q and P - with hbar omega as the
energy scale factor Remember omega is 2 pi times frequency f
( and note that we rewrite the "spring constant" k in terms of omega and mass )
So the commutator for dimensionless Q and P is also dimensionless
see operators a and a+ - just clever linear combinations of Q and P
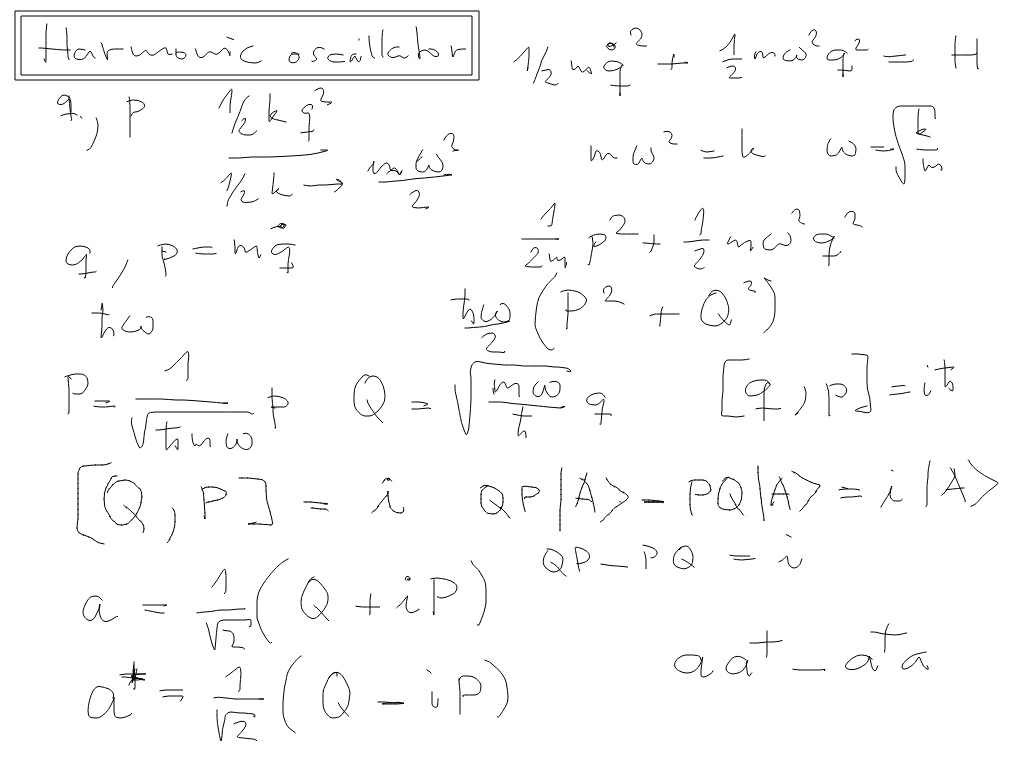
sc_0800_Algebraic_Harmonic_Oscillator.png
Commutator of a and a+
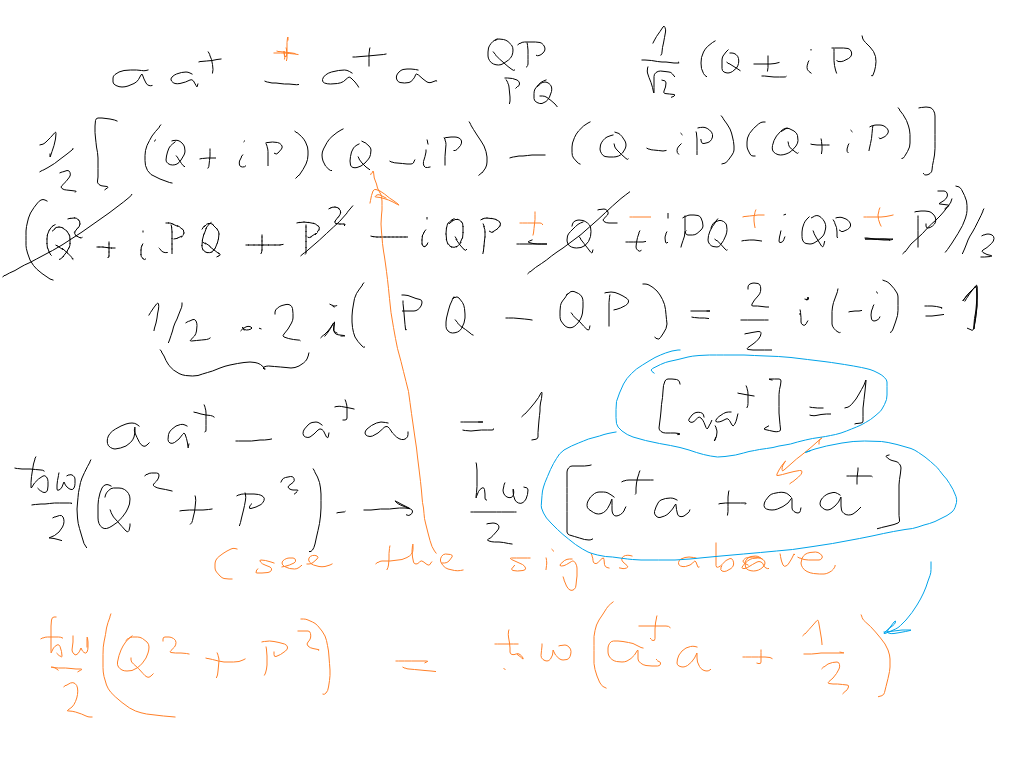
sc_0900_Harmonic_Oscillator_transf.png
Towards the Number operator N = a+ a and further commutators
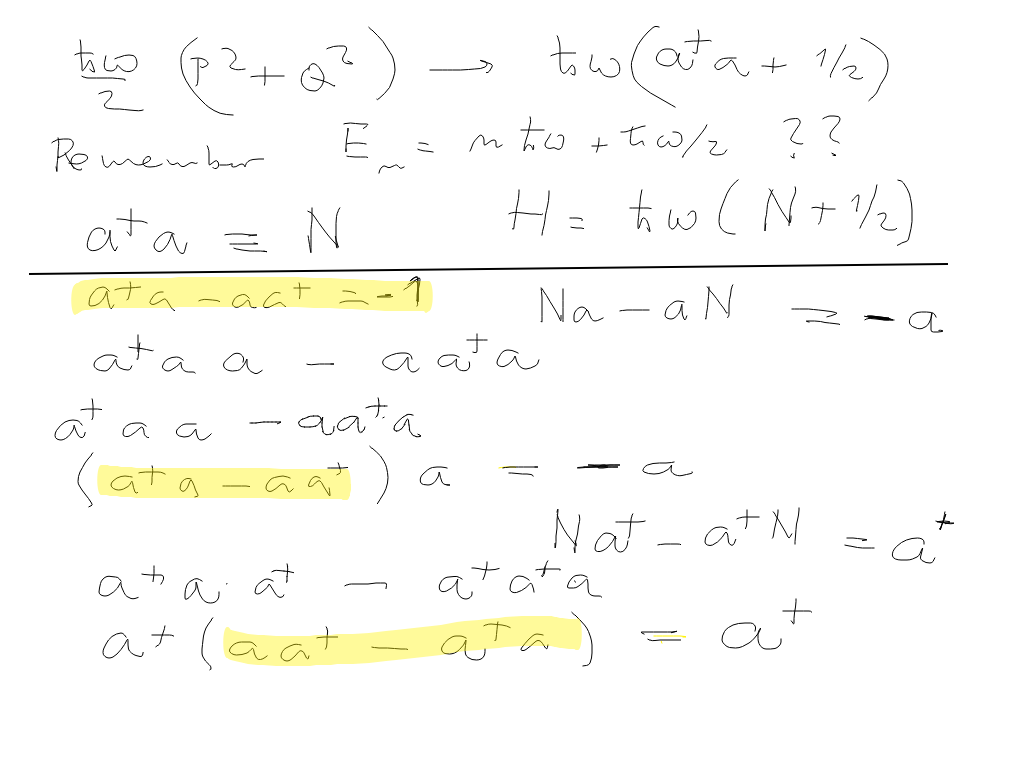
sc_1000_Harmonic_Oscillator.png
Commutator of N = a+ a a+ and a

sc_1100_H.O._Number_Operator.png
| And the states of Harmonic oscillator are described as eigenstates of N and connected by the ladder operators |

sc_1200_H.O._Number_Operator.png
And the states of Harmonic oscillator are described as eigenstates of N and connected by the ladder operators .....
a+ is a creation (of an energy quantum) and a is a anihilation (of an energy quantum) OPERATOR
operating on the (simultaneous) eigenstates of N = a+ a and H (because H is N times const1 + const2)
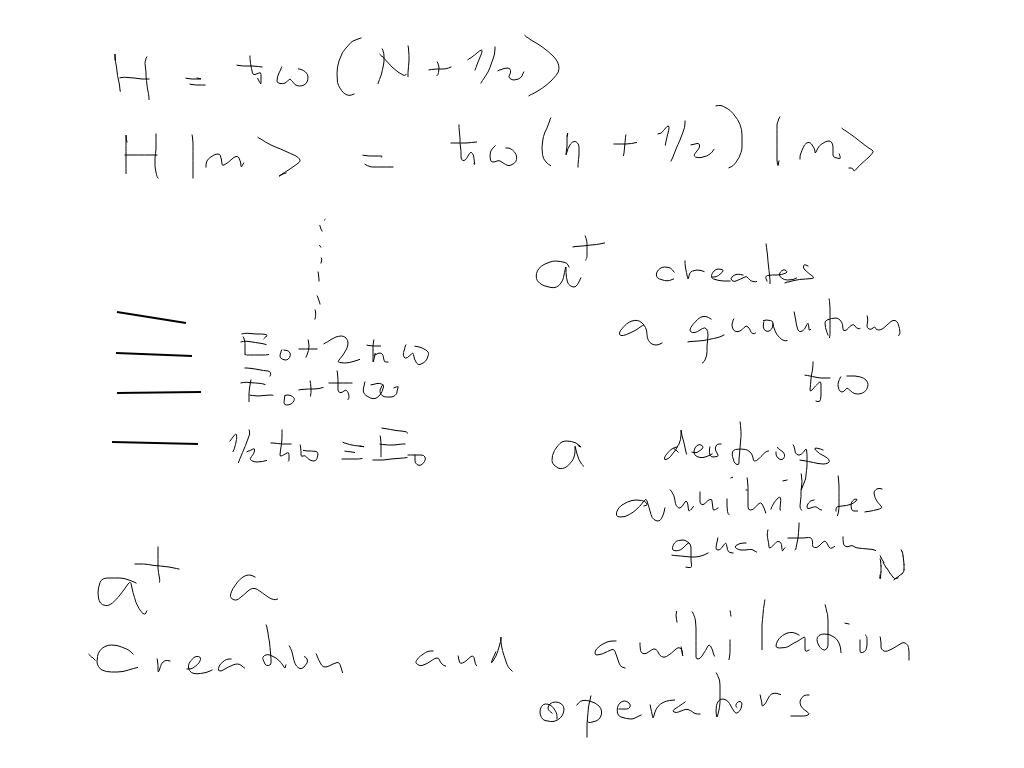
sc_1300_creation-annihilation.png
Summary and spectrum

sc_1400_creation-annihilation.png
The above story in the notes (mostly) Highlighted the commutators

sc_1500_Number_operator_print.png
The above story in the notes (mostly) - with numbers instead of a

sc_1600_creation_anihilaton_print.png
There is also one more aspect of the method: we get the expression for the ground state
with the help of a first order equation only
And all the other states by repeated application of derivative and multiplication
A simple way to generate the Hermite polynomials!

sc_1700_next_time.png
Next time: 1. closing this Harmonic oscillator part;
2. How to apply all of this to the Light - atom interaction (particle in El-Mag field etc)