PHYS261- Atomic Physics and Physical Optics
Atomic physics Part PHYS261 - main topic list
- see also detailed Overview of the
course - both parts
- 0 - Physics of atoms - Introduction - Hydrogen-like
- 1 - Helium and two electron atoms
- 2 - Many electron atoms
- 3 - Light - Atom Interaction
INTRODUCTION - Quantum Mechanics and Hydrogen Atom
See also last year - ../2012_09_04/
Hydrogen atom - in all courses of Quantum Physics. This year - 100th
anniversary
of Bohr's atom model - July 1913 - Old Quantum
theory; Quantum mechanics 1926 to 1927
Proton and electron, interacting Coulomb interaction (not a
"spring"... )
Coulomb Force - potential energy GAUSSIAN SYSTEM OF ( units )
THINKING (Length, Mass, Time; no current )
( i.e. no 4 pi epsilon zero !!! - see later )
Force - if integral over work changes independent of
path - Potential energy depends on position
Newtonian mechanics with "conservative" forces - potential and
kinetic energy
01_Hydrogen_proton_electron_Force_potential.png

01_Hydrogen_proton_electron_Force_potential.png
In the last lines we jumped from CLASSICAL MECHANICS
to QUANTUM MECHANICS
--- defining the OPERATORS - what do they
"operate" on - and how?
Operation on waves - starting with a PLANE WAVE
Note that UNLIKE in optics, Maxwell waves, acoustics etc where waves
are taken as REAL PART of the complex exponential
IN QUANTUM MECHANICS GENERALLY THE WAVE MUST BE COMPLEX (in some
cases some parts become real functions,
but in the full formulation - as outlined below - the COMPLEX values
are essential!!
We thus start - as probably in history Schrödinger did - by looking
at free particle, no potential - and
start playing with a plane wave.
How can we "operate" - to get the momentum p - this already proposed
by Louis de Broglie in 1923 (3 years before Schrödinger)
02_operator_wave_plane_wave_kinetic_energy.png

02_operator_wave_plane_wave_kinetic_energy.png
In the above picture we have worked out the OPERATOR of kinetic
energy and we are ready to discuss
time dependent Schrödinger equation in the next picture below.
For the hydrogen atom - and for all bound state cases - we solve
the TIME-INDEPENDENT Schrödinger equation
Here is a illustration from our little program - we shall come lator
to the separation of time
When solving for the bound motion - the solution, which provides
PROBABILITY DENSITY - must be
finite everywhere - or at least be integrable over the whole
space - the integrated probability density
- i.e. the probability of being anywhere - must be ONE - 1.
http://web.ift.uib.no/AMOS/schroed/
(
or
older version http://web.ift.uib.no/AMOS/schroed/schroed_0.92.html
)
03b_finding_solution_bound_Schroedingers_Toy_WWW.png
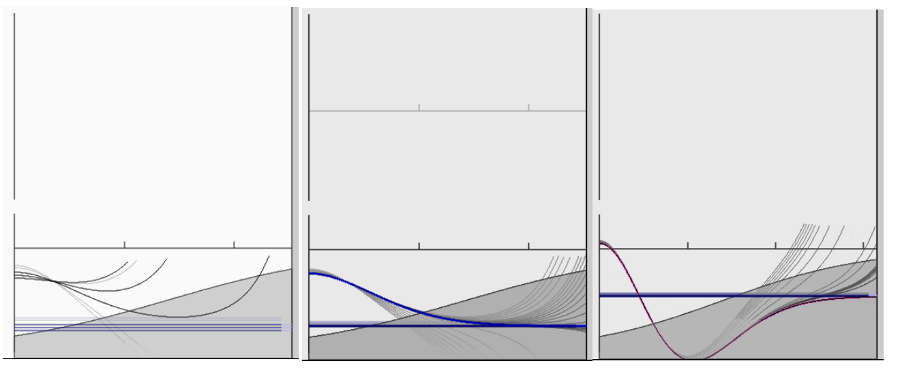
03b_finding_solution_bound_Schroedingers_Toy_WWW.png
As we see - for most energy values the solutions blow up - run to
infinity. Only for some energies
the solutions go to zero for asymptotic distances (positions) - and
thus only those energies
are the physical solutions.
Bound states can only have those discrete values of energy - energy
levels.
Here below we sketched the Schrödinger equation and the bound states
story
TIME-independent form discussed below
03_potential_well_bound_motion_free_motion_quantum_classical.png

03_potential_well_bound_motion_free_motion_quantum_classical.png
TIME-independent Schrödinger equation and the bound states
story - and the preview of hydrogen atom results
The separation of time must be discussed - it will be done in the
next lecture.
04_bound_states_discrete_spectrum_E_nl_quant_numbers_ATOMIC_UNITS.png

04_bound_states_discrete_spectrum_E_nl_quant_numbers_ATOMIC_UNITS.png
The separation of time must be discussed - it will be done in the
next lecture.
We shall also discuss the ATOMIC UNITS and the Gaussian system
( Carl Friedrich
Gauss
1777 – 1855 http://en.wikipedia.org/wiki/Carl_Friedrich_Gauss
)
See also ../2012_09_04/index.html




