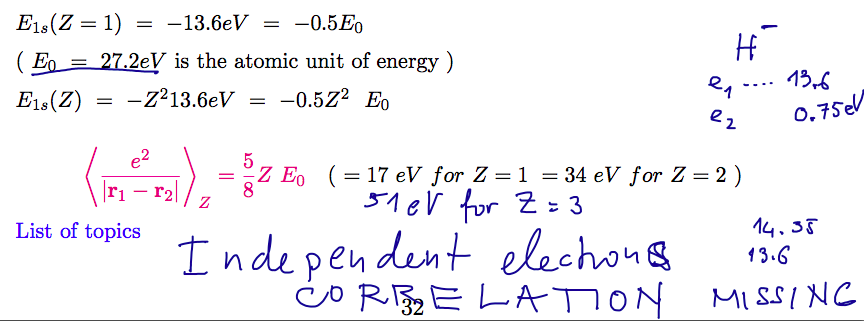Doubly
Excited
States
of Helium. Many Electron atoms - part 1
We also discussed the effective
spin-spin interaction mentioned in the presentation.
This part should be extended -
providing an actual expression from the difference
of the singlet and triplet
energies. (This has not been "captured" )
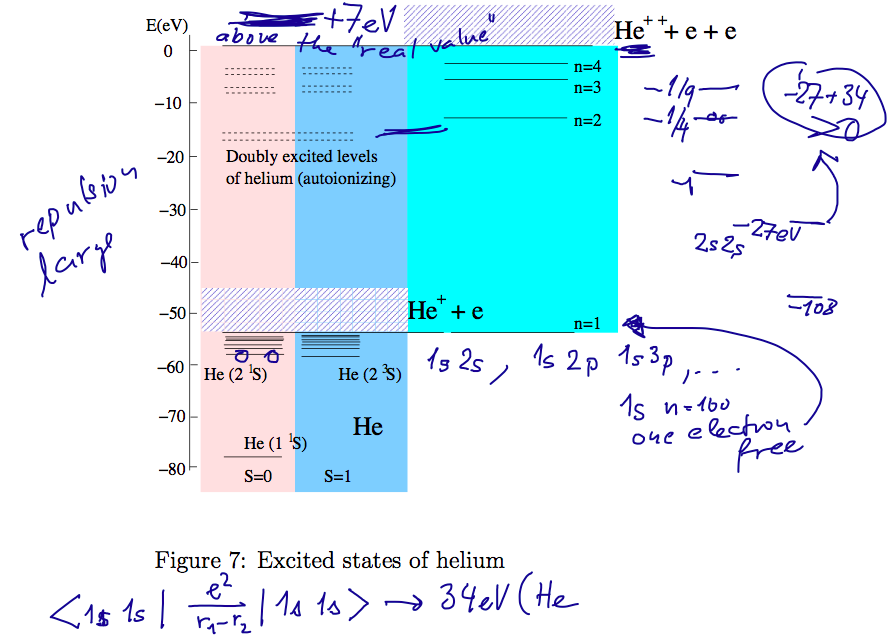
Doubly Excited States of Helium
Doubly excited states will be of the basic
configuration (nl)(n'l') where
both n and l are different from (1s)
Due to the repulsion these states would get quite reduced binding
Here is from the last time - the (1s)2 estimate of repulsion
expectation value (34 eV)
000a_energies.png
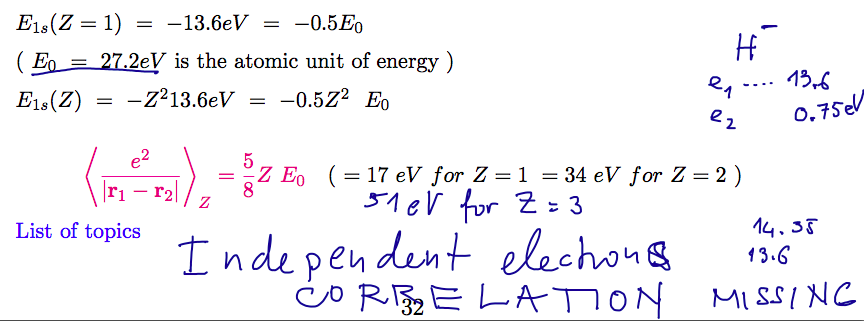
000a_energies.png
If the repulsion matrix element (expectation value) would remain as
large as in the g.s. we have estimated that the
(2s)2 would have a positive energy of nearly 7 eV
But the (2s)2 matrix element is smaller (it can be
evaluated as an exercise, only the same type of terms will appear
as in the evaluation discussed in the previous lecture)
so that the doubly excited levels become degenerate with the
"single-ionized" continuum.
000b_double-excited_states_in_helium.png
000b_double-excited_states_in_helium.png
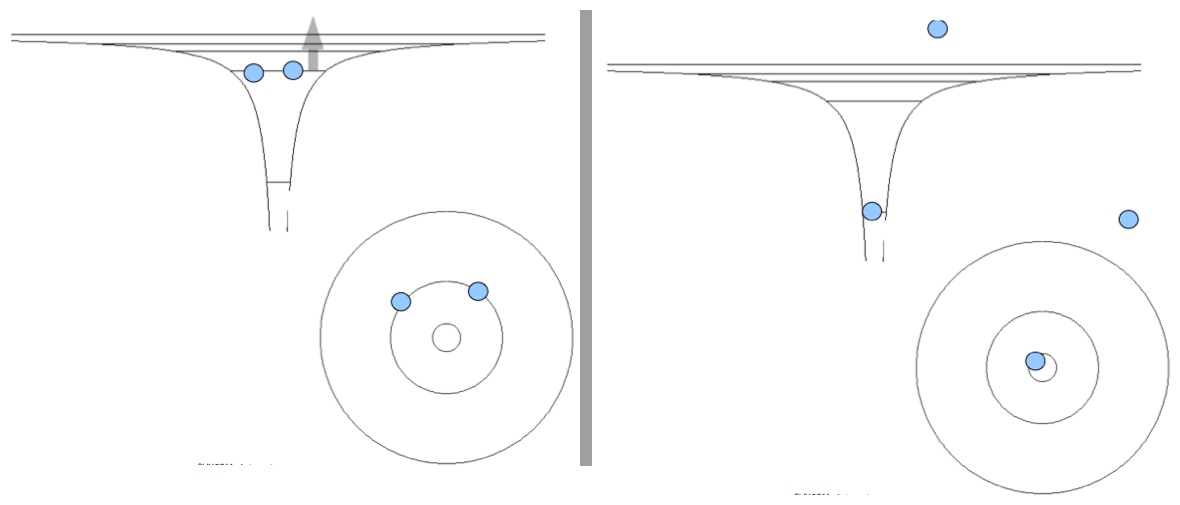
Doubly excited states will thus be "embedded in continuum"
States which have the same energy as an ionized state - as shown on the
diagram
will become AUTOIONIZING STATES
001_double-excited_states_in_helium.png
001_double-excited_states_in_helium.png
The autoionization is in other connections called AUGER PROCESS
Auger process: the initial state is not a neutral atom, but an excited
state of a positive ion,
where the first ionization removed one of the "deaply bound" electrons
(i.e. in many electron atoms)
Many
Electron
atoms
- part 1
The topics discussed in this
first part
002_topics.png

002_topics.png
Pauli principle, antisymmetric functions - Slater determinant
(mathematics of determinants - the same "symmetry")
Oermutation group - also sometimes called Symmetric group of order N -
for N-objects permuted
003_Slater_determinant_1.png

003_Slater_determinant_1.png
See also http://en.wikipedia.org/wiki/Slater_determinant
- after
John
C. Slater who developed many ideas in
description of atoms and
003_Slater_determinant_2.png

003_Slater_determinant_2.png
003_Slater_determinant_3.png

003_Slater_determinant_3.png
Filling of the "ATOMIC SHELLS"
006_filling_states.png
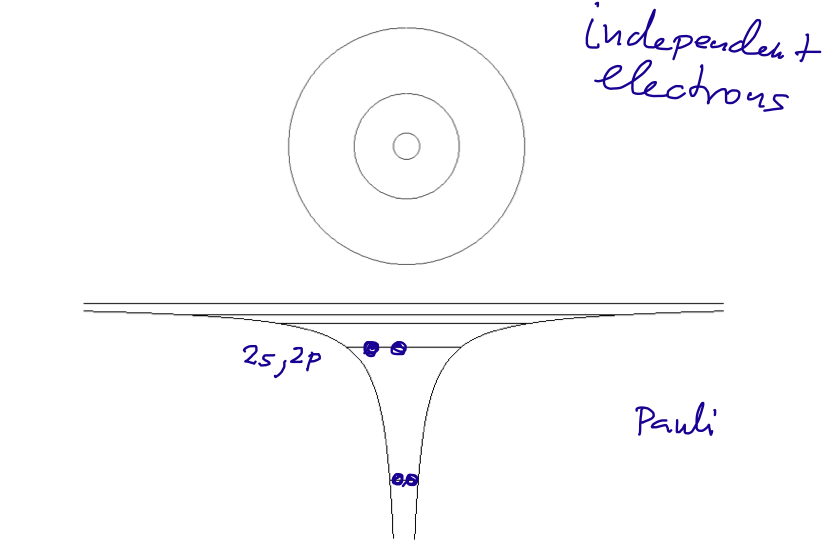
006_filling_states.png
007_filling_states.png
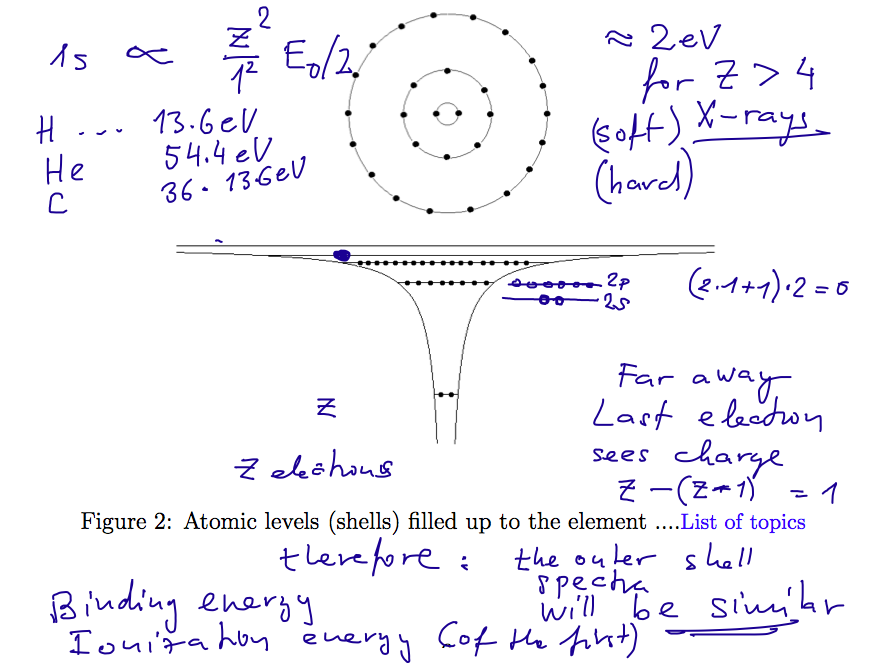
007_filling_states.png
Experimental results for the binding energies of "the last
electron" - or the ionization energies of the first ionization
i.e. the lowest energy needed to lift one electron to continuum in the
neutral atom
008_Ionization_energies.png
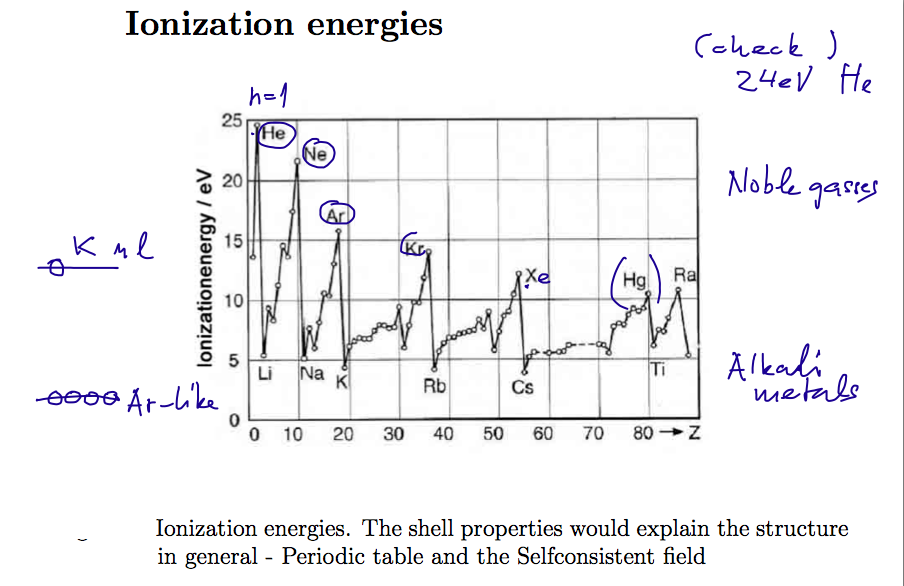
008_Ionization_energies.png
Historically, Hund's rules were very important.
For us they are just an example of the "effecive spin interaction - the
Helium triplet states,
i.e. the Pauli prinsiple - and thus antisymmetry of the space part
009_filling_Hund_s_rules.png

009_filling_Hund_s_rules.png
Towards the
SELF-CONSISTEN FIELD THEORY
interaction of an electron with a "cloud" of charge, the charge
density, and the charge distribution from the probability
- trying to find which potential energy should be used to describe one
independent electron in the atom
(Hartree 1926- 1930s)
010_Coulomb_law_with_a_charge_cloud_and_electrons.png
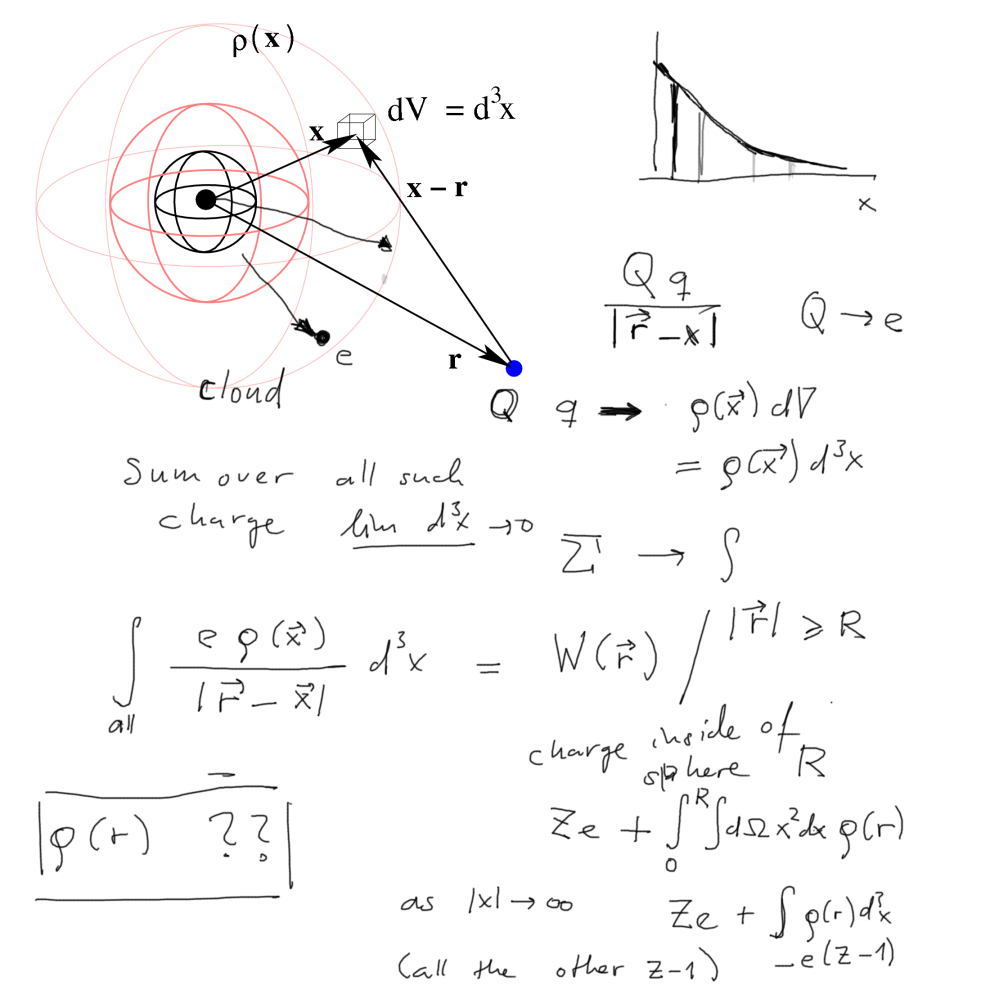
010_Coulomb_law_with_a_charge_cloud_and_electrons.png
The density (rho) coming from the orbitals, but the orbitals are
found
solving Schrödinger equation with the potential resulting from the
density (rho)
020_charge_cloud_Schroedinger_DELF-CONSISTENT.png

020_charge_cloud_Schroedinger_DELF-CONSISTENT.png
SELF-CONSISTENT criterium
022__Schroedinger_SELF-CONSISTENT.png

022__Schroedinger_SELF-CONSISTENT.png
To discuss some of the features - we now develop a very simple
model for
basic features of such effevtive potentials (self-consistent
potentials, fields)
030_Screened_chsrge_atom_model_Ni_noble_gas.png

030_Screened_chsrge_atom_model_Ni_noble_gas.png
Here we have found out that nickel
Ni Z=28 should be a noble gas
So why is it not?
040_Coulomb_potential_degenerate_screened_E_nl.png

040_Coulomb_potential_degenerate_screened_E_nl.png
En becomes Enl - i.e. the energies
are different for differing values of the orbital momentum number l
Here are the experimental values to be discussed
050_Noble_gases_Ionization_pot_Configurations.png
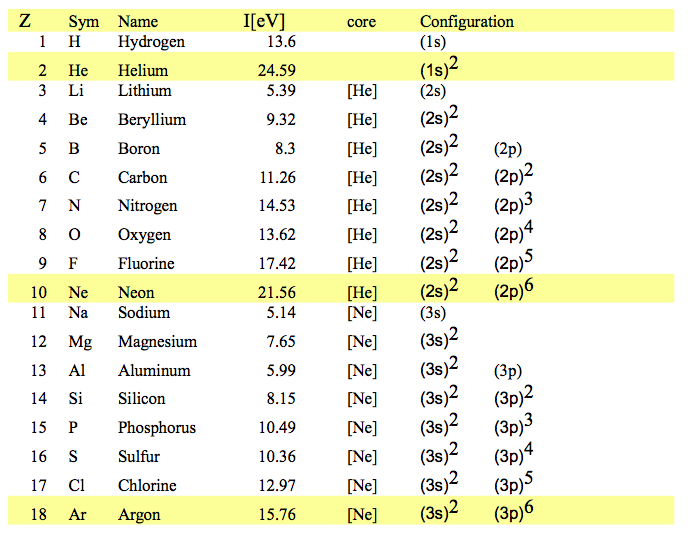
050_Noble_gases_Ionization_pot_Configurations.png
053_Noble_gases_Ionization_pot_Configurations.png
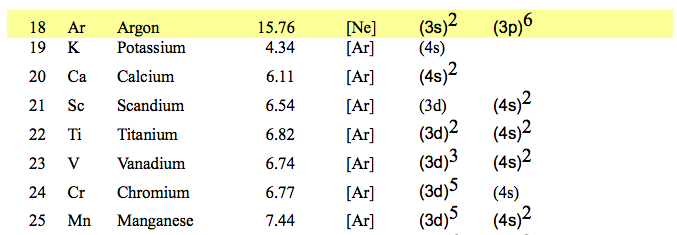
053_Noble_gases_Ionization_pot_Configurations.png
056_Noble_gases_Ionization_pot_Configurations.png

056_Noble_gases_Ionization_pot_Configurations.png