Interaction of Atoms with Light - Part 2
The PDF-file of the presentation : Light_Atom-2013.10.16.pdf
This lecture :
- Decaying states - transitions -
exponential decay - natural line width
- PART II - The Physics of
Fields - Eigenmodes of systems with many degrees of freedom
Systems with many degrees of freedom (infinitely many - continuous
systems)
Revisiting the 2-well problem - first discussing the two "new"
stationary states - i.e. how
the state in the isolated single well becomes slightly split two states.
Then - the relevance. This is the basis of molecular binding.
Further, such two states (or analogous ones, rather) are found for the
ammonia molecule
and they are the basis of the historically important ammonia maser
(
http://en.wikipedia.org/wiki/Maser#History
)
An interesting story can be found at http://laserstars.org/history/
especially
http://laserstars.org/history/ammonia.html
010_two-level-comment.png

010_two-level-comment.png
From the golden rule
golden-rule-summary_____w.png

we can try to see what is the probability of NOT DECAYING as a function
of time.
We derive quickly a negative probability.
So this must be modified, the probability to decay is proportianal to
the probability that it has not decayed YET.
Thus we get a new differential equation and thus the
EXPONENTIAL DECAY law.
015_from_delta_to_width_perturbation.png

015_from_delta_to_width_perturbation.png
And we must go back to the derivation leading to the "delta-function"
in energy
golden-rule-summary_____w.png

Because of the exponential decrease of the initial coefficient we must
modify the (framed to the right) equation
( square root of probability, i.e. negative exponential of w/2 )
016_Line_width_from_exponential_Decay.png

016_Line_width_from_exponential_Decay.png
Lorentz shape - the linewidth - derived - This can also be used
in discussions of
"time - energy uncertainety" - which is often misinterpreted.
The outlined relation between "lifetime" 1/w and Gamma is the
natural interpretation
The Lorentz shape - natural
linewidth
018_Line_width_from_exponential_Decay.png
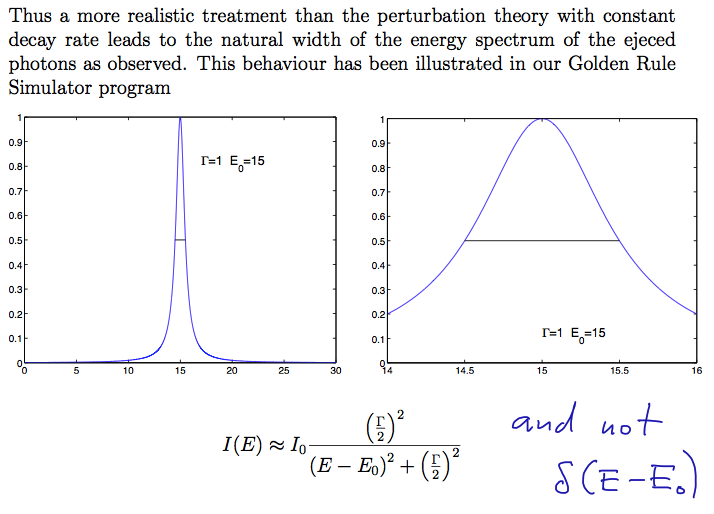
018_Line_width_from_exponential_Decay.png
The
Lorentz shape - natural
linewidth - Line shape is not a "line" as
delta-function
Line widths in experiment:
All decaying states behave in such way - they are unstable states, i.e.
not stationary,
i.e. not EIGENSTATES of energy of the whole relevant system.
--- In our case the "whole relevant system" is the atom + the field
--- generally, all elementary paricles are observed as unstable states
--- nuclear excited states, radioactive nuclei .... etc
Natural linewidths (Lorentz type) and other processes, experimental
resolution etc - mainly Gaussian shape
Lorentz Shape, Gaussian Shape - and illustration of
Voigt's line
(all on a logaritmic scale)
020-Line_widths-natural_and_broadening.png

020-Line_widths-natural_and_broadening.png
Line Shapes are important in many fields of science; Spectroscopy,
Astrophysics, Plasma Physics
PART II - The Physics of Fields
-
Systems with many degrees of freedom
(infinitely many - continuous systems)
Systems with "harmonic vibrations" - the potential energy quadratic form
All such systems can be found to have independent harmonic eigenmodes
Finding eigenmodes, eigenfrequencies == finding normal coordinates
We show here that it all can be accomplished by linear algebra -
eigenvalues and eigenvectors
101_coupled_oscillations.png

101_coupled_oscillations.png
Diagonalization - connection to eigenvectors
110_diagonalize.png

110_diagonalize.png
By these linear transformations
one finds decomposition into non-interacting (de-coupled)
oscillations - called -
eigenmodes
or
normal modes
120_Normal_coordinates_decoupled_oscillators.png

120_Normal_coordinates_decoupled_oscillators.png
Example of finding normal coordinates for strong of coupled
spring-ball oscillations
200_string_of_balls_with_springs.png

200_string_of_balls_with_springs.png
The normal mode - individual displacements u in terms
of a given k-th normal coordinate
i.e. k-th normal mode
210_string_of_balls_with_springs.png

210_string_of_balls_with_springs.png
The matrix V for a coupled system with transformed equal mass m=1
and spring constant k=1
Eigenvectors of the above matrix for various N, N=20 and N=100
220_string_of_balls_EIGENVECTORS.png
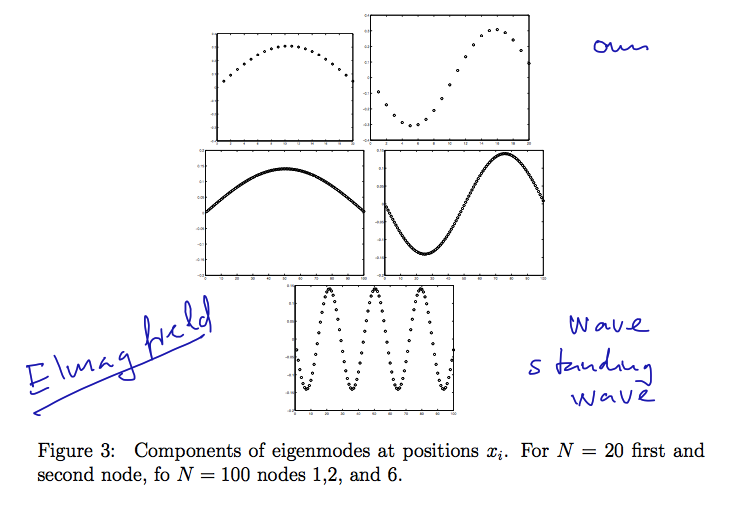
220_string_of_balls_EIGENVECTORS.png
Those are the eigenmodes, ressembling the vibration modes of a string
(standing waves)
No node - fundamental mode, one octave higher - one node, and higher
harmonics ....
.... see e.g. http://www.phys.unsw.edu.au/jw/strings.html#modes
or http://en.wikipedia.org/wiki/Normal_mode#Coupled_oscillators
Next topic: Quantum description of harmonic oscillators - Phonons and Photons












