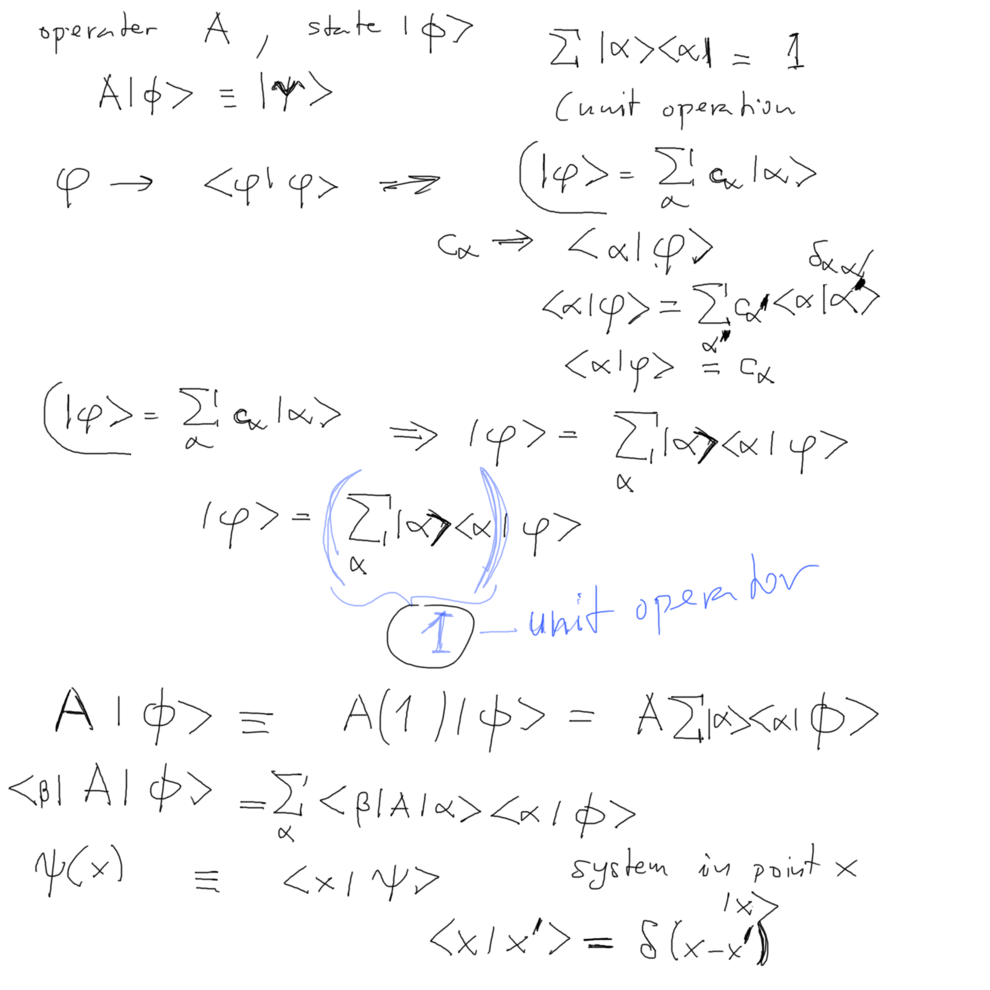Many Electron Atoms Part 4
Content:
Details of the Hartree-Fock equations derivation
Non-local nature of the exchange potential
Meaning of the orbital energies
We started by the
Overview of Hartree - Fock equation derivation - clipped and glued into
the first slide (0000_Hartree-Fock-Preview.png)
:
1. the functional - expectation value of total energy -
single particle and pair contributions
2. Lagrange multipliers - including the normaliztion
condition of the orbitals (N various orbitals )
3. "Variation" must be zero, for arbitrary variations of
each orbital
==> each remaining integrand (in Dirac notation, remove
the < and the variation ) must be zero
==> N independent equations
4. ... for illustration - we gave the results "for
Hartree", i.e. when only direct term present
5. The Hartree-Fock equations are derived
- with the direct (Hartree) term and a sort of exchange term
In the following, we look at various steps in the derivation
0000_Hartree-Fock-Preview.png
 0000_Hartree-Fock-Preview.png
0000_Hartree-Fock-Preview.png
First, we revisit the variational "derivation" of Schrödinger
equation
( i.e. revisit the requirements and operations which from
a stationary value condition for a certain functional
lead to
Schrödinger equation )
This is written in Dirac notation and below in coordinate form
Further we look at comparison of "at minimum differential is equal to
zero" with "variation is equal to zero"
Finally, we discuss the case when the functional contains two
integrations, as in our many-electron
energy expression ( the pair interaction operators)
Note that all this is needed in the procedure outlined in the first
slide (0000_Hartree-Fock-Preview.png
)
0010_Schrodinger_from_variation_TO_many_electron_case.png

0010_Schrodinger_from_variation_TO_many_electron_case.png
Just above, we discuss the case when the functional contains two
integrations, as in our many-electron
energy expression ( the pair interaction operators; the single particle
terms are easier)
Note that all this is needed in the procedure outlined in the first
slide (0000_Hartree-Fock-Preview.png
)
the pair interaction operators are looked at once more in more
detail
(the single particle terms are much easier)
0020_reducing_the_variation_is_zero_conditions.png

0020_reducing_the_variation_is_zero_conditions.png
Overview of Hartree - Fock
equation derivation - once more,
this time with stress on the original
summation over orbitals ( note the differences
from the first slide 0000_Hartree-Fock-Preview.png
)
Thu summations - over alpha - are made visible by blue-background )
0023_reducing_terms.png

0023_reducing_terms.png
When the compact Dirac notation is written out in terms of integrals
Direct term potential (Hartree) vs
Exchange potential
0026_direct_exchange_detailed_integrals.png

0026_direct_exchange_detailed_integrals.png
When the compact Dirac notation is written out in terms of integrals
Direct term potential (Hartree)
vs Exchange potential
(original snapshot, without notes)
0030_resulting_direct_and_exchange_terms.png

0030_resulting_direct_and_exchange_terms.png
The exchange
potential is a NON-LOCAL OPERATOR
In order to understand non-local operators, we must understand when a
potential is a local operator ....
Relation of Dirac notation and the
"wavefunction" - as a projection of a state vector on the
position eigenstate
Delta-function scalar products etc....
0040_completness_unit_operation_expansions.png
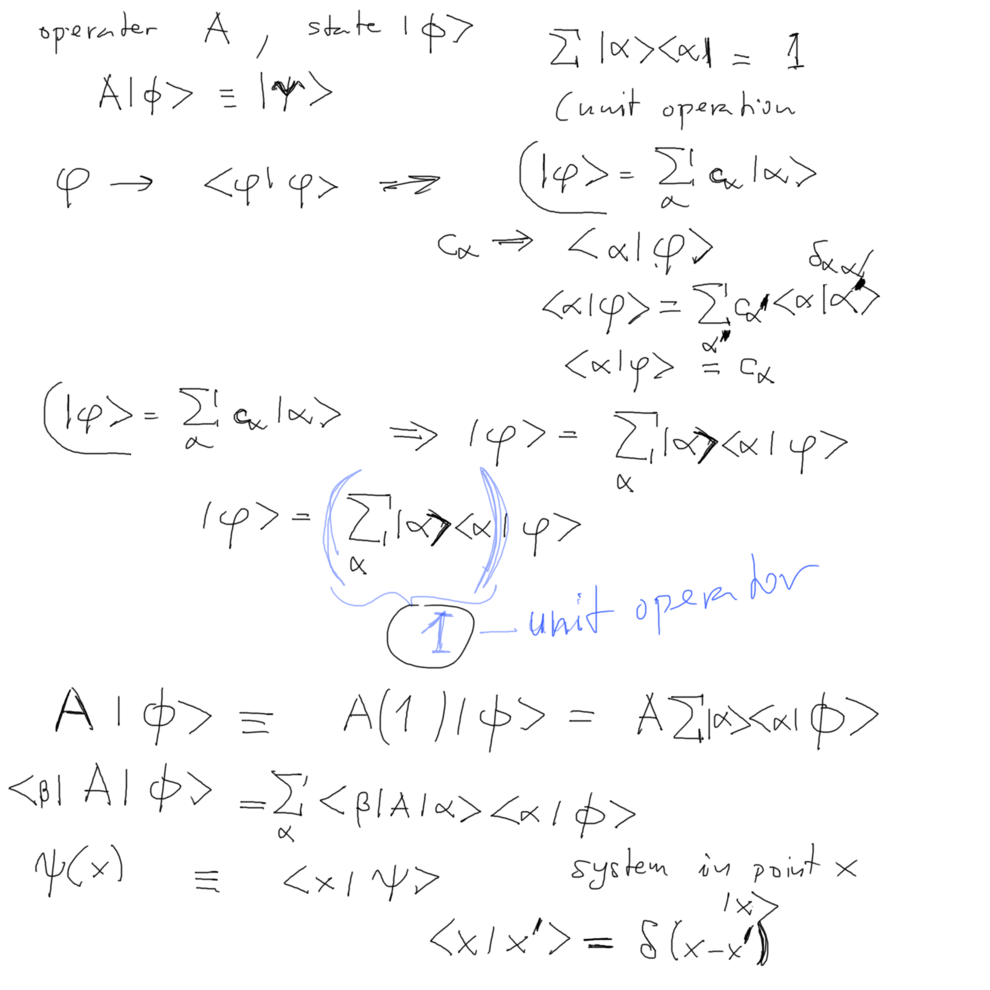
0040_completness_unit_operation_expansions.png
continue ....
In order to understand non-local operators, we must understand when a
potential is a local operator ....
Relation of Dirac notation and the
"wavefunction" - as a projection of a state vector on the
position eigenstate
Delta-function scalar products etc....
non-local potentials ....
velocity-dependent potentials - see further
0050_state_vector_WAVE_FUNCTION.png

0050_state_vector_WAVE_FUNCTION.png
non-local potentials ....
velocity-dependent potentials
( mainly discussed in more complex systems, nuclear
models etc .... )
... we can understand some features by analogy with Green's
function
For the atomic physics case: The most important is
the practical feature:
The differential Schrödinger
equation
is replaced by a system of
integro-differential
equations Hartree - Fock
Integro - differential equations - approximative
methods - see next part below
0060_NON-LOCAL-OPERATORS--from-exchange.png

0060_NON-LOCAL-OPERATORS--from-exchange.png
Integro - differential equations - approximative
methods
The non-locality is simulated by various "corrections"
0070_Non-local_Hartree-Fock---Density_Functional.png

0070_Non-local_Hartree-Fock---Density_Functional.png
Density Functional Theory became a more
popular device for introducing the
SCF ( Self -Consistent - Fields )
http://en.wikipedia.org/wiki/Density_functional_theory
The non-locality - exchange - is built - in (simulated) in the Density
Functional Theory
excahange energy term of the functional ( and not derived
as here )
seethe section
http://en.wikipedia.org/wiki/Density_functional_theory#Approximations_.28exchange-correlation_functionals.29
( i.e. the section 3 Approximations
(exchange-correlation functionals) of the above
article)
How to understand the
"ORBITAL ENERGIES"
0080_Hartree_Fock_summing_orbital_energies.png

...
The last expression - the
expectation value of total
energy of the N electrons -
is the starting point of the variational
procedure which gave us the Hartree-Fock equations
0080_Hartree_Fock_summing_orbital_energies.png
How to understand the "ORBITAL
ENERGIES" ... continued
We consider all the N Hartree-Fock equations for the N orbitals;
For each of then we form the orbital's expectation value of the
equation - and we get a relation
for the value of the "orbital energy" ( epsilon - index -
alpha )
OK, we call thisof the orbital alpha
Then we make a sum of the
orbital energies
we obtain an expression which is
nearly the same
as the above
expression for the total
energy of
N electrons
but differs by the details of the summation ..... over
ordered pairs vs. just pairs
0085_summing_orbital_energies.png

0085_summing_orbital_energies.png
What is the difference
between the two summations?
0090_sum_of_orbital_energies_vs_total_energy.png

0090_sum_of_orbital_energies_vs_total_energy.png
The resulting observation is:
The sum over all occupied
orbitals energies gives the total energy of the system PLUS an
extra term
which is equal to the total of
pair interactions
or as written in the slide:
the total energy of the system
is equal to the sum over all occupied orbitals energies MINUS the
interaction
of the pairs
 0000_Hartree-Fock-Preview.png
0000_Hartree-Fock-Preview.png