Schrödinger equation is introduced usually in time dependent form, even with possibility of time-dependent total
energy (hamiltonian operator explicitely time dependent)
but then all this is quickly limited to time-independent hamiltonians which can then lead to stationary states.
Mathematically - this is shown by the possibility of sepeartion of time and space coordinates.
Next step is then often the postulate that "only eigenstates are possible outcomes of measurement", and only in
more advanced or complete courses we see some treatment of
time-dependent perturbation theory
Fermi Golden Rule - for decay rate of excited systems
Ramsey or Rabi oscillations
In this part of our course we thus first visit some simple systems, look at the time-dependent Schrödinger equation,
derive "Fermi Golden Rule" - for decay rate of excited systems, but concentrate specially on the natural line widths.
In many texts (even in scientific literature) the existence of natural line widths is ascribed to "energy-time Heisenberg
uncertainety relation.
We shall see how seriously we should take such statements.
We shall start by a simple treatment of a general time-dependent total hamiltonian
in a form often used to introduce time-dependent perturbation theory
BUT THEN QUICKLY TURN to time-independent case
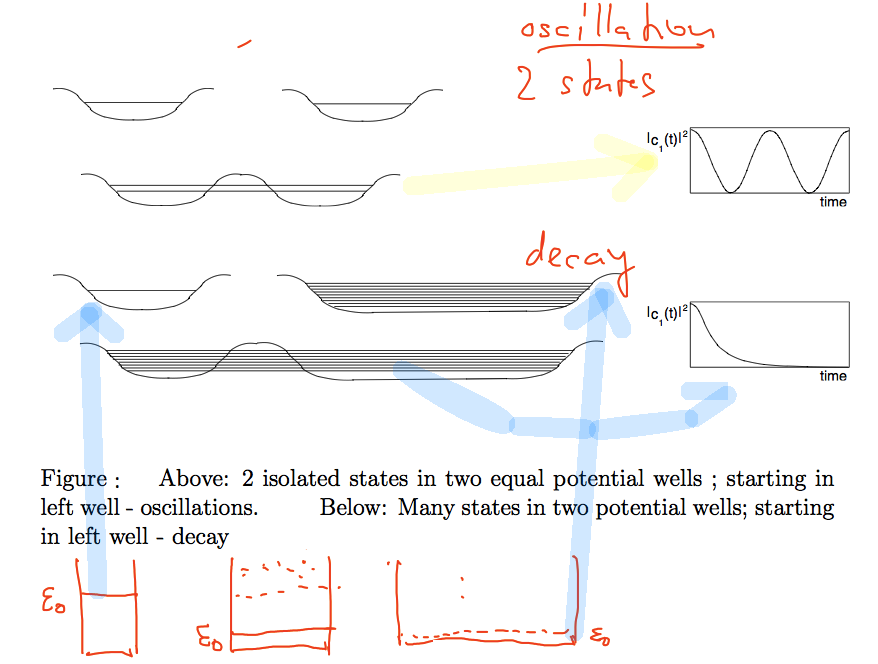
and further to a two-state problem - TWO identical potential wells
"competing" to keep bound one particle (think it to be an electron)
----- This story starts about in the middle of the plate:
Instead - --- for 2 levels H = H0 + V1 + V2

0000_TDSE_and_time-dep-time-indep_H.png
This continues in the description below.
We know that eigenstates of the whole H = H0 + V1 + V2 form a sort of split doublet (if the wells are moderately separated)
More details are below
Physics: the "electron" is placed in a state at t=0 confined to ONE WELL ONLY (1 well eigenstate)
The probability is seen to be OSCILLATING between the two wells
This is seen from the EIGENSTATES of the whole problem

0002_time_pict.png
oscillations can be seen e.g. in DOUBLE QUANTUM DOTS experiments ( performed in the last decades )
or indirectly in many atomic and molecular physics experiments

0004_time_pict.png

0006_time_pict.png
For a system which can be "localized" in two different regions by neglecting a certain interaction
- and by neglecting the interaction, we can isolate two "states" (here left or right well)
- the system has two energetically close eigenstates ( + and - )
these eigenstates are approximately given as sum (+) or difference of the "non-interacting" states
- when such systems is prepared in (or forced into) one of the isolated states (left or right well)
its probability to be detected in the "left" or "right" region will oscillate with time as shown
For this to be true, the two isolated states must have the same energy! (energy degenaracy)
.... then the interaction has removed the degeneracy, leads to two total eigenstates split by a small energy difference
and to the oscillation of the probability (this comes out without the necessity of obtaining any explicit solutions of
time-dependent Schrödinger equation - the knowledge of the energy splitting determines the oscillations
Further down is discussed a similar model - but one of the wells is much larger
- that means there are many many levels energetically close (nearly degenerate) with the
single level in the "left" well
.... Many states in two potential wells ....
this means there will be many states in the "large well" - plotted are only those which
have "a non-vanishing amplitude" of the single isolated left-well state
with a reasonable model for the "diagonalization" results - we obtain a (nearly)
exponential decay of the probability that the left well state remains populated
SO: for two states only - oscillations (probability comes back, oscillates)
for many states the probability can not "find way back" - we get the decay of the single state
BOTH CAN BE UNDERSTOOD IN TEMS OF EIGENSTATES of the total system
0007_time_pict-narrow-broad-well.png
( energy is proportional to typical "k" which is given by 1/a - "a" the size )
Next slide: Top - summary of above
Lower part: the matrix form of the model: the energies are equidistant, the interaction
is constant
we solve the time-dependent Schrödinger - in matrix form - for this model further down

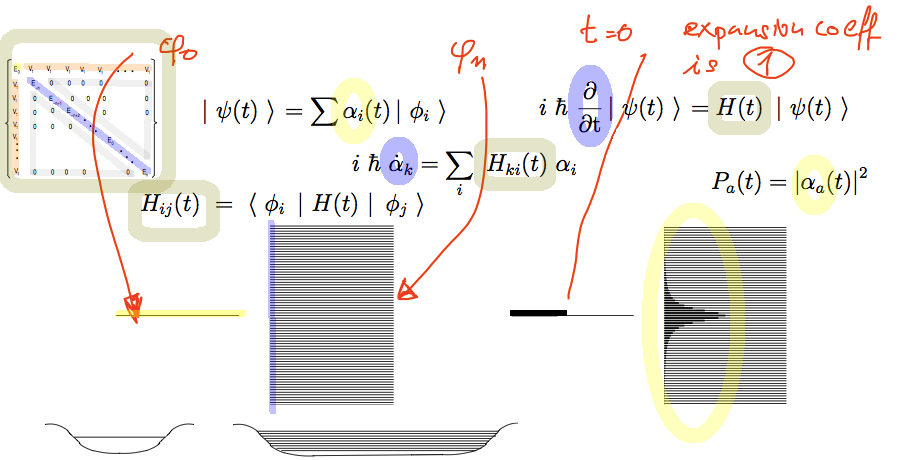
0010_Time_developement_Superposition_and_the_Simulator.png
the matrix form of the model: the energies are equidistant, the interaction is constant but only 1 row/column
When the matrix is diagonalized - the projection of eigenstates on the isolated state (left single line)
are the circles
the lines show the projection of the time dependent solution
on the quasicontinuum states with that energy
picture from Matlab Golden Rule simulator
we solve the time-dependent Schrödinger - in matrix form - for this model further down
Golden Rule simulator ( in matlab or in the browser - javascript )
0032_TDSE_decay_model_elements.png

0061_TDSE_approach_MATLAB.png
0062_TDSE_approach_MATLAB.png
0063_TDSE_approach_MATLAB.png
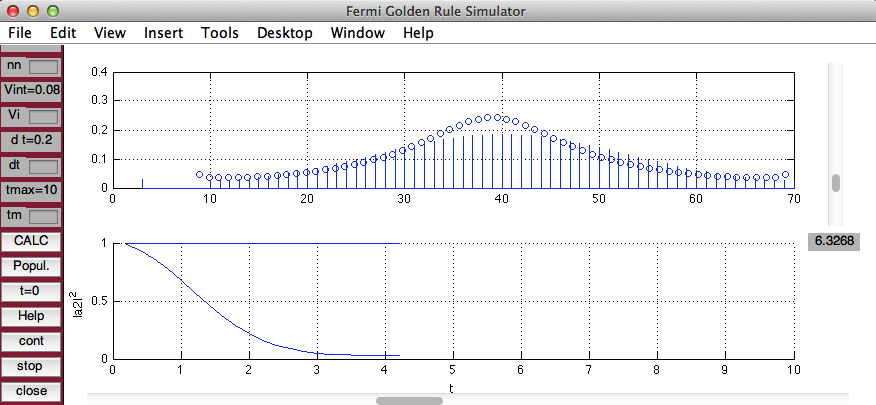
Browser program - Fermi Golden Rule SImulator http://web.ift.uib.no/AMOS/golden/
40 states in quasicontinuum
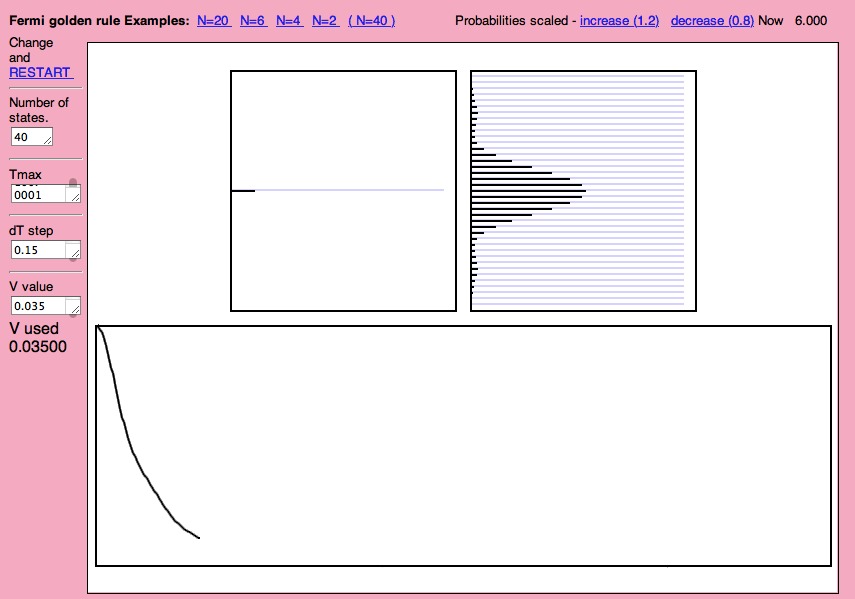
1001_webpage.png
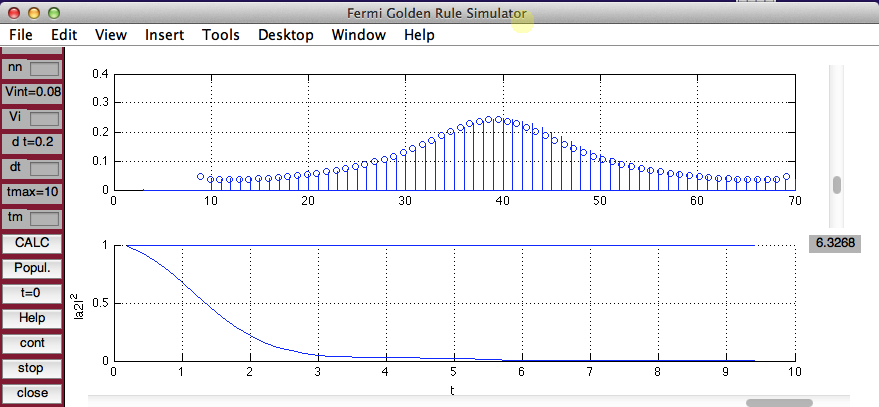
Browser program - Fermi Golden Rule SImulator http://web.ift.uib.no/AMOS/golden/
1 states in each region (not really a quasicontinuum ... ) but the program runs.
Exercise: try N=2 N=4 N=6 .......
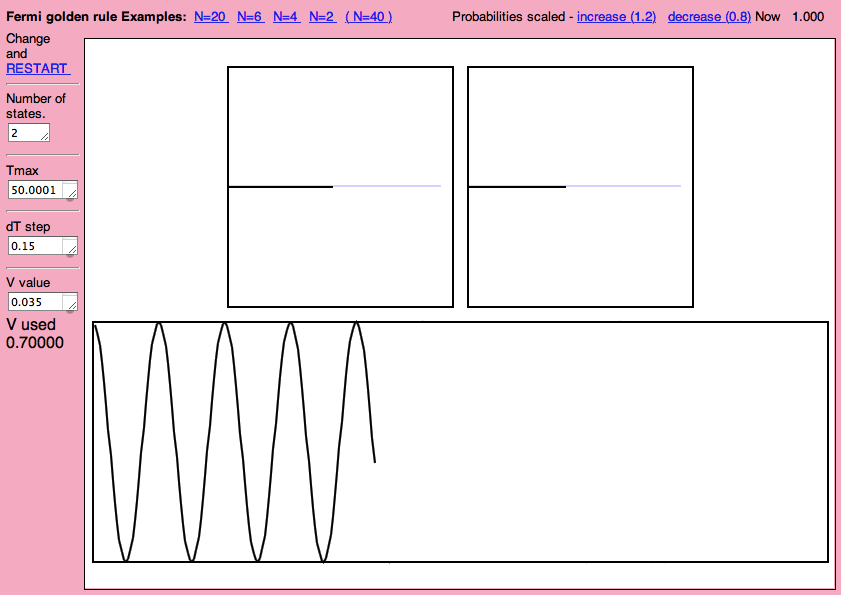
1002_webpage_2_levels.png

0035_TDSE_approach.png

0036_TDSE_approach.png

0037_TDSE_approach-no_timedep.png

0038_TDSE_approach.png

0039_TDSE_approach-DECOUPLE_EQU.png
Time independent
uncoupled and the unknown c is known -> 1

0040_TDSE_approach.png

0041_TDSE_decoupled_solved.png
We shall SUM OVER THE FINAL STATES to find out how much probabilty "runs away"
We shall do it for large times - how then does the F (above) appear as function of omega (energy) ?
Next lecture - approching the delta - function
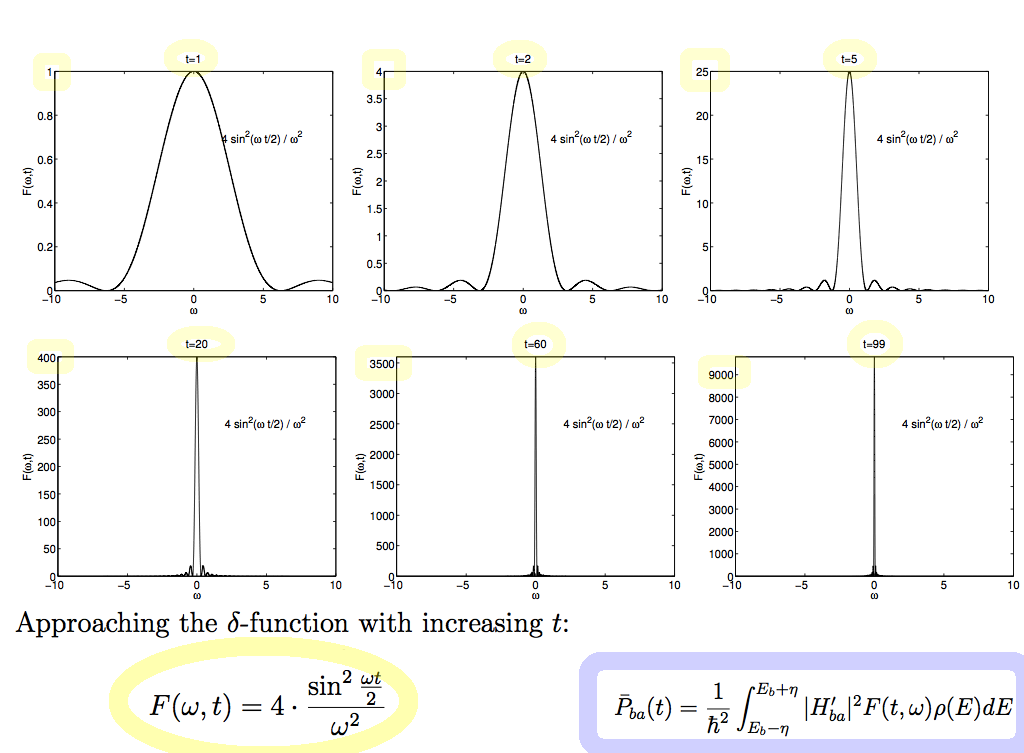
0045_TDSE_decoupled_Integral_Delt_function.png
Does the delta in energy really mean energy conservation?
NATURAL LINE-WIDTH VS ENERGY CONSERVATION
Other systems, not only "electrons in wells"; PHOTON FIELD
What are the quantum states of force fields?