Light_Atom-MARKING_2014_11_04.pdf
the parts on
Dirac delta-function
Fermi Golden Rule
Constant rate and exponent. decay
Line width from exponential decay
Density of States
Eigenmodes for coupled vibrations.
The time-dependent Schrödinger equation - after expansion in eigenstates of a certain H0 - in matrix form
This implies dividing H into two parts
H = H0 + H' (t)
This can be transformed by changing the coefficients (or effectively the basis states)
For the new definition - the H0 cancels and the resulting system of equations
contains only the matrix elements of H' (t)

0000_substitutions_mod.png
contains only the matrix elements of H' (t)
Decoupling of the system of coupled equations:
the "perturbation assumption" - that for the approximation the expansion coefficients on the right hand side of the equation
are set to 1,0,0,0,0
reduces the matrix effectively just to column vector = column vector which means that
this vector equation can be instead written as eqality of each component - separately

0001_decoupling_mod.png
UNCOUPLED Further, they are of such type - that they can be simply integrated

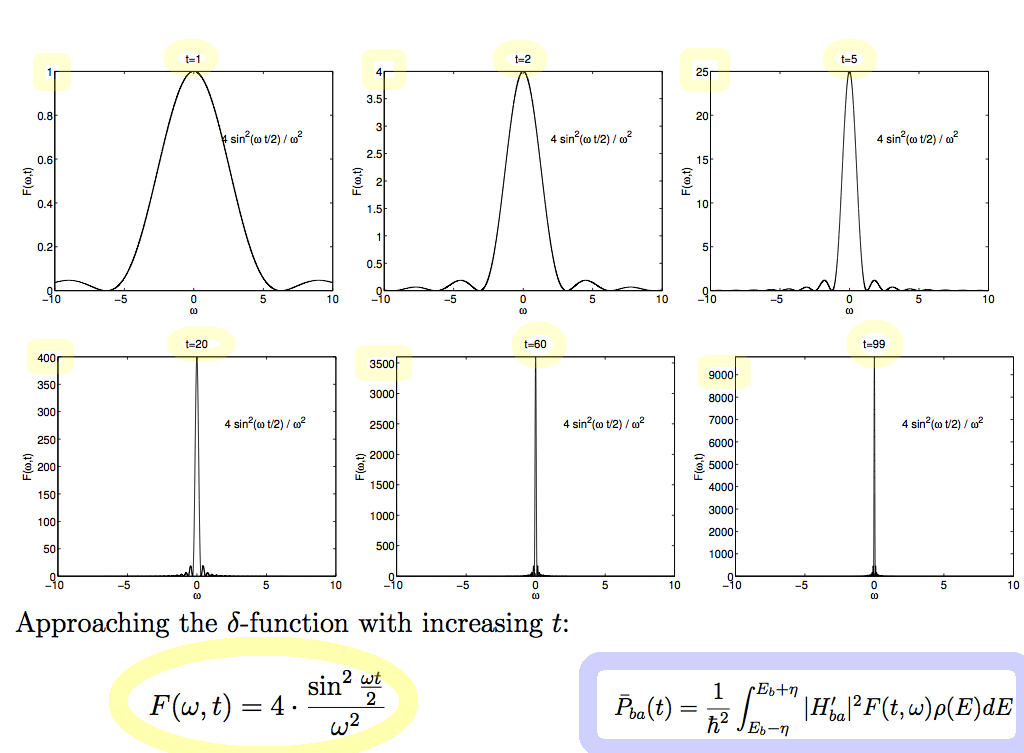
WHY INTEGRATE OVER THE ENERGIES? ( over omega) - sum over the state in "the continuum - see below

0009_integrate_over_states.png
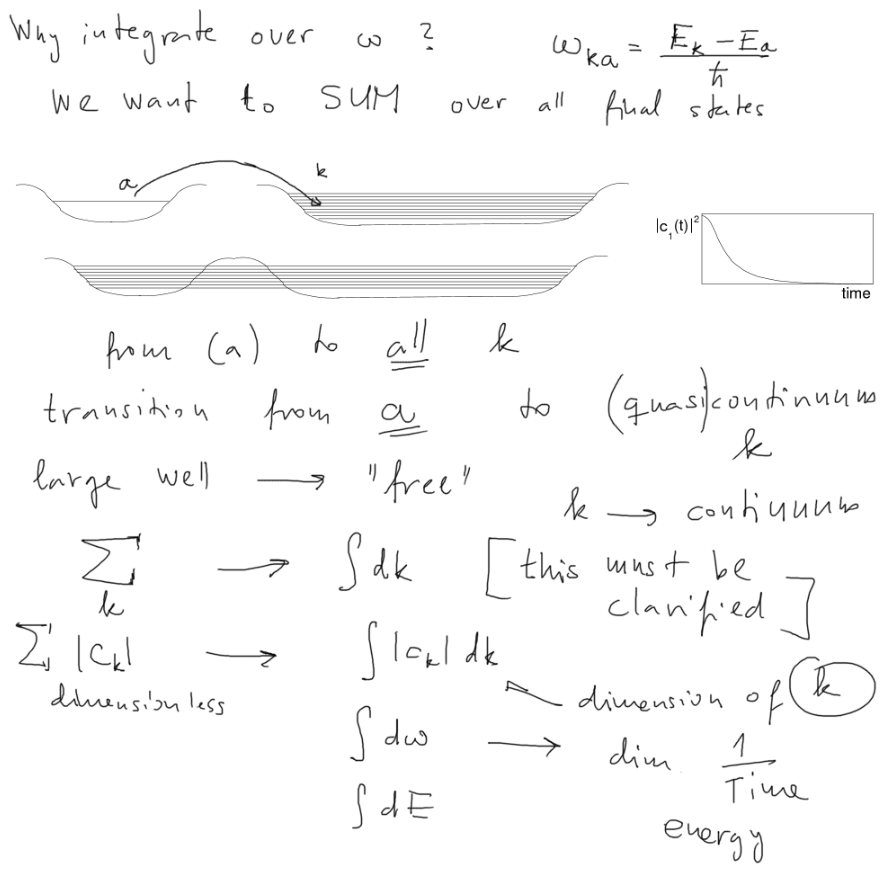
0010_integrate_omega.png
A more detailed treatment of this will come when we consider REALISTIC case of plane waves (for photons)
BELOW: Towards the Golden Rule
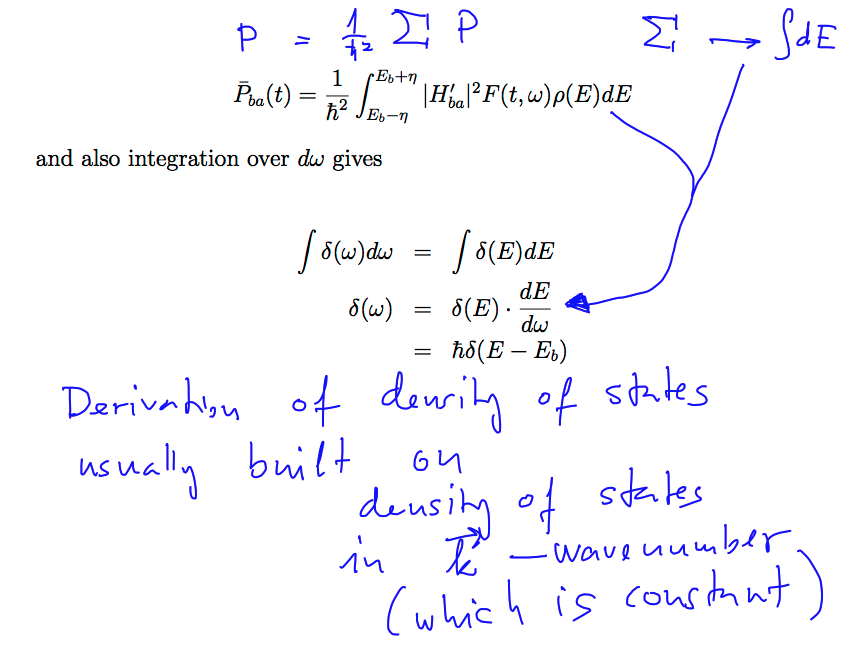
0014_delta_and_density_of_states.png
It is called Fermi's golden rule, because Enrico Fermi gave famous lectures on quantum mechanics and he called
this result a "golden rule" of quantum mechanics. ( the actual first derivation reportedly first appeared in
one paper by Wentzel)
Note the time square dependence - to make the delta-function application we need one of the powers of time
Then the probability of integrated probability of occupation of the final states is proportional with time
Instead of it, we take the CHANGE - the RATE of change, i.e. the time derivative to get the final "rule"
The rate of change of the probability is then constant with time

0021_Fermi_Golden_Rule.png
The "golden rule" thus implies a sharp (delta-function-like in energy) emission spectrum.
Further we shall look at how this must be modified
... to account fo the natural line width
Next slide:
Here we address first time the question - what has our model with two potential wells to do with light emission?
Not much. But as we see, what is important is the fact of "quasicontinuum" or simply continuum of energies.
So as far as the system in question has this property:
1 special discrete energy state (degenerate - close to) many states with "continuum" energy
the derivations will remain valid
Here is shown the atom + field system schematically
Bottom part - Then we make the first mention of how to approach the natural line width - by including the exponential
decay - more detail below
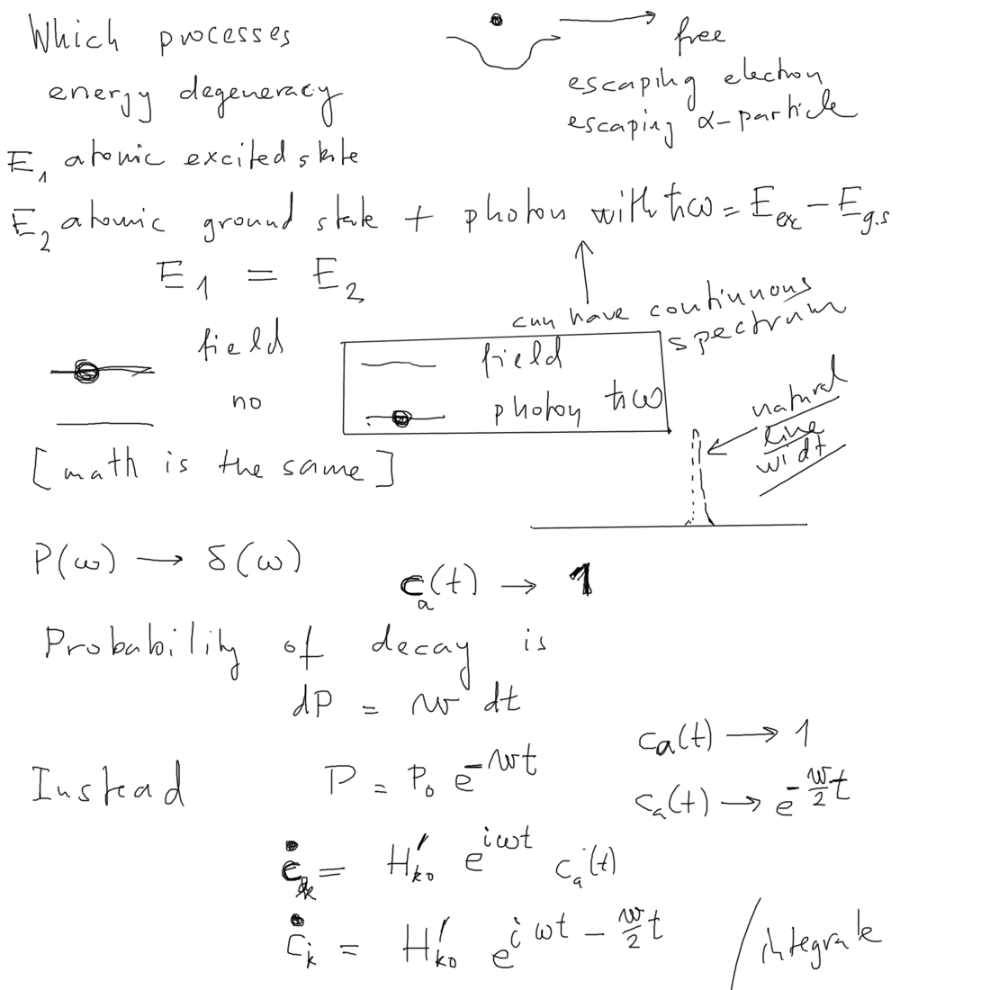
0020_decays.png
decay - more detail below
One more illustration of the actual system the atom + field system schematically
( instead of our model with two potential wellswhich we used for introduction)
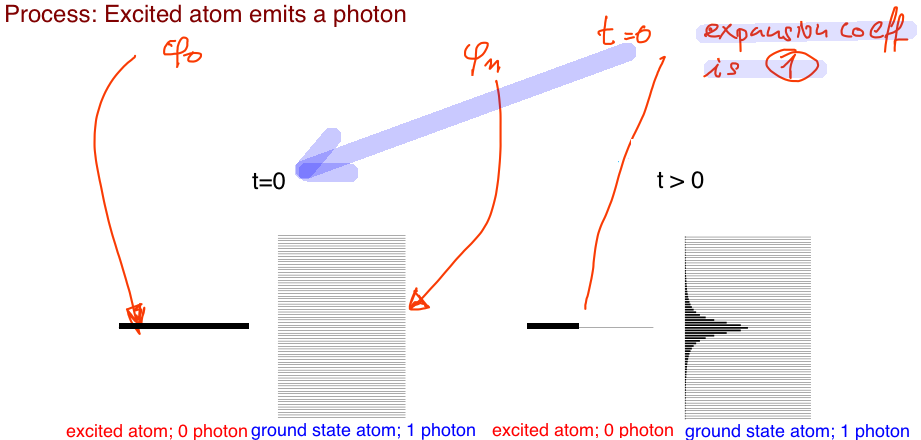
0022_decay_excited_state_atom_deexcites_emits_photon.png
initial state excited atom no photon final state de-excited atom one photon with energy close to hbar omega
NEXT
Here follows the discussion in detail:
How to get from the perturbation derivation - leading to constant decay rate
(but implying delta-function-like spectrum)
to the realistic case - and natural line width

0025_constant_rate_exponential_decay.png
of the initial state is kept equql to one.
That naturally can not be exactly true, since the probability to remain in this state decreases with constant
rate - so the ( absolute value of ) the coefficient must INSTEAD of 1 behave as exponentially decaying
(with square root ---> 1/2 of the decay const. )

0030_Line_width_from_constant_rate.png
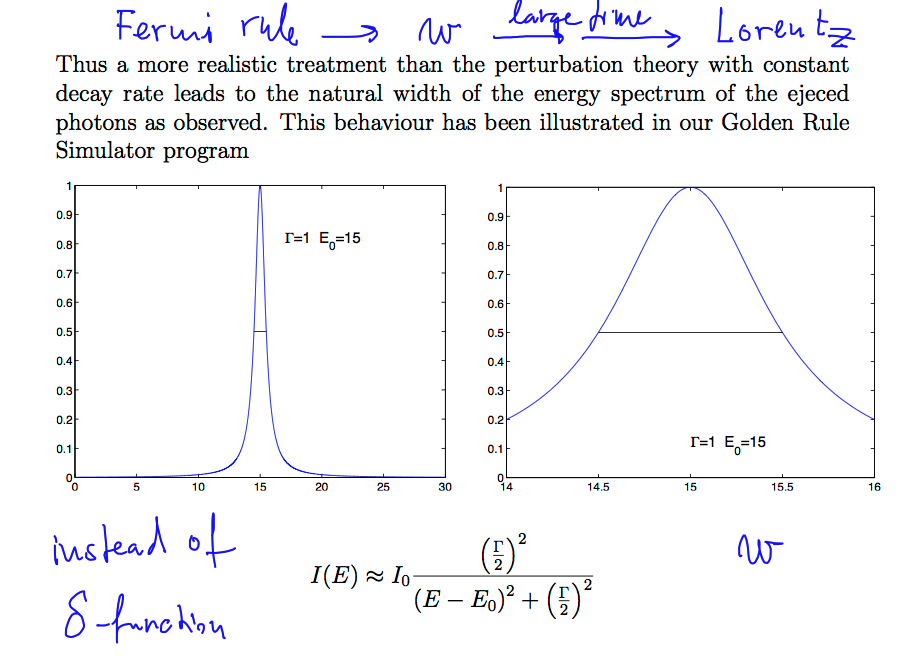
instead they get the so called Lorenz shape.
NOTE: it is the same simple time integration, but now including the (square root) of exponential decaying population

0033_Line_width_from_constant_rate.png
NOTE: this ressembles the resonance in damped driven oscillator
0040_Natural_Line_Shape_energy_distr.png
Atom interacting with a field (atomic states known already)
We need to describe
Quantum states of the field
Interaction between the field and the atom
Electromagnetic field is clearly an "extended system"
If the field is to be known, it must be known in every point in space
--- imagine that we can "discretize the space" - divide it into small boxes
--- Then Maxwell's equations describe how oscillation in (or the general state of) one such "box"
is connected to the oscillation in (or the general state of)the neighbouring box(es).
So we start by considering a system of harmonic oscillators - which are coupled
First model - balls connected by springs

0050_VIBRATIONS___Eigenmodes_normal_modes.png
( x a - x b )2 = x2a + x2b - x a x b - x a x b is exactly of the form V in the above - symmetric matrix V
Below we show a series of transformations which leads to re-writing as a sum
of independent oscillations ( with unit mass )

0055_VIBRATIONS___Eigenmodes_normal_modes.png

0060_Eigenmodes_normal_modes.png
Eigenmodes of a string of balls connected by strings (in 1 dimension; balls would
be attached on a wire or confined in a tube, to realize this math)

0070_Eigenmodes_normal_modes.png
Eigenmodes of a string of balls connected by strings (in 1 dimension; balls would
be attached on a wire or confined in a tube, to realize this math)
The "local amplitudes" - i.e. displacements of each ball - are plotted as y-coordinate
--- though they are naturally displacements in the "x-direction" - one-dimensional
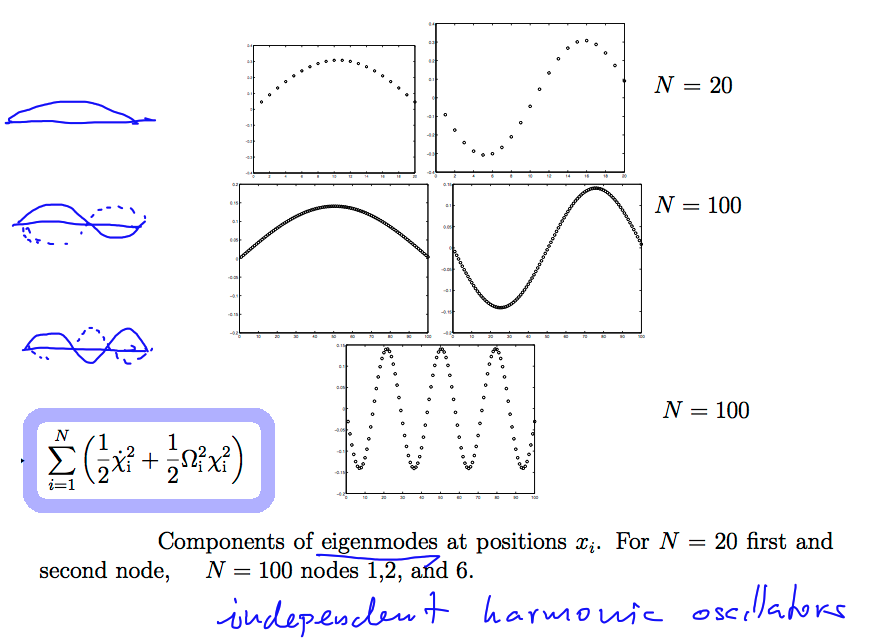
0080_normal_modes_strings.png
can be treated as collection of independent oscillators
We need to describe further (next lecture)
Quantum states of the field
Interaction between the field and the atom
Electromagnetic field is clearly an "extended system", wave-like; what are the eigenmodes ?
And what are the photons?