to index              2014_11_04 Previous Lecture Note             LECTURE NOTE   2014_11_06           2014_11_20 next lecture note

charge_in_elmag_marked-2014.11.06.pdf     is an extra text  on  Charged Particles In an Elmag. Field       Extra on                                    CHARGED PARTICLE IN TIME-DEPENDENT  ELECTRO-MAGNETIC FIELD Light_Atom-marked-2014.11.06.pdf        Is the presentation with handwritten lecture comments and markings                                                                 Most of these are captured (and edited) below and commented further This is roughly the structure of the index page which we touched in this lecture - see the capture just below

See also generally:       ../2013_10_29/index.html       Last year's lectures Eigenmodes for coupled vibrations. (last lecture) see also 2013 lectures ../2013_10_29/index.html Algebraic Method for Harm. Osc. (see the notes!) Quant. th. of extended systems - fields Electromagnetic fields The Quant Th. of Elmag. Field Density of States Charged Particles In an Elmag. Field charge_in_elmag_marked-2014.11.06.pdf The Hamiltonian of Interaction Emission of Radiation by Excited Atom    (see already the last lecture)     see also  http://web.ift.uib.no/~ladi/Fysisk/Teori/Pictures/Golden.html The matrix element reduction Dipole Approximation Detailed Evaluation of Emission rate

The above table is roughly the structure of the index page which we touched in this lecture - see the capture just below

0000_notes-plan.png        0000_notes-plan.png

Extra on                                    CHARGED PARTICLE IN TIME-DEPENDENT  ELECTRO-MAGNETIC FIELD charge_in_elmag_marked-2014.11.06.pdf

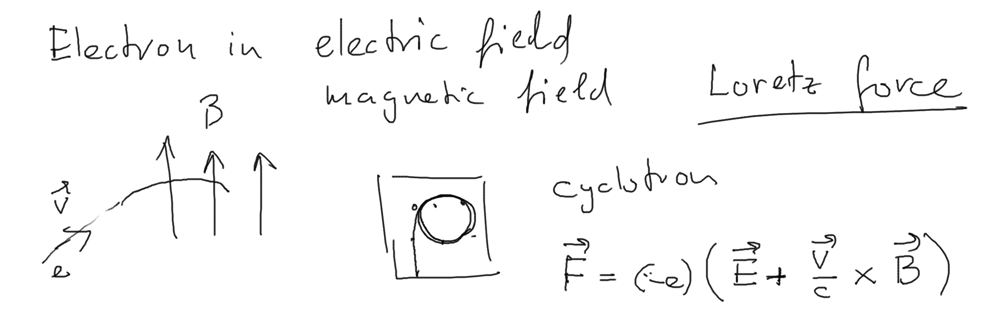
0010_Lorentz_Force.png        0010_Lorentz_Force.png

charge_in_elmag_marked-2014.11.06.pdf

0020_Lagrange_for_elmag_to_hamilton_1.png        0020_Lagrange_for_elmag_to_hamilton_1.png

All these are from charge_in_elmag_marked-2014.11.06.pdf

0030_Lagrange_for_elmag_to_hamilton.png                                             0030_Lagrange_for_elmag_to_hamilton.png

THE ABOVE - extra on      CHARGED PARTICLE IN TIME-DEPENDENT  ELECTRO-MAGNETIC FIELD

How to quantize the fields - find the EIGENMODES Each  EIGENMODE   - independent HARMONIC OSCILLATOR Each oscillator its CREATION and ANNIHILATION of QUANTUM                           - Eigenmodes for coupled vibrations. (last lecture ../2014_11_04/index.html)                           see also 2013 lectures                            ../2013_10_29/index.html                                                                        Algebraic Method for Harm. Oscillator              in the notes

algebraic_HO_010.png        algebraic_HO_010.png

Just by rewriting - in terms of DIMENSIONLESS  P,Q    -  we  get easy way  to    operators (just algebra)   a, a+

algebraic_HO_020.png        algebraic_HO_020.png

working with commutators   -  NUMBER OPERATOR     --   simply a combination    N  =  a+ a            what  are the properties of this operator?      Apply  it  -  it then gives the "number of quanta"

algebraic_HO_030.png        algebraic_HO_030.png

number of quanta      ---     LADDER OPERATORS   uppwards   a+     and   downwards     a         ----    N  =  a+ a

algebraic_HO_040.png        algebraic_HO_040.png

The states of the H.O.   -  or of the MODE of vibration ( wave)     Different numbers of quanta     Ground state - zero quanta present

algebraic_HO_050_Creation_annihilation.png        algebraic_HO_050_Creation_annihilation.png

QUANTIZATION OF ELECTROMAGNETIC FIELD       The energy expression   -   two ways       (EQ. 41  -  and the next slide )       A operator expressed in eigenmodes'  creation and anninilation operators

E001_vector_pot_operator_ELMAG_field.png        E001_vector_pot_operator_ELMAG_field.png

WHAT DETERMINES THE CONSTANT ABOVE ??    SEE NEXT SLIDE

E010_determine_constant_fact_ELMAG.png        E010_determine_constant_fact_ELMAG.png

STATES OF THE FIELD   -   in terms of quanta of eigenmodes

E011.png        E011.png

DENSITY of states

E015_Density_of_states.png        E015_Density_of_states.png

----

E018_Density_of_states.png        E018_Density_of_states.png

SEE THE GENERAL PART IN THE START                                                                                  (additional background note            charge_in_elmag_m arked-2014.11.06.pdf     )

E020_charge_field_interaction.png        E020_charge_field_interaction.png

DIPOLE APPROXIMATION

F_005_Dipole_approximation.png        F_005_Dipole_approximation.png

DIPOLE APPROXIMATION      both  removes the  wave-like factor  and  replaces "velocity"  by position  - dipole

F_008_Dipole_approximation_R-M.E..png        F_008_Dipole_approximation_R-M.E..png

above "drawing"   -  position  - dipole - illustration      induced dipole  story  ( electric field 'polarizes' atoms; induced dipole - position of the electron  )       FINAL APPLICATION OF FERMI's GOLDEN RULE

F_010_Emission.png         F_010_Emission.png

INSERTED   the interaction   atom - field  (electron - field )

F_020_Emission.png        F_020_Emission.png

insert density of states result, constants

G_010-evaluation.png        G_010-evaluation.png

THE OVER ALL STRUCTUR OF THE  MATRIX ELEMENT

G_020-evaluation_MATRIX_ELEMENT.png        G_020-evaluation_MATRIX_ELEMENT.png

EMISSION  IS DIFFERENT IN DIFFERENT DIRECTIONS     ( THE DIPOLE VECTOR  )                               NOTE THE ANGULAR  INTEGRATION  -  AVERAGING    one  slide further down

G_030-evaluation_with_anles.png        G_030-evaluation_with_anles.png

NOTE THE ANGULAR  INTEGRATION  -  AVERAGING

G_040-evaluation_final.png        G_040-evaluation_final.png

The final result -  HOW DOES IT SCALE     with the atomic number  Z

to index              2014_11_04 Previous Lecture Note             LECTURE NOTE   2014_11_06           2014_11_20 next lecture note