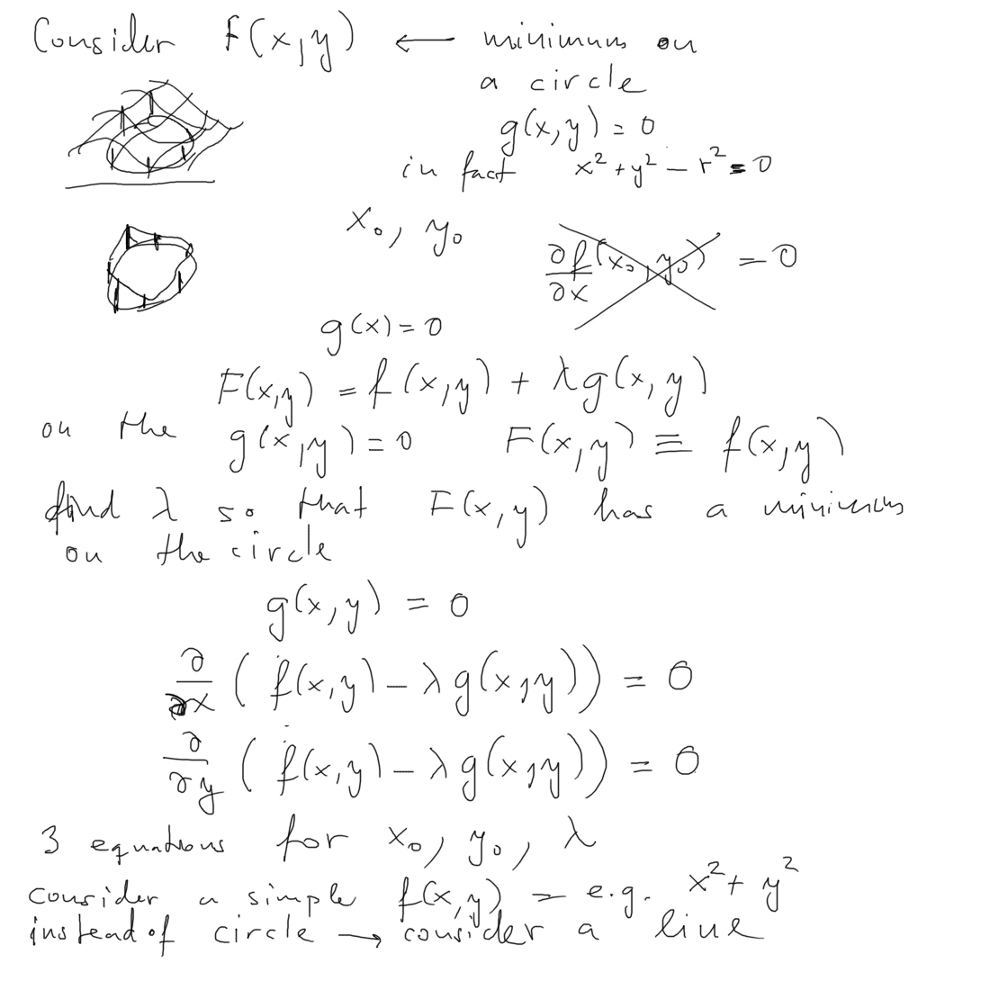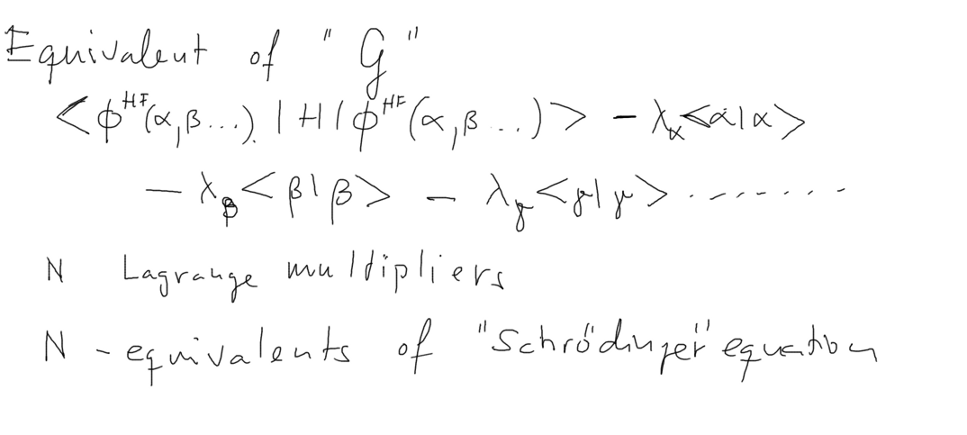Many Electron Atoms - part 3
Last time we have counted the non-zero terms.
The following slide is a combination of equations showing well how to
count.
1. First we do it for the single-term product function
there are N terms for the SINGLE PARTICLE
operators ( - i.e. sum over orbitals, because each
coordinate
sits in
its orbital )
and there are N(N-1) / 2 terms for
TWO PARTICLE - PAIR OPERATORS - by the same argument
2. Making the step to Slater determinants - on each side there are
N! terms, so the number gets enormous
But as in the case of normalization, only same terms
on both sides are nonzero -
THUS ONLY N! terms remain nonzero
- and they are identical in all respects - THIS CANCELLED
by normalization
3. Slater determinants and PAIR OPERATORS - it is
basically the same argument, but now we must consider
the two particles which interact - the
REMAINING N-2
orbitals on left and right side must be the same
thus also the two interacting must be the same
orbitals. But they can be swapped or not swapped - thus
two terms - not-swapped is called direct
term - swapped gets minus and is called the
exchange term
0010_evaluated_expectation_value_of_H_.png

0010_evaluated_expectation_value_of_H_.png
Thus this is the total energy - expectation value - Similar to the
He-case where its analogue has been
used as starting point for Variational Method
To be able to continue - we must establish a method
HOW TO RE_OBTAIN SCHRÖDINGER EQUATION using a
variational method, or rather a "variational principle"
This "principle" will be to find a suitable Functional -
and then finding a function which MINIMIZES that functional
will lead to the desired equation ( we get to this point below - see
the conclusion and come back )
Background concepts in encyclopedic way: what is a functional
see http://en.wikipedia.org/wiki/Functional_(mathematics)
Functional derivative http://en.wikipedia.org/wiki/Functional_derivative
also http://en.wikipedia.org/wiki/Functional_analysis
and http://en.wikipedia.org/wiki/History_of_variational_principles_in_physics
( Caution: some of these Wikipedia entries might be a bit "personal",
like e.g. the function
now in 2014 )
0020_How_to_Schroedinger_from_Variation.png

0020_How_to_Schroedinger_from_Variation.png
see http://en.wikipedia.org/wiki/Functional_(mathematics)
Functional derivative http://en.wikipedia.org/wiki/Functional_derivative
also http://en.wikipedia.org/wiki/Functional_analysis
and http://en.wikipedia.org/wiki/History_of_variational_principles_in_physics
( Caution: some of these Wikipedia entries might be a bit "personal",
like e.g. the function
now in 2014 )
0030_Functional_derivative__Variation.png

0030_Functional_derivative__Variation.png
In Classical Mechanics - Newton equations can be re-obtained
from Lagrange equations;
but
it really becomes useful when the systems are complicated and described
by complicated
coordinates, as motion of beads attached to rails, motions limited by
tubes etc etc etc .....
Background at
http://en.wikipedia.org/wiki/Lagrangian_mechanics#Lagrange_equations_of_the_second_kind
The action integral http://en.wikipedia.org/wiki/Lagrangian_mechanics#Lagrangian_and_action
and http://en.wikipedia.org/wiki/Action_(physics)#Action_.28functional.29
For Schr. Eq. - this "principle" will be to find a suitable Functional
- and then finding a function which MINIMIZES that functional
and that will lead to the desired equation SO what is that
functional ( in the middle of the slide)
0040_Lagrange_Euler_Newton_Schroedinger.png
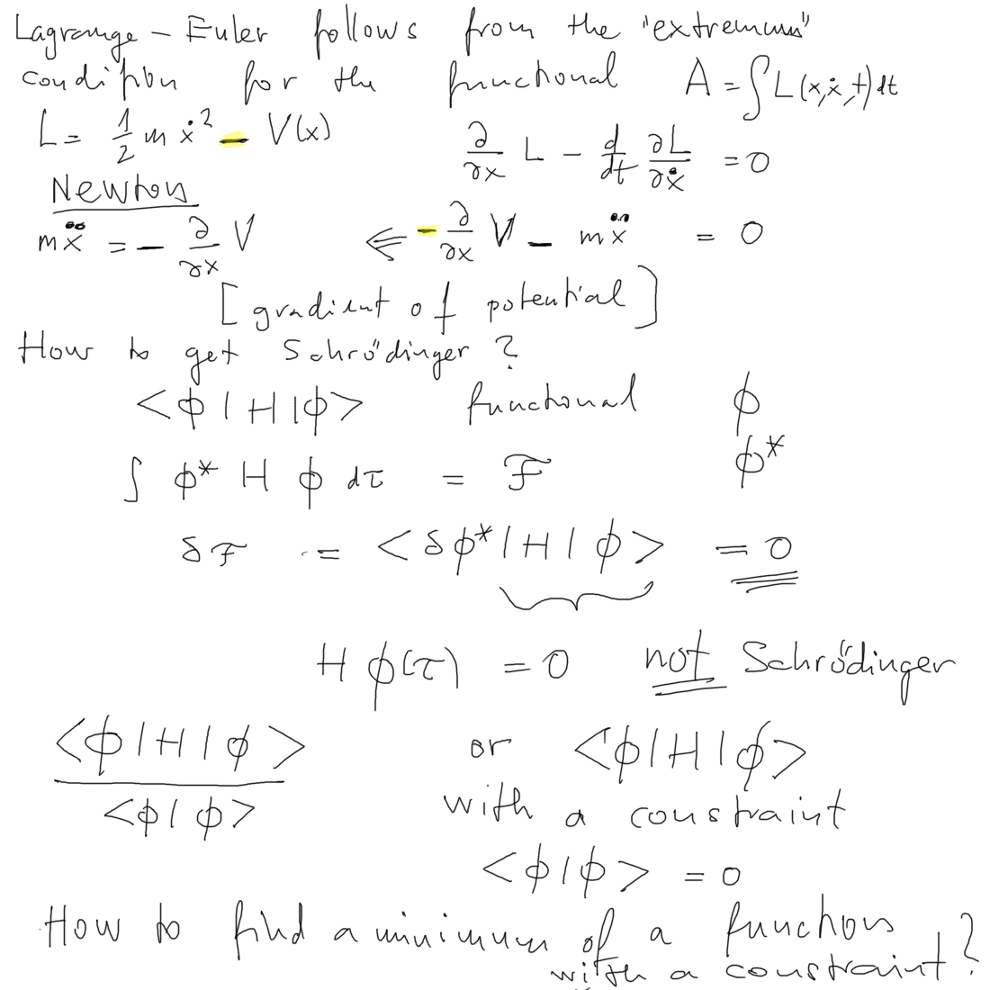
0040_Lagrange_Euler_Newton_Schroedinger.png
THIS IS NOT A WAY TO GET SCHRÖDINGER EQUATION - SEE
BELOW, not the right functional application
( but the expression is correct, it just needs one more thing,
MINIMUM WITH CONSTRAINT, i.e. extra condition )
MINIMUM WITH CONSTRAINT,
i.e. extra condition Lagrange
multipliers
http://en.wikipedia.org/wiki/Lagrange_multiplier
0050_Minimum_with_Constraint_Lagrange_Multiplier.png
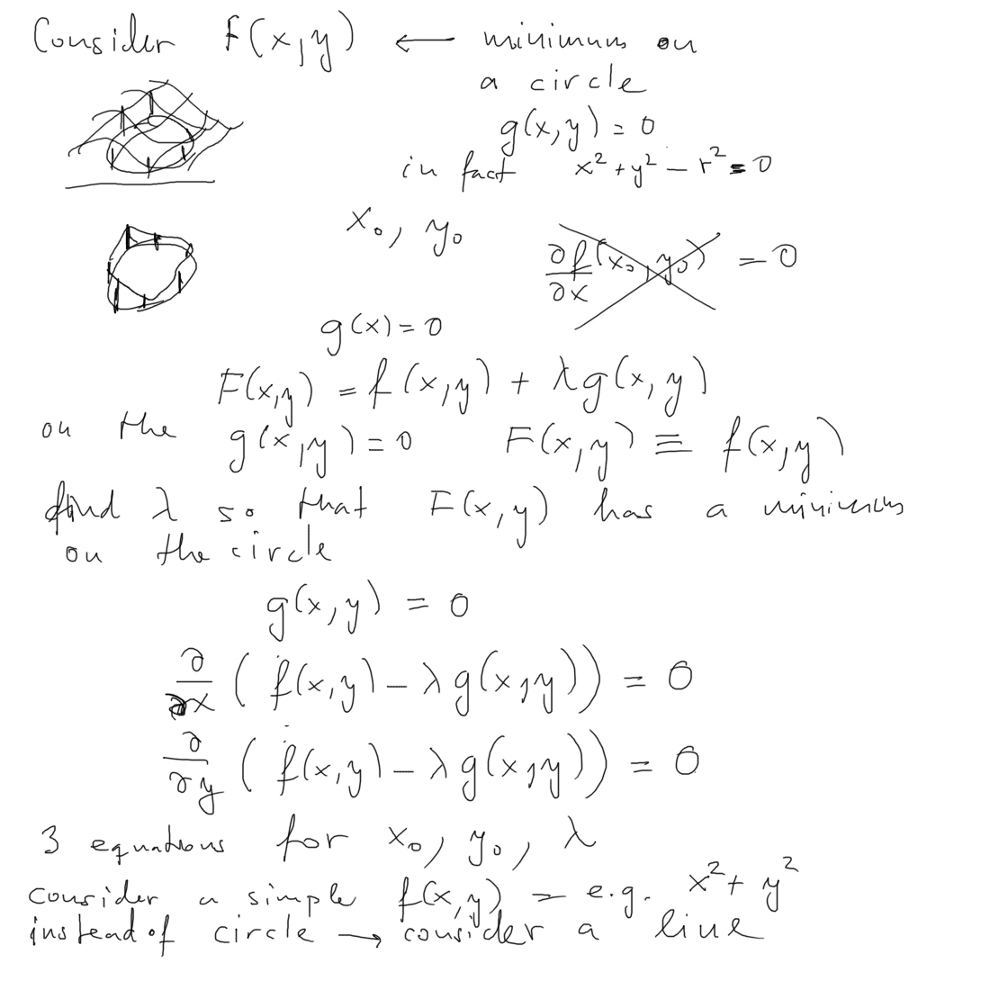
0050_Minimum_with_Constraint_Lagrange_Multiplier.png
MINIMUM WITH CONSTRAINT,
i.e. extra condition Lagrange
multipliers
http://en.wikipedia.org/wiki/Lagrange_multiplier
( example, minimum on a straight line instead of circle see also
this in last year ../2013_10_08/index.html
, xcf_004.png
and also year before ../2012_10_11/7_Minimum_with_Constraint-provides_Schroedinger.png
in ../2012_10_11/index.html
)
0060_Example_Minimum_Lagrange_Multiplier.png

0060_Example_Minimum_Lagrange_Multiplier.png
THIS IS the correct WAY TO
GET SCHRÖDINGER EQUATION
MINIMIZING THE EXPECTATION VALUE OF ENERGY
but applying MINIMUM WITH
CONSTRAINT, i.e. extra condition - The NORMALIZATION condition
RETURN to start of
variational discussion
In the
optimalization problem the
value of lambda is of no particular interest.
BUT for the Schrödinger equation lambda has the meaning of the
ENERGY, i.e. it is an important part.
0070_How_to_Schroedinger_from_Variation.png

0070_How_to_Schroedinger_from_Variation.png
RETURN to start of variational
discussion
NOW WE CAN APPLY THE SAME METHOD to the N-particle case, N-orbitals
One energy
expectation, N
orbitals,
N normalization conditions N Lagrange
Multipliers
0080_Concluding_Lagrange_Multipliers_Energies.png
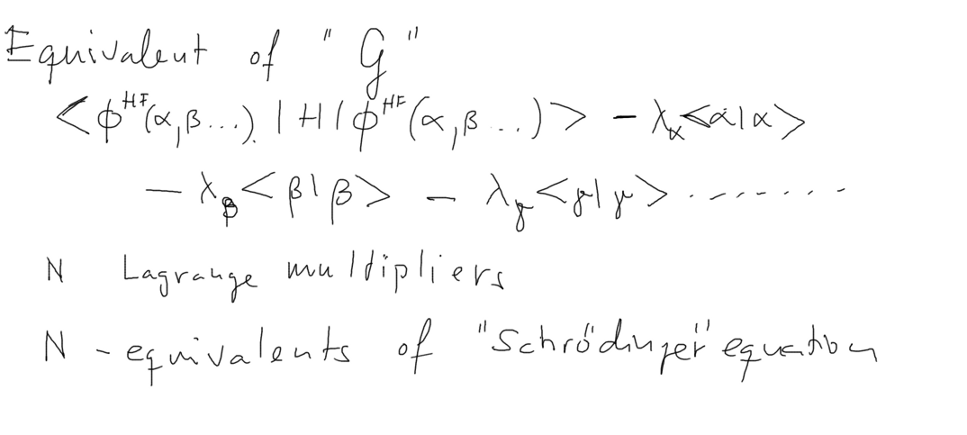
0080_Concluding_Lagrange_Multipliers_Energies.png
Using the outlined procedure we obtain the N equations
... which will look exactly as N Schr. Equations for N
orbitals
... but with the pecularity that
each of the equations (conditions) contains also all the other
orbitals
as outlined in the slide made after the lecture ....
Preview at the end of the lecture -- and -- Next time
Hartree-Fock-Preview.png

Hartree-Fock-Preview.png