PHYS261 - autumn 2014

to index 2014_09_23 Previous Lecture Note LECTURE NOTE 2014_09_25 2014_10_14 next lecture note

Many Electron Atoms - part 2

Evaluating expectation value of total H - similar purpose as in the He case:
it is t be used finally in a variational approach

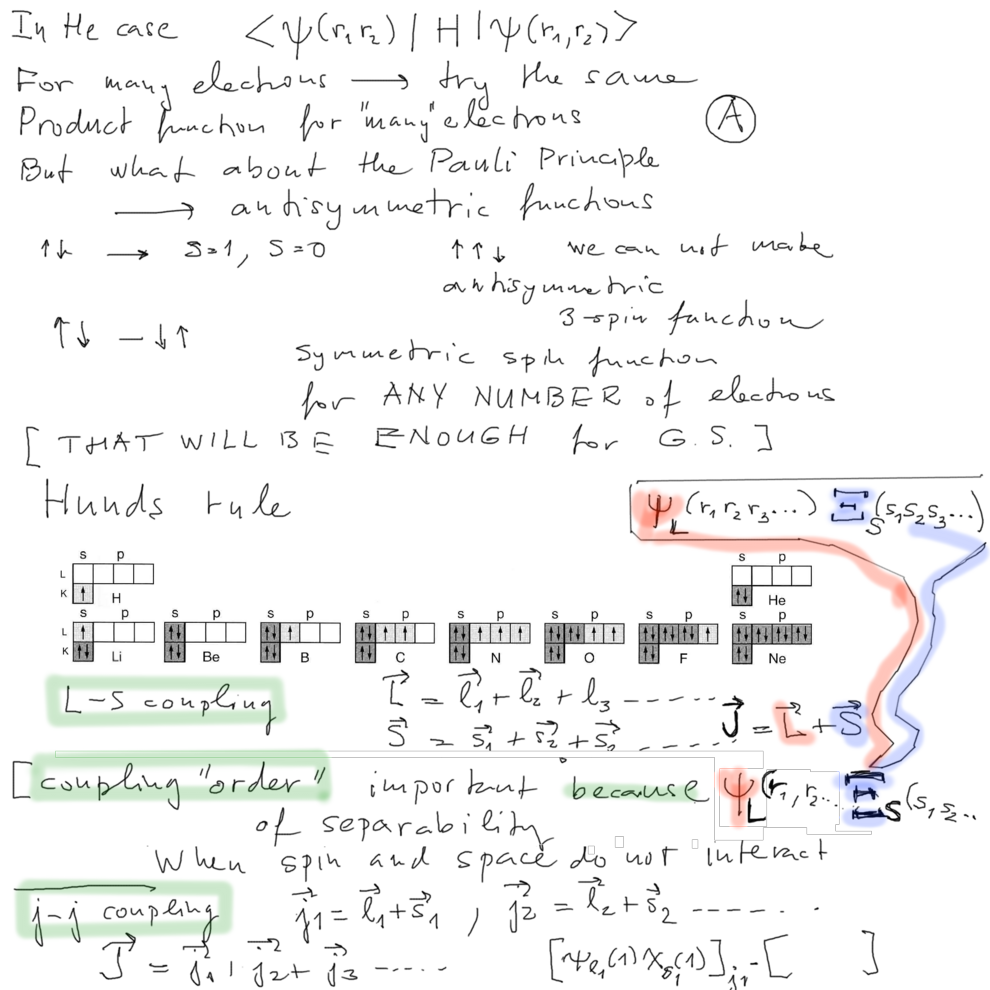
Using product function - where each electron placed in its orbital
(Pauli principle must be obeyed)
Generally the situation is more complicated for n > 2
because one can not make antisymmetric function of three spins

If we think that we allways work with j-j coupling, the situation is much simpler
( orbitals characterized by n,l, j and m of j - see the discussion further on )

Hund's rule: the levels are filled so that maximum spin S is achieved IN THE GROUND STATE
That means - the spin function is SYMMETRIC
which means the space function is antisymmetric   - THE REPULSION is weakest possible
                                       - the story of orthohelium once more -
    but in Hund's times this was not understood - therefore a special Hund's rule

xcf_0011.png

Hund's rule is historically important and popular in introductory texts:
                http://hyperphysics.phy-astr.gsu.edu/hbase/atomic/hund.html

More on L-S and j-j coupling - See the next board.

What does it mean that 2 angular momenta interact? Probably that the total energy of the system
depends       on          mutual    orientation     of the two   VECTORS -    i.e.   of their scalar product

H   =     H₀ +     J₁. J₂   where J₁   and J₂ are the 2 angular momenta H₀     is all the other energy

                                                                                   ( remember the effective spin-spin interaction, He ? )
      xcf_0020.png

xcf_0020.png

How to make antisymmetric (product) functions for N particles ( already N=2 and larger) ??
The answer:   REMEMBER THE DETERMINANTS - antrisymmetric property
permutations     ( http://en.wikipedia.org/wiki/Determinant )

      xcf_0025.png

xcf_0025.png

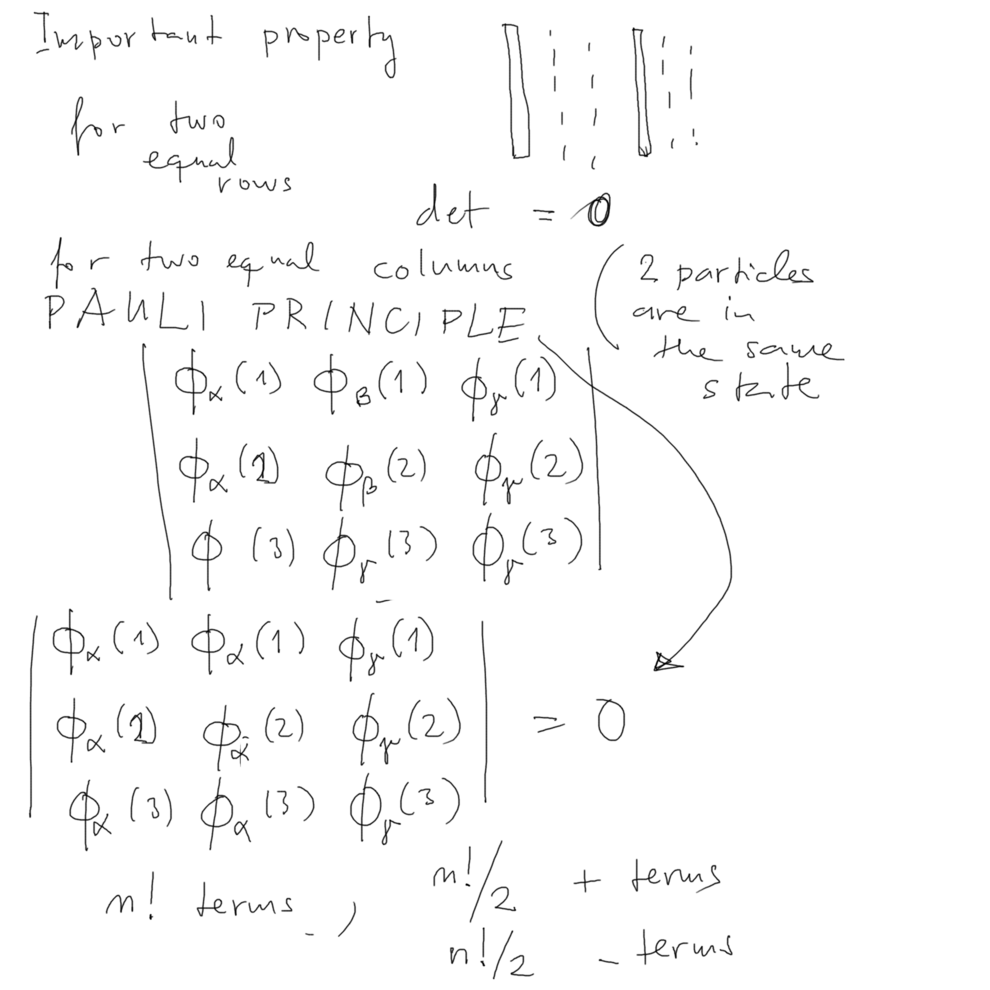
From the athematical definiton of the determinant - one property immediately leads back to PAULI:
NO TWO COLUMS CAN BE EQUAL - and no two rows can be equal
xcf_0029.png

xcf_0029.png
Look once more:
From the athematical definiton of the determinant - one property immediately leads back to PAULI:
NO TWO COLUMS CAN BE EQUAL - and no two rows can be equal
in our choice of notation no 2 columns IS RELEVANT

Normalization - there are N! terms - this gives the normalization factor each term gives 1
product with other terms gives 0 - thus ( one over squ

xcf_0032_Single_Particle_Operators.png

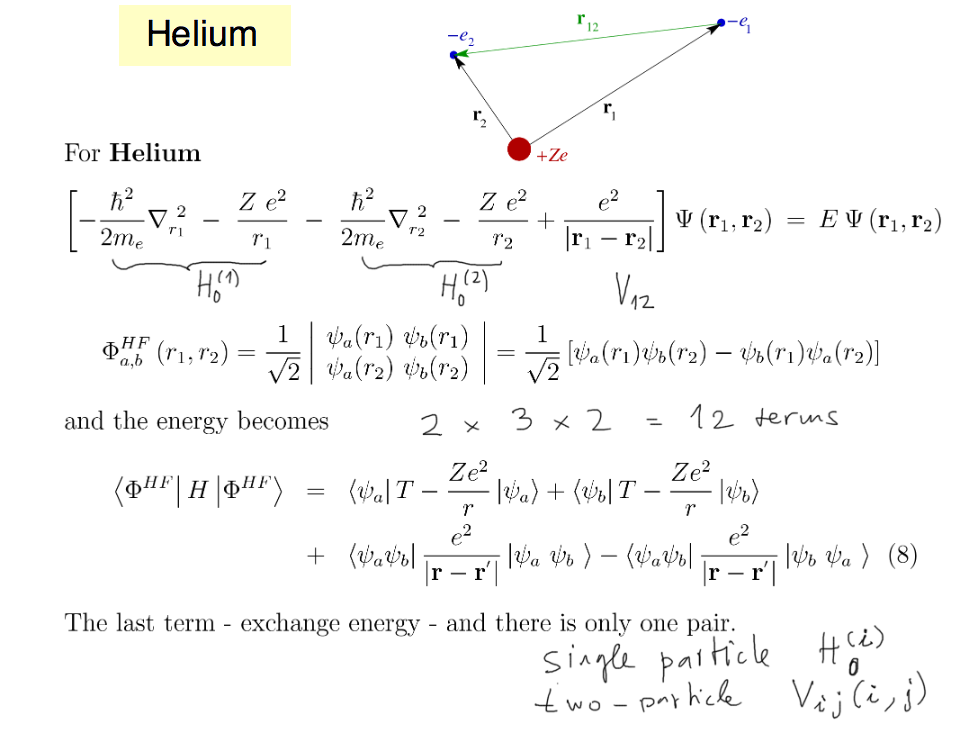
In the case of Helium, we already discussed this - how the terms get reduced in number (they are equal, and the normalization)

The discussion is reprinted below
xcf_0034_Helium.png

xcf_0034_Helium.png

xcf_0035_Lithium.png

nonzero-terms-Pair_interaction_operator.png

THIS IS REPRINTED FROM ../2014_09_18/index.html - discussion of exchange interaction in the Helium case
      jump BACK to the Helium - Lithium discussion
                    How does it go - the    2 times 3 times 2 = 12 terms become just 4 terms !
                    Look here - we did it at the whiteboard:
                    xcf_a050.png - from 28.09.2014
------------

xcf_a050.png - from 28.09.2014

The main aim of the present part is to prepare the variational method
- which in turn will lead to a
formal derivation of self-consistent field - SCF - method